Chaos and Complexity from Quantum Neural Network: A study with Diffusion Metric in Machine Learning

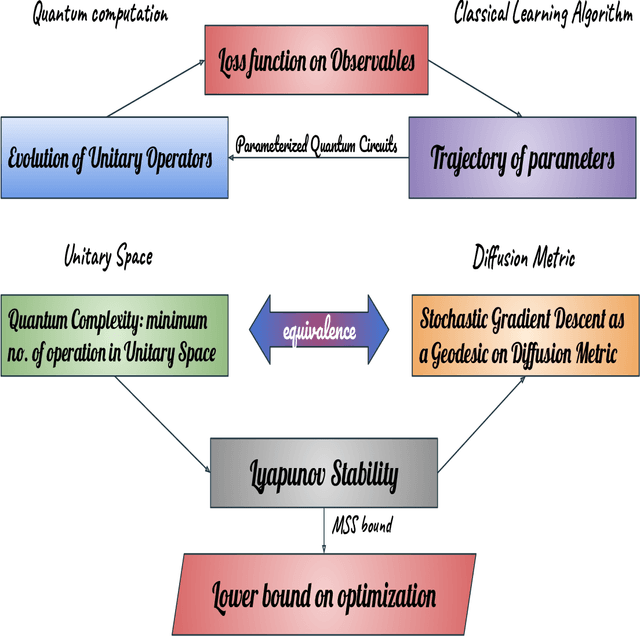
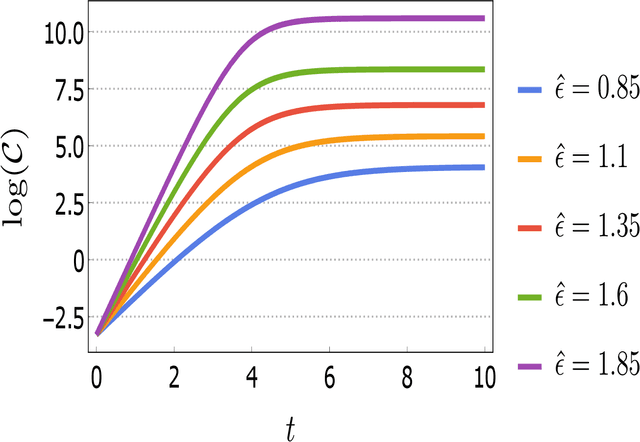
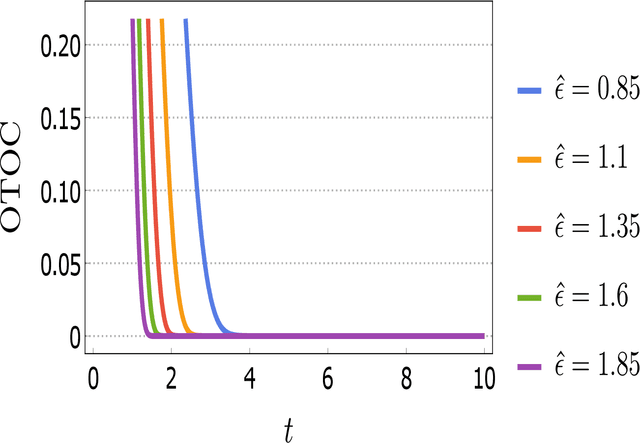
In this work, our prime objective is to study the phenomena of quantum chaos and complexity in the machine learning dynamics of Quantum Neural Network (QNN). A Parameterized Quantum Circuits (PQCs) in the hybrid quantum-classical framework is introduced as a universal function approximator to perform optimization with Stochastic Gradient Descent (SGD). We employ a statistical and differential geometric approach to study the learning theory of QNN. The evolution of parametrized unitary operators is correlated with the trajectory of parameters in the Diffusion metric. We establish the parametrized version of Quantum Complexity and Quantum Chaos in terms of physically relevant quantities, which are not only essential in determining the stability, but also essential in providing a very significant lower bound to the generalization capability of QNN. We explicitly prove that when the system executes limit cycles or oscillations in the phase space, the generalization capability of QNN is maximized. Moreover, a lower bound on the optimization rate is determined using the well known Maldacena Shenker Stanford (MSS) bound on the Quantum Lyapunov exponent.

Geometry Perspective Of Estimating Learning Capability Of Neural Networks

The paper uses statistical and differential geometric motivation to acquire prior information about the learning capability of an artificial neural network on a given dataset. The paper considers a broad class of neural networks with generalized architecture performing simple least square regression with stochastic gradient descent (SGD). The system characteristics at two critical epochs in the learning trajectory are analyzed. During some epochs of the training phase, the system reaches equilibrium with the generalization capability attaining a maximum. The system can also be coherent with localized, non-equilibrium states, which is characterized by the stabilization of the Hessian matrix. The paper proves that neural networks with higher generalization capability will have a slower convergence rate. The relationship between the generalization capability with the stability of the neural network has also been discussed. By correlating the principles of high-energy physics with the learning theory of neural networks, the paper establishes a variant of the Complexity-Action conjecture from an artificial neural network perspective.