Towards Knowledge Checking in Retrieval-augmented Generation: A Representation Perspective

Retrieval-Augmented Generation (RAG) systems have shown promise in enhancing the performance of Large Language Models (LLMs). However, these systems face challenges in effectively integrating external knowledge with the LLM's internal knowledge, often leading to issues with misleading or unhelpful information. This work aims to provide a systematic study on knowledge checking in RAG systems. We conduct a comprehensive analysis of LLM representation behaviors and demonstrate the significance of using representations in knowledge checking. Motivated by the findings, we further develop representation-based classifiers for knowledge filtering. We show substantial improvements in RAG performance, even when dealing with noisy knowledge databases. Our study provides new insights into leveraging LLM representations for enhancing the reliability and effectiveness of RAG systems.

AmazonQAC: A Large-Scale, Naturalistic Query Autocomplete Dataset

Query Autocomplete (QAC) is a critical feature in modern search engines, facilitating user interaction by predicting search queries based on input prefixes. Despite its widespread adoption, the absence of large-scale, realistic datasets has hindered advancements in QAC system development. This paper addresses this gap by introducing AmazonQAC, a new QAC dataset sourced from Amazon Search logs, comprising 395M samples. The dataset includes actual sequences of user-typed prefixes leading to final search terms, as well as session IDs and timestamps that support modeling the context-dependent aspects of QAC. We assess Prefix Trees, semantic retrieval, and Large Language Models (LLMs) with and without finetuning. We find that finetuned LLMs perform best, particularly when incorporating contextual information. However, even our best system achieves only half of what we calculate is theoretically possible on our test data, which implies QAC is a challenging problem that is far from solved with existing systems. This contribution aims to stimulate further research on QAC systems to better serve user needs in diverse environments. We open-source this data on Hugging Face at https://huggingface.co/datasets/amazon/AmazonQAC.

Dissipative Gradient Descent Ascent Method: A Control Theory Inspired Algorithm for Min-max Optimization

Gradient Descent Ascent (GDA) methods for min-max optimization problems typically produce oscillatory behavior that can lead to instability, e.g., in bilinear settings. To address this problem, we introduce a dissipation term into the GDA updates to dampen these oscillations. The proposed Dissipative GDA (DGDA) method can be seen as performing standard GDA on a state-augmented and regularized saddle function that does not strictly introduce additional convexity/concavity. We theoretically show the linear convergence of DGDA in the bilinear and strongly convex-strongly concave settings and assess its performance by comparing DGDA with other methods such as GDA, Extra-Gradient (EG), and Optimistic GDA. Our findings demonstrate that DGDA surpasses these methods, achieving superior convergence rates. We support our claims with two numerical examples that showcase DGDA's effectiveness in solving saddle point problems.

Constrained Reinforcement Learning via Dissipative Saddle Flow Dynamics

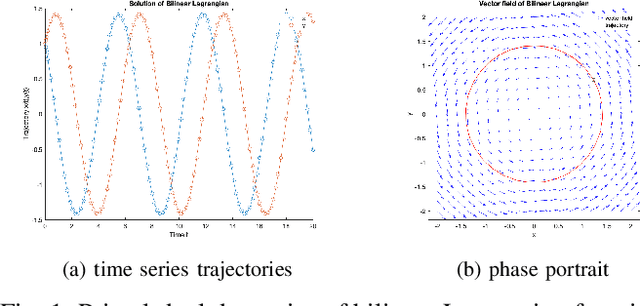
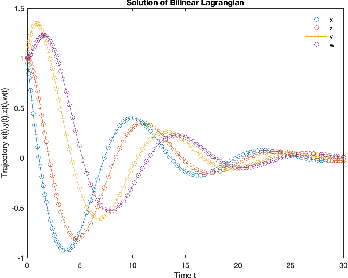
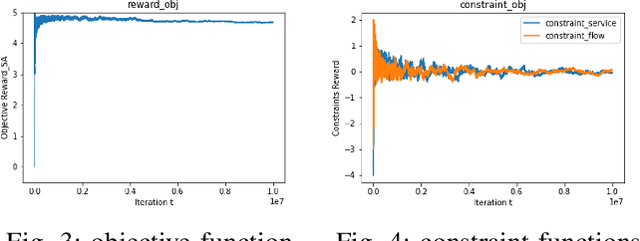
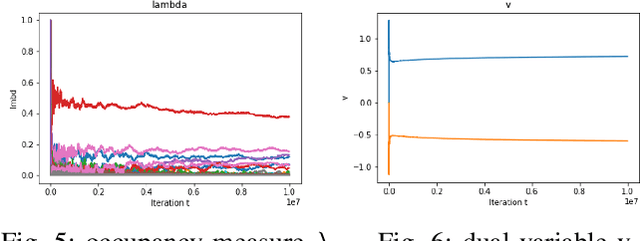
In constrained reinforcement learning (C-RL), an agent seeks to learn from the environment a policy that maximizes the expected cumulative reward while satisfying minimum requirements in secondary cumulative reward constraints. Several algorithms rooted in sampled-based primal-dual methods have been recently proposed to solve this problem in policy space. However, such methods are based on stochastic gradient descent ascent algorithms whose trajectories are connected to the optimal policy only after a mixing output stage that depends on the algorithm's history. As a result, there is a mismatch between the behavioral policy and the optimal one. In this work, we propose a novel algorithm for constrained RL that does not suffer from these limitations. Leveraging recent results on regularized saddle-flow dynamics, we develop a novel stochastic gradient descent-ascent algorithm whose trajectories converge to the optimal policy almost surely.