Constrained Reinforcement Learning via Dissipative Saddle Flow Dynamics
Paper and Code
Dec 03, 2022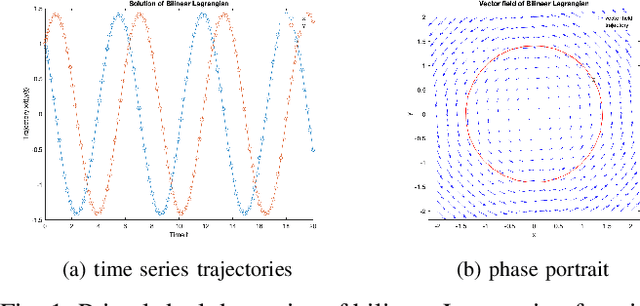
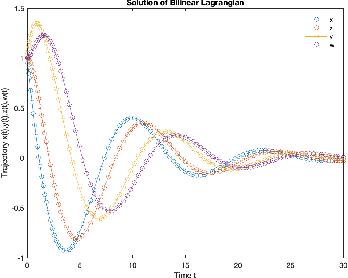
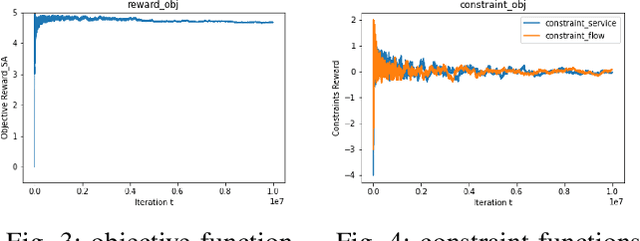
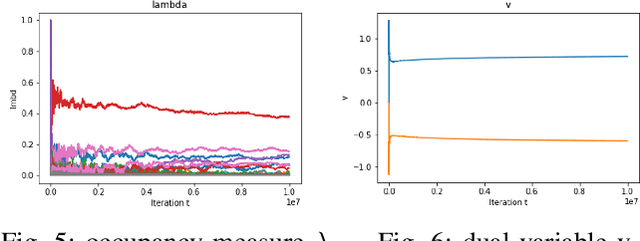
In constrained reinforcement learning (C-RL), an agent seeks to learn from the environment a policy that maximizes the expected cumulative reward while satisfying minimum requirements in secondary cumulative reward constraints. Several algorithms rooted in sampled-based primal-dual methods have been recently proposed to solve this problem in policy space. However, such methods are based on stochastic gradient descent ascent algorithms whose trajectories are connected to the optimal policy only after a mixing output stage that depends on the algorithm's history. As a result, there is a mismatch between the behavioral policy and the optimal one. In this work, we propose a novel algorithm for constrained RL that does not suffer from these limitations. Leveraging recent results on regularized saddle-flow dynamics, we develop a novel stochastic gradient descent-ascent algorithm whose trajectories converge to the optimal policy almost surely.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge