Enrique Mallada
Data-driven Acceleration of MPC with Guarantees
Nov 17, 2025Abstract:Model Predictive Control (MPC) is a powerful framework for optimal control but can be too slow for low-latency applications. We present a data-driven framework to accelerate MPC by replacing online optimization with a nonparametric policy constructed from offline MPC solutions. Our policy is greedy with respect to a constructed upper bound on the optimal cost-to-go, and can be implemented as a nonparametric lookup rule that is orders of magnitude faster than solving MPC online. Our analysis shows that under sufficient coverage condition of the offline data, the policy is recursively feasible and admits provable, bounded optimality gap. These conditions establish an explicit trade-off between the amount of data collected and the tightness of the bounds. Our experiments show that this policy is between 100 and 1000 times faster than standard MPC, with only a modest hit to optimality, showing potential for real-time control tasks.
A Local Polyak-Lojasiewicz and Descent Lemma of Gradient Descent For Overparametrized Linear Models
May 16, 2025Abstract:Most prior work on the convergence of gradient descent (GD) for overparameterized neural networks relies on strong assumptions on the step size (infinitesimal), the hidden-layer width (infinite), or the initialization (large, spectral, balanced). Recent efforts to relax these assumptions focus on two-layer linear networks trained with the squared loss. In this work, we derive a linear convergence rate for training two-layer linear neural networks with GD for general losses and under relaxed assumptions on the step size, width, and initialization. A key challenge in deriving this result is that classical ingredients for deriving convergence rates for nonconvex problems, such as the Polyak-{\L}ojasiewicz (PL) condition and Descent Lemma, do not hold globally for overparameterized neural networks. Here, we prove that these two conditions hold locally with local constants that depend on the weights. Then, we provide bounds on these local constants, which depend on the initialization of the weights, the current loss, and the global PL and smoothness constants of the non-overparameterized model. Based on these bounds, we derive a linear convergence rate for GD. Our convergence analysis not only improves upon prior results but also suggests a better choice for the step size, as verified through our numerical experiments.
Understanding the Learning Dynamics of LoRA: A Gradient Flow Perspective on Low-Rank Adaptation in Matrix Factorization
Mar 10, 2025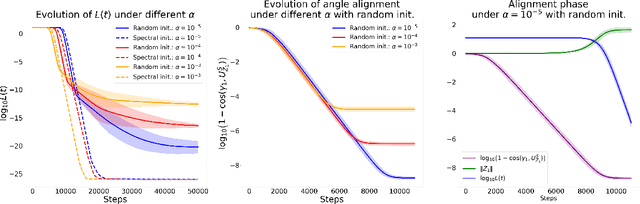
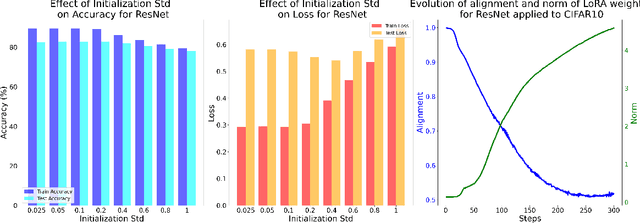
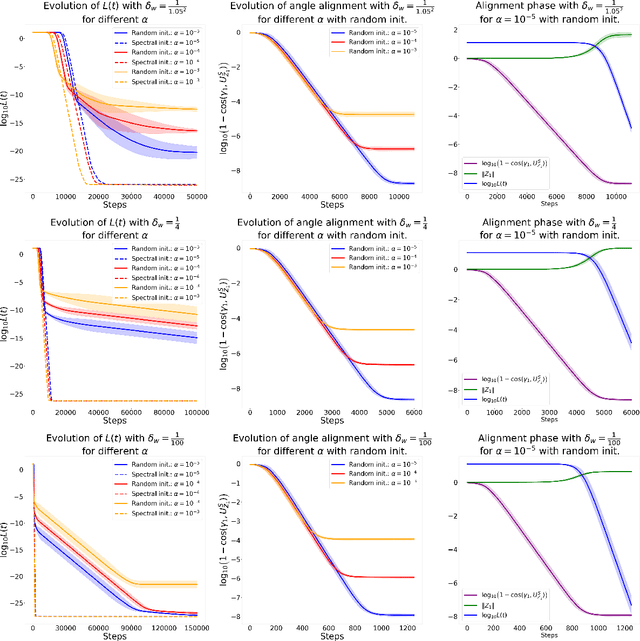
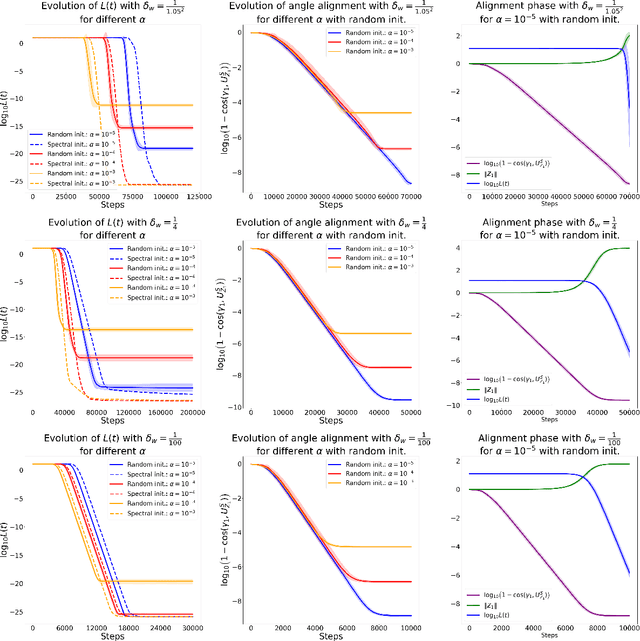
Abstract:Despite the empirical success of Low-Rank Adaptation (LoRA) in fine-tuning pre-trained models, there is little theoretical understanding of how first-order methods with carefully crafted initialization adapt models to new tasks. In this work, we take the first step towards bridging this gap by theoretically analyzing the learning dynamics of LoRA for matrix factorization (MF) under gradient flow (GF), emphasizing the crucial role of initialization. For small initialization, we theoretically show that GF converges to a neighborhood of the optimal solution, with smaller initialization leading to lower final error. Our analysis shows that the final error is affected by the misalignment between the singular spaces of the pre-trained model and the target matrix, and reducing the initialization scale improves alignment. To address this misalignment, we propose a spectral initialization for LoRA in MF and theoretically prove that GF with small spectral initialization converges to the fine-tuning task with arbitrary precision. Numerical experiments from MF and image classification validate our findings.
Variance-Aware Linear UCB with Deep Representation for Neural Contextual Bandits
Nov 08, 2024Abstract:By leveraging the representation power of deep neural networks, neural upper confidence bound (UCB) algorithms have shown success in contextual bandits. To further balance the exploration and exploitation, we propose Neural-$\sigma^2$-LinearUCB, a variance-aware algorithm that utilizes $\sigma^2_t$, i.e., an upper bound of the reward noise variance at round $t$, to enhance the uncertainty quantification quality of the UCB, resulting in a regret performance improvement. We provide an oracle version for our algorithm characterized by an oracle variance upper bound $\sigma^2_t$ and a practical version with a novel estimation for this variance bound. Theoretically, we provide rigorous regret analysis for both versions and prove that our oracle algorithm achieves a better regret guarantee than other neural-UCB algorithms in the neural contextual bandits setting. Empirically, our practical method enjoys a similar computational efficiency, while outperforming state-of-the-art techniques by having a better calibration and lower regret across multiple standard settings, including on the synthetic, UCI, MNIST, and CIFAR-10 datasets.
Invertibility of Discrete-Time Linear Systems with Sparse Inputs
Mar 29, 2024Abstract:One of the fundamental problems of interest for discrete-time linear systems is whether its input sequence may be recovered given its output sequence, a.k.a. the left inversion problem. Many conditions on the state space geometry, dynamics, and spectral structure of a system have been used to characterize the well-posedness of this problem, without assumptions on the inputs. However, certain structural assumptions, such as input sparsity, have been shown to translate to practical gains in the performance of inversion algorithms, surpassing classical guarantees. Establishing necessary and sufficient conditions for left invertibility of systems with sparse inputs is therefore a crucial step toward understanding the performance limits of system inversion under structured input assumptions. In this work, we provide the first necessary and sufficient characterizations of left invertibility for linear systems with sparse inputs, echoing classic characterizations for standard linear systems. The key insight in deriving these results is in establishing the existence of two novel geometric invariants unique to the sparse-input setting, the weakly unobservable and strongly reachable subspace arrangements. By means of a concrete example, we demonstrate the utility of these characterizations. We conclude by discussing extensions and applications of this framework to several related problems in sparse control.
Dissipative Gradient Descent Ascent Method: A Control Theory Inspired Algorithm for Min-max Optimization
Mar 14, 2024Abstract:Gradient Descent Ascent (GDA) methods for min-max optimization problems typically produce oscillatory behavior that can lead to instability, e.g., in bilinear settings. To address this problem, we introduce a dissipation term into the GDA updates to dampen these oscillations. The proposed Dissipative GDA (DGDA) method can be seen as performing standard GDA on a state-augmented and regularized saddle function that does not strictly introduce additional convexity/concavity. We theoretically show the linear convergence of DGDA in the bilinear and strongly convex-strongly concave settings and assess its performance by comparing DGDA with other methods such as GDA, Extra-Gradient (EG), and Optimistic GDA. Our findings demonstrate that DGDA surpasses these methods, achieving superior convergence rates. We support our claims with two numerical examples that showcase DGDA's effectiveness in solving saddle point problems.
Learning safety critics via a non-contractive binary bellman operator
Jan 23, 2024Abstract:The inability to naturally enforce safety in Reinforcement Learning (RL), with limited failures, is a core challenge impeding its use in real-world applications. One notion of safety of vast practical relevance is the ability to avoid (unsafe) regions of the state space. Though such a safety goal can be captured by an action-value-like function, a.k.a. safety critics, the associated operator lacks the desired contraction and uniqueness properties that the classical Bellman operator enjoys. In this work, we overcome the non-contractiveness of safety critic operators by leveraging that safety is a binary property. To that end, we study the properties of the binary safety critic associated with a deterministic dynamical system that seeks to avoid reaching an unsafe region. We formulate the corresponding binary Bellman equation (B2E) for safety and study its properties. While the resulting operator is still non-contractive, we fully characterize its fixed points representing--except for a spurious solution--maximal persistently safe regions of the state space that can always avoid failure. We provide an algorithm that, by design, leverages axiomatic knowledge of safe data to avoid spurious fixed points.
Early Neuron Alignment in Two-layer ReLU Networks with Small Initialization
Jul 24, 2023Abstract:This paper studies the problem of training a two-layer ReLU network for binary classification using gradient flow with small initialization. We consider a training dataset with well-separated input vectors: Any pair of input data with the same label are positively correlated, and any pair with different labels are negatively correlated. Our analysis shows that, during the early phase of training, neurons in the first layer try to align with either the positive data or the negative data, depending on its corresponding weight on the second layer. A careful analysis of the neurons' directional dynamics allows us to provide an $\mathcal{O}(\frac{\log n}{\sqrt{\mu}})$ upper bound on the time it takes for all neurons to achieve good alignment with the input data, where $n$ is the number of data points and $\mu$ measures how well the data are separated. After the early alignment phase, the loss converges to zero at a $\mathcal{O}(\frac{1}{t})$ rate, and the weight matrix on the first layer is approximately low-rank. Numerical experiments on the MNIST dataset illustrate our theoretical findings.
Constrained Reinforcement Learning via Dissipative Saddle Flow Dynamics
Dec 03, 2022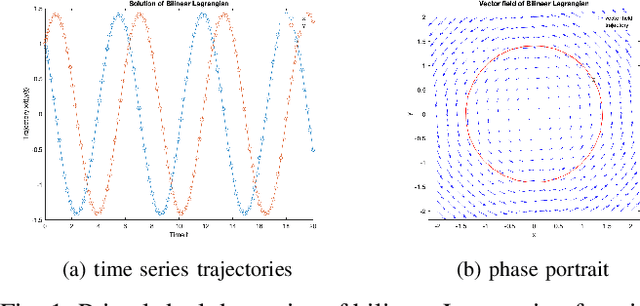
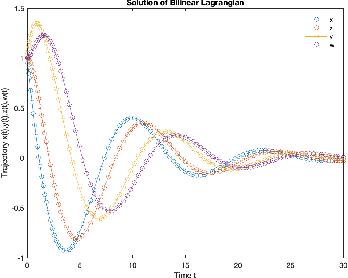
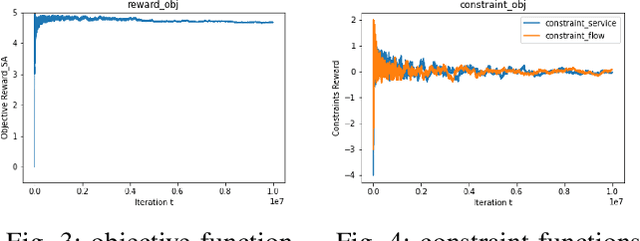
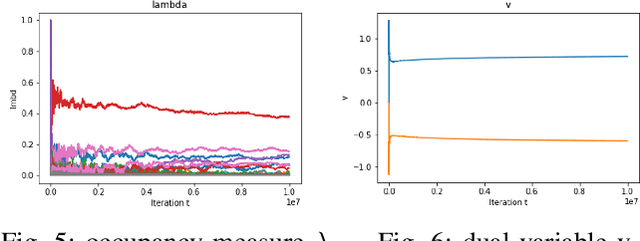
Abstract:In constrained reinforcement learning (C-RL), an agent seeks to learn from the environment a policy that maximizes the expected cumulative reward while satisfying minimum requirements in secondary cumulative reward constraints. Several algorithms rooted in sampled-based primal-dual methods have been recently proposed to solve this problem in policy space. However, such methods are based on stochastic gradient descent ascent algorithms whose trajectories are connected to the optimal policy only after a mixing output stage that depends on the algorithm's history. As a result, there is a mismatch between the behavioral policy and the optimal one. In this work, we propose a novel algorithm for constrained RL that does not suffer from these limitations. Leveraging recent results on regularized saddle-flow dynamics, we develop a novel stochastic gradient descent-ascent algorithm whose trajectories converge to the optimal policy almost surely.
Learning Coherent Clusters in Weakly-Connected Network Systems
Nov 28, 2022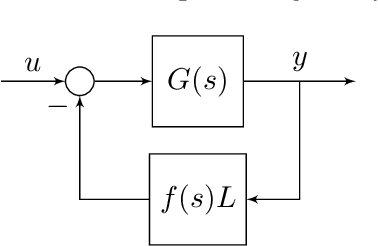
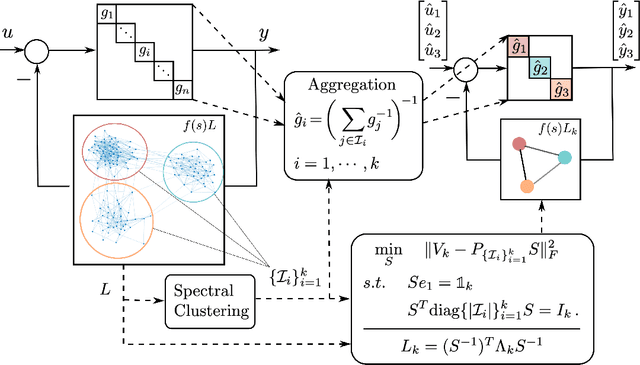
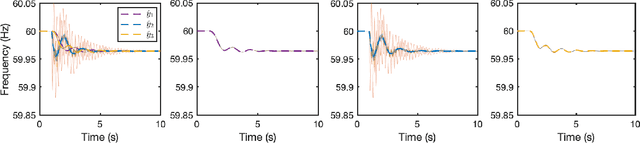
Abstract:We propose a structure-preserving model-reduction methodology for large-scale dynamic networks with tightly-connected components. First, the coherent groups are identified by a spectral clustering algorithm on the graph Laplacian matrix that models the network feedback. Then, a reduced network is built, where each node represents the aggregate dynamics of each coherent group, and the reduced network captures the dynamic coupling between the groups. We provide an upper bound on the approximation error when the network graph is randomly generated from a weight stochastic block model. Finally, numerical experiments align with and validate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge