Hancheng Min
A Local Polyak-Lojasiewicz and Descent Lemma of Gradient Descent For Overparametrized Linear Models
May 16, 2025Abstract:Most prior work on the convergence of gradient descent (GD) for overparameterized neural networks relies on strong assumptions on the step size (infinitesimal), the hidden-layer width (infinite), or the initialization (large, spectral, balanced). Recent efforts to relax these assumptions focus on two-layer linear networks trained with the squared loss. In this work, we derive a linear convergence rate for training two-layer linear neural networks with GD for general losses and under relaxed assumptions on the step size, width, and initialization. A key challenge in deriving this result is that classical ingredients for deriving convergence rates for nonconvex problems, such as the Polyak-{\L}ojasiewicz (PL) condition and Descent Lemma, do not hold globally for overparameterized neural networks. Here, we prove that these two conditions hold locally with local constants that depend on the weights. Then, we provide bounds on these local constants, which depend on the initialization of the weights, the current loss, and the global PL and smoothness constants of the non-overparameterized model. Based on these bounds, we derive a linear convergence rate for GD. Our convergence analysis not only improves upon prior results but also suggests a better choice for the step size, as verified through our numerical experiments.
Concept Lancet: Image Editing with Compositional Representation Transplant
Apr 03, 2025Abstract:Diffusion models are widely used for image editing tasks. Existing editing methods often design a representation manipulation procedure by curating an edit direction in the text embedding or score space. However, such a procedure faces a key challenge: overestimating the edit strength harms visual consistency while underestimating it fails the editing task. Notably, each source image may require a different editing strength, and it is costly to search for an appropriate strength via trial-and-error. To address this challenge, we propose Concept Lancet (CoLan), a zero-shot plug-and-play framework for principled representation manipulation in diffusion-based image editing. At inference time, we decompose the source input in the latent (text embedding or diffusion score) space as a sparse linear combination of the representations of the collected visual concepts. This allows us to accurately estimate the presence of concepts in each image, which informs the edit. Based on the editing task (replace/add/remove), we perform a customized concept transplant process to impose the corresponding editing direction. To sufficiently model the concept space, we curate a conceptual representation dataset, CoLan-150K, which contains diverse descriptions and scenarios of visual terms and phrases for the latent dictionary. Experiments on multiple diffusion-based image editing baselines show that methods equipped with CoLan achieve state-of-the-art performance in editing effectiveness and consistency preservation.
Understanding the Learning Dynamics of LoRA: A Gradient Flow Perspective on Low-Rank Adaptation in Matrix Factorization
Mar 10, 2025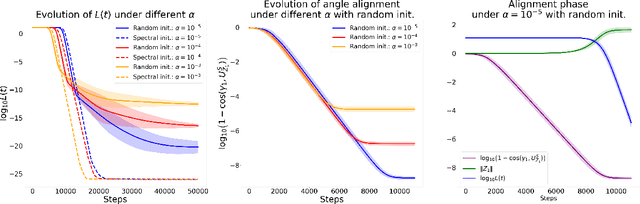
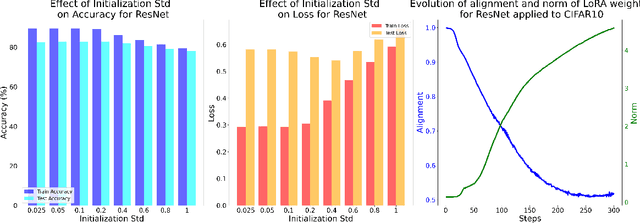
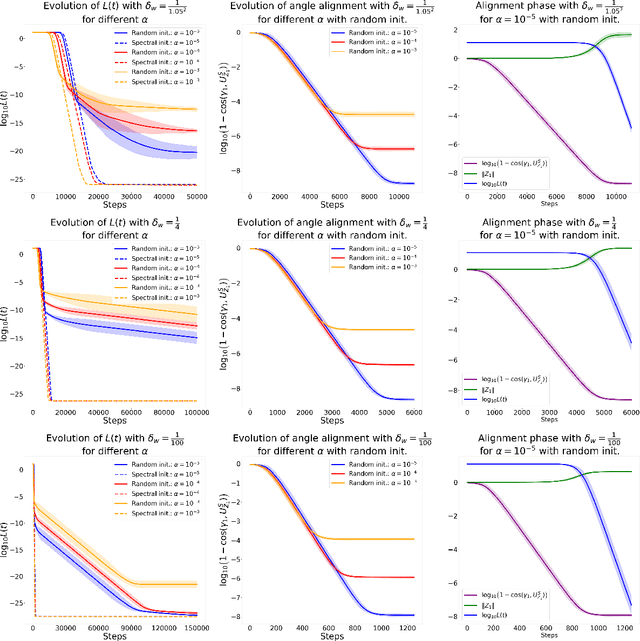
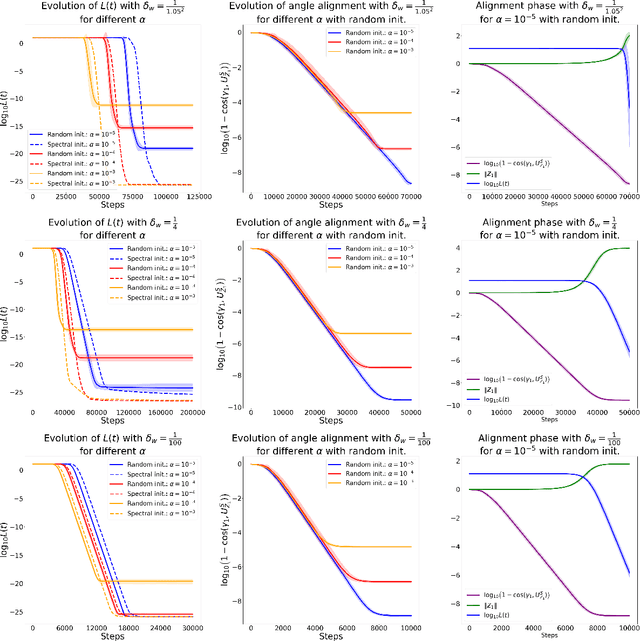
Abstract:Despite the empirical success of Low-Rank Adaptation (LoRA) in fine-tuning pre-trained models, there is little theoretical understanding of how first-order methods with carefully crafted initialization adapt models to new tasks. In this work, we take the first step towards bridging this gap by theoretically analyzing the learning dynamics of LoRA for matrix factorization (MF) under gradient flow (GF), emphasizing the crucial role of initialization. For small initialization, we theoretically show that GF converges to a neighborhood of the optimal solution, with smaller initialization leading to lower final error. Our analysis shows that the final error is affected by the misalignment between the singular spaces of the pre-trained model and the target matrix, and reducing the initialization scale improves alignment. To address this misalignment, we propose a spectral initialization for LoRA in MF and theoretically prove that GF with small spectral initialization converges to the fine-tuning task with arbitrary precision. Numerical experiments from MF and image classification validate our findings.
Can Implicit Bias Imply Adversarial Robustness?
May 24, 2024Abstract:The implicit bias of gradient-based training algorithms has been considered mostly beneficial as it leads to trained networks that often generalize well. However, Frei et al. (2023) show that such implicit bias can harm adversarial robustness. Specifically, when the data consists of clusters with small inter-cluster correlation, a shallow (two-layer) ReLU network trained by gradient flow generalizes well, but it is not robust to adversarial attacks of small radius, despite the existence of a much more robust classifier that can be explicitly constructed from a shallow network. In this paper, we extend recent analyses of neuron alignment to show that a shallow network with a polynomial ReLU activation (pReLU) trained by gradient flow not only generalizes well but is also robust to adversarial attacks. Our results highlight the importance of the interplay between data structure and architecture design in the implicit bias and robustness of trained networks.
Learning safety critics via a non-contractive binary bellman operator
Jan 23, 2024Abstract:The inability to naturally enforce safety in Reinforcement Learning (RL), with limited failures, is a core challenge impeding its use in real-world applications. One notion of safety of vast practical relevance is the ability to avoid (unsafe) regions of the state space. Though such a safety goal can be captured by an action-value-like function, a.k.a. safety critics, the associated operator lacks the desired contraction and uniqueness properties that the classical Bellman operator enjoys. In this work, we overcome the non-contractiveness of safety critic operators by leveraging that safety is a binary property. To that end, we study the properties of the binary safety critic associated with a deterministic dynamical system that seeks to avoid reaching an unsafe region. We formulate the corresponding binary Bellman equation (B2E) for safety and study its properties. While the resulting operator is still non-contractive, we fully characterize its fixed points representing--except for a spurious solution--maximal persistently safe regions of the state space that can always avoid failure. We provide an algorithm that, by design, leverages axiomatic knowledge of safe data to avoid spurious fixed points.
Early Neuron Alignment in Two-layer ReLU Networks with Small Initialization
Jul 24, 2023Abstract:This paper studies the problem of training a two-layer ReLU network for binary classification using gradient flow with small initialization. We consider a training dataset with well-separated input vectors: Any pair of input data with the same label are positively correlated, and any pair with different labels are negatively correlated. Our analysis shows that, during the early phase of training, neurons in the first layer try to align with either the positive data or the negative data, depending on its corresponding weight on the second layer. A careful analysis of the neurons' directional dynamics allows us to provide an $\mathcal{O}(\frac{\log n}{\sqrt{\mu}})$ upper bound on the time it takes for all neurons to achieve good alignment with the input data, where $n$ is the number of data points and $\mu$ measures how well the data are separated. After the early alignment phase, the loss converges to zero at a $\mathcal{O}(\frac{1}{t})$ rate, and the weight matrix on the first layer is approximately low-rank. Numerical experiments on the MNIST dataset illustrate our theoretical findings.
Learning Coherent Clusters in Weakly-Connected Network Systems
Nov 28, 2022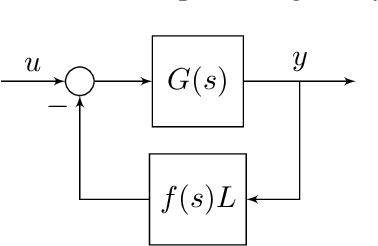
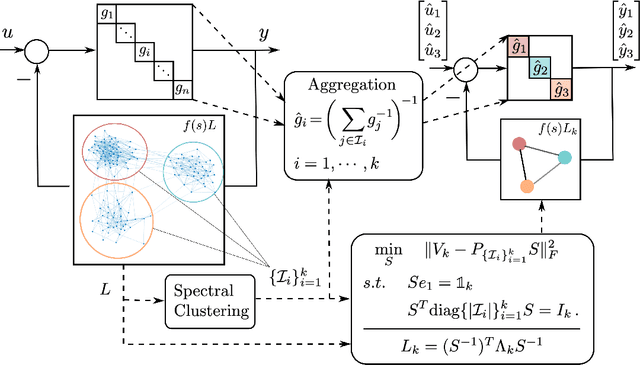
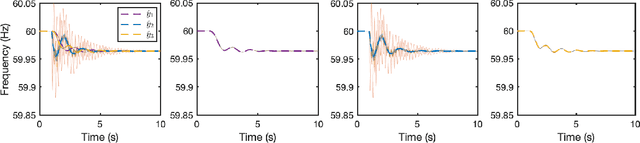
Abstract:We propose a structure-preserving model-reduction methodology for large-scale dynamic networks with tightly-connected components. First, the coherent groups are identified by a spectral clustering algorithm on the graph Laplacian matrix that models the network feedback. Then, a reduced network is built, where each node represents the aggregate dynamics of each coherent group, and the reduced network captures the dynamic coupling between the groups. We provide an upper bound on the approximation error when the network graph is randomly generated from a weight stochastic block model. Finally, numerical experiments align with and validate our theoretical findings.
Reinforcement Learning with Almost Sure Constraints
Dec 09, 2021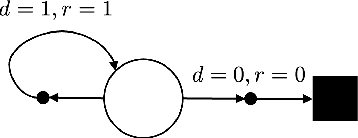
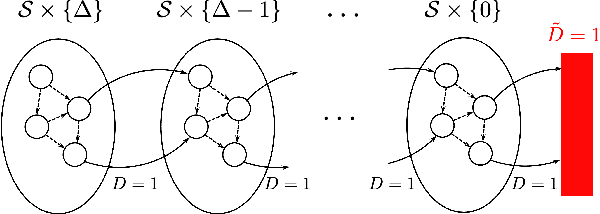
Abstract:In this work we address the problem of finding feasible policies for Constrained Markov Decision Processes under probability one constraints. We argue that stationary policies are not sufficient for solving this problem, and that a rich class of policies can be found by endowing the controller with a scalar quantity, so called budget, that tracks how close the agent is to violating the constraint. We show that the minimal budget required to act safely can be obtained as the smallest fixed point of a Bellman-like operator, for which we analyze its convergence properties. We also show how to learn this quantity when the true kernel of the Markov decision process is not known, while providing sample-complexity bounds. The utility of knowing this minimal budget relies in that it can aid in the search of optimal or near-optimal policies by shrinking down the region of the state space the agent must navigate. Simulations illustrate the different nature of probability one constraints against the typically used constraints in expectation.
Learning to Act Safely with Limited Exposure and Almost Sure Certainty
May 25, 2021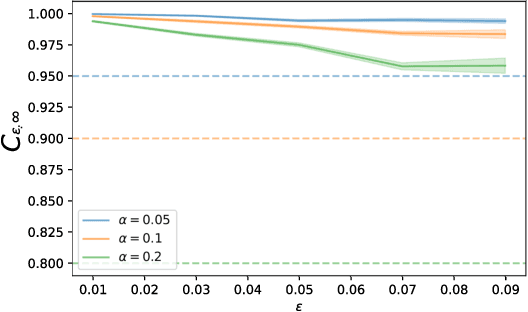
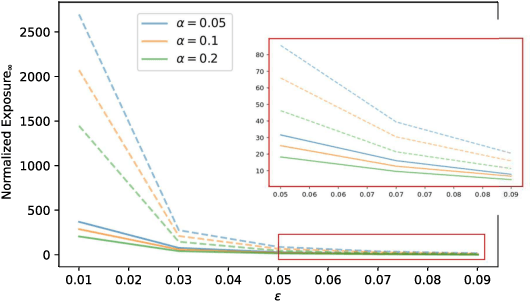
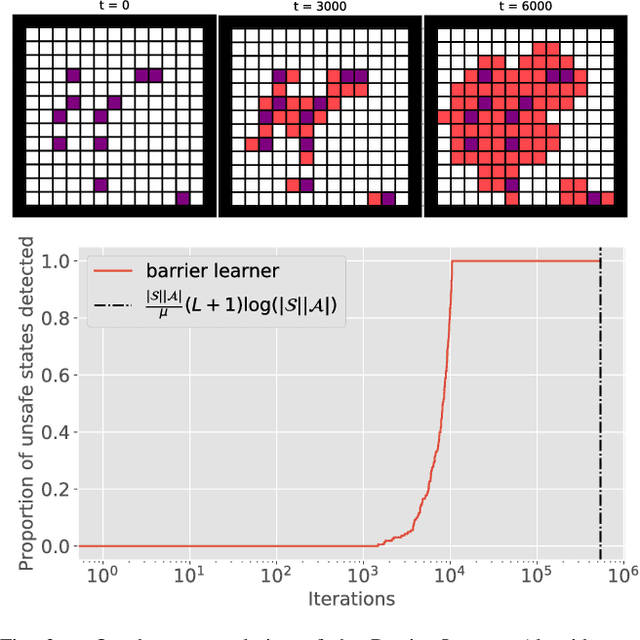

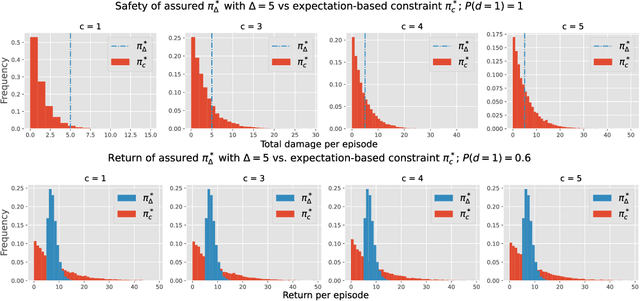
Abstract:This paper aims to put forward the concept that learning to take safe actions in unknown environments, even with probability one guarantees, can be achieved without the need for an unbounded number of exploratory trials, provided that one is willing to navigate trade-offs between optimality, level of exposure to unsafe events, and the maximum detection time of unsafe actions. We illustrate this concept in two complementary settings. We first focus on the canonical multi-armed bandit problem and seek to study the intrinsic trade-offs of learning safety in the presence of uncertainty. Under mild assumptions on sufficient exploration, we provide an algorithm that provably detects all unsafe machines in an (expected) finite number of rounds. The analysis also unveils a trade-off between the number of rounds needed to secure the environment and the probability of discarding safe machines. We then consider the problem of finding optimal policies for a Markov Decision Process (MDP) with almost sure constraints. We show that the (action) value function satisfies a barrier-based decomposition which allows for the identification of feasible policies independently of the reward process. Using this decomposition, we develop a Barrier-learning algorithm, that identifies such unsafe state-action pairs in a finite expected number of steps. Our analysis further highlights a trade-off between the time lag for the underlying MDP necessary to detect unsafe actions, and the level of exposure to unsafe events. Simulations corroborate our theoretical findings, further illustrating the aforementioned trade-offs, and suggesting that safety constraints can further speed up the learning process.
On the Explicit Role of Initialization on the Convergence and Implicit Bias of Overparametrized Linear Networks
May 13, 2021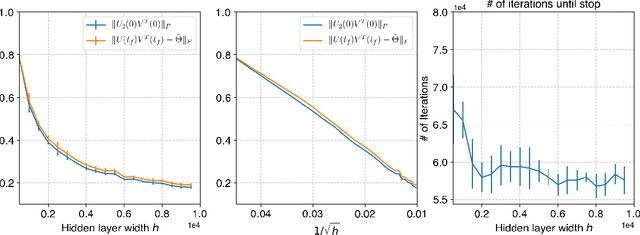
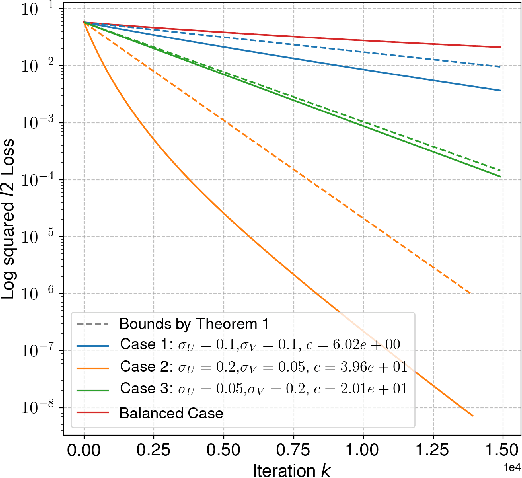
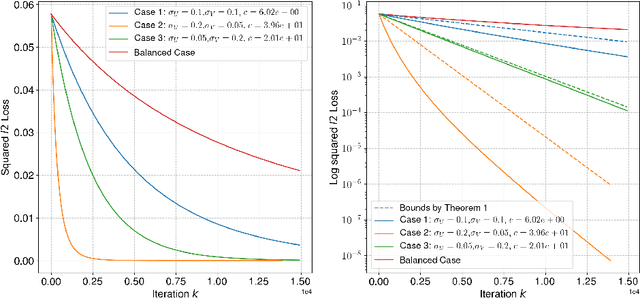
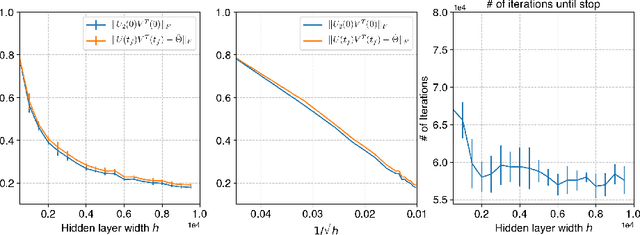
Abstract:Neural networks trained via gradient descent with random initialization and without any regularization enjoy good generalization performance in practice despite being highly overparametrized. A promising direction to explain this phenomenon is to study how initialization and overparametrization affect convergence and implicit bias of training algorithms. In this paper, we present a novel analysis of single-hidden-layer linear networks trained under gradient flow, which connects initialization, optimization, and overparametrization. Firstly, we show that the squared loss converges exponentially to its optimum at a rate that depends on the level of imbalance of the initialization. Secondly, we show that proper initialization constrains the dynamics of the network parameters to lie within an invariant set. In turn, minimizing the loss over this set leads to the min-norm solution. Finally, we show that large hidden layer width, together with (properly scaled) random initialization, ensures proximity to such an invariant set during training, allowing us to derive a novel non-asymptotic upper-bound on the distance between the trained network and the min-norm solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge