Learning Coherent Clusters in Weakly-Connected Network Systems
Paper and Code
Nov 28, 2022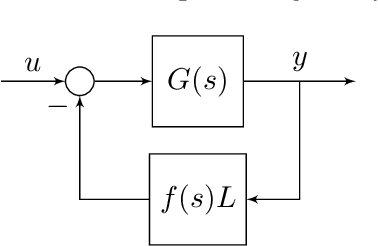
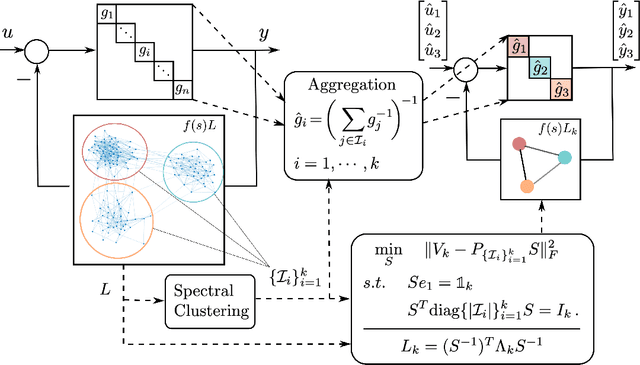
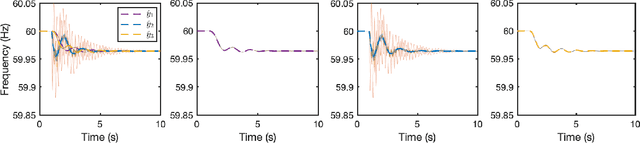
We propose a structure-preserving model-reduction methodology for large-scale dynamic networks with tightly-connected components. First, the coherent groups are identified by a spectral clustering algorithm on the graph Laplacian matrix that models the network feedback. Then, a reduced network is built, where each node represents the aggregate dynamics of each coherent group, and the reduced network captures the dynamic coupling between the groups. We provide an upper bound on the approximation error when the network graph is randomly generated from a weight stochastic block model. Finally, numerical experiments align with and validate our theoretical findings.
* arXiv admin note: text overlap with arXiv:2209.13701
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge