Understanding the Learning Dynamics of LoRA: A Gradient Flow Perspective on Low-Rank Adaptation in Matrix Factorization

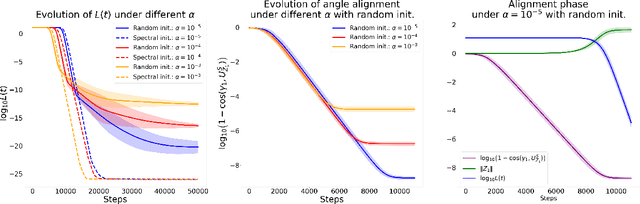
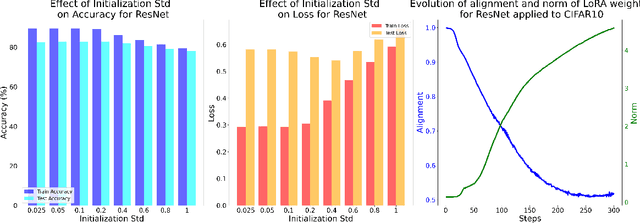
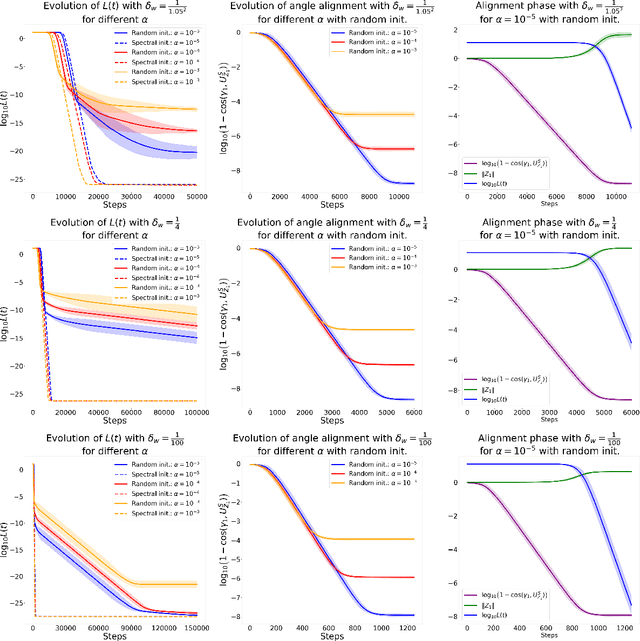
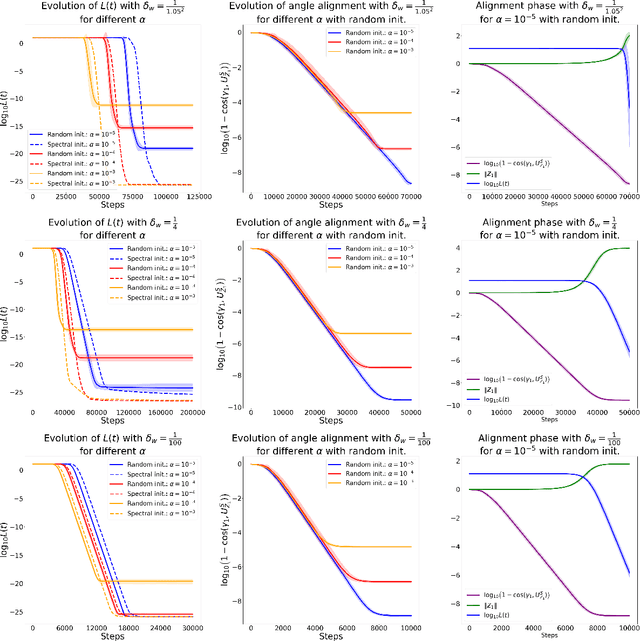
Despite the empirical success of Low-Rank Adaptation (LoRA) in fine-tuning pre-trained models, there is little theoretical understanding of how first-order methods with carefully crafted initialization adapt models to new tasks. In this work, we take the first step towards bridging this gap by theoretically analyzing the learning dynamics of LoRA for matrix factorization (MF) under gradient flow (GF), emphasizing the crucial role of initialization. For small initialization, we theoretically show that GF converges to a neighborhood of the optimal solution, with smaller initialization leading to lower final error. Our analysis shows that the final error is affected by the misalignment between the singular spaces of the pre-trained model and the target matrix, and reducing the initialization scale improves alignment. To address this misalignment, we propose a spectral initialization for LoRA in MF and theoretically prove that GF with small spectral initialization converges to the fine-tuning task with arbitrary precision. Numerical experiments from MF and image classification validate our findings.

D'OH: Decoder-Only random Hypernetworks for Implicit Neural Representations

Deep implicit functions have been found to be an effective tool for efficiently encoding all manner of natural signals. Their attractiveness stems from their ability to compactly represent signals with little to no off-line training data. Instead, they leverage the implicit bias of deep networks to decouple hidden redundancies within the signal. In this paper, we explore the hypothesis that additional compression can be achieved by leveraging the redundancies that exist between layers. We propose to use a novel run-time decoder-only hypernetwork - that uses no offline training data - to better model this cross-layer parameter redundancy. Previous applications of hyper-networks with deep implicit functions have applied feed-forward encoder/decoder frameworks that rely on large offline datasets that do not generalize beyond the signals they were trained on. We instead present a strategy for the initialization of run-time deep implicit functions for single-instance signals through a Decoder-Only randomly projected Hypernetwork (D'OH). By directly changing the dimension of a latent code to approximate a target implicit neural architecture, we provide a natural way to vary the memory footprint of neural representations without the costly need for neural architecture search on a space of alternative low-rate structures.

On progressive sharpening, flat minima and generalisation

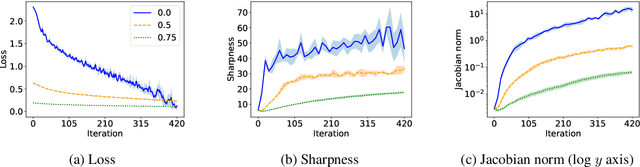
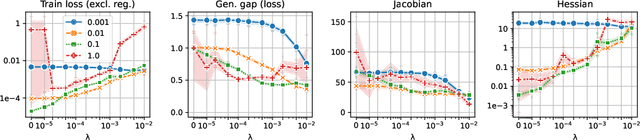
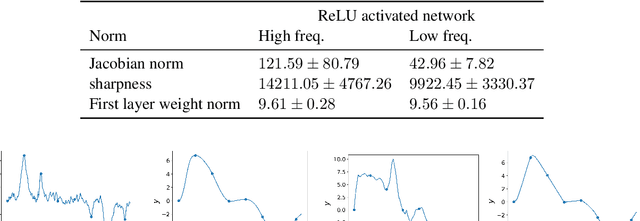
We present a new approach to understanding the relationship between loss curvature and generalisation in deep learning. Specifically, we use existing empirical analyses of the spectrum of deep network loss Hessians to ground an ansatz tying together the loss Hessian and the input-output Jacobian of a deep neural network. We then prove a series of theoretical results which quantify the degree to which the input-output Jacobian of a model approximates its Lipschitz norm over a data distribution, and deduce a novel generalisation bound in terms of the empirical Jacobian. We use our ansatz, together with our theoretical results, to give a new account of the recently observed progressive sharpening phenomenon, as well as the generalisation properties of flat minima. Experimental evidence is provided to validate our claims.

Flow supervision for Deformable NeRF

In this paper we present a new method for deformable NeRF that can directly use optical flow as supervision. We overcome the major challenge with respect to the computationally inefficiency of enforcing the flow constraints to the backward deformation field, used by deformable NeRFs. Specifically, we show that inverting the backward deformation function is actually not needed for computing scene flows between frames. This insight dramatically simplifies the problem, as one is no longer constrained to deformation functions that can be analytically inverted. Instead, thanks to the weak assumptions required by our derivation based on the inverse function theorem, our approach can be extended to a broad class of commonly used backward deformation field. We present results on monocular novel view synthesis with rapid object motion, and demonstrate significant improvements over baselines without flow supervision.

A global analysis of global optimisation

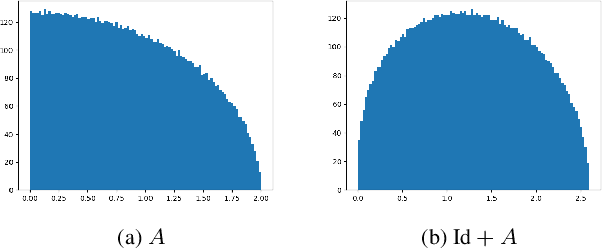
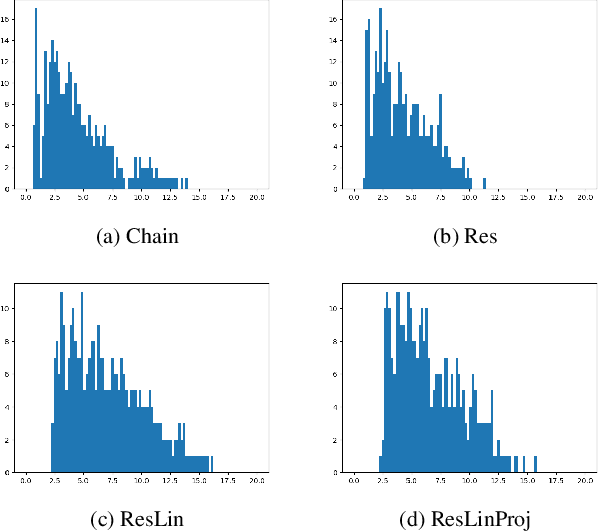
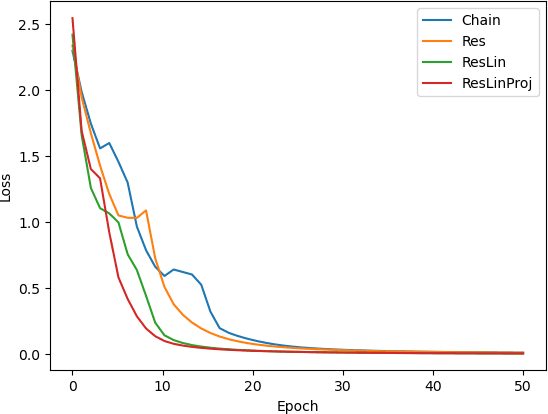
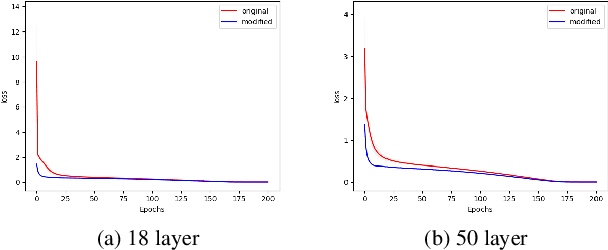
Theoretical understanding of the training of deep neural networks has made great strides in recent years. In particular, it has been shown that sufficient width and sufficiently small learning rate suffice to guarantee that chain networks trained with the square cost converge to global minima close to initialisation. However, this theory cannot apply to the cross-entropy cost, whose global minima exit only at infinity. In this paper, we introduce a general theoretical framework, designed for the study of optimisation, that encompasses ubiquitous architectural choices including batch normalisation, weight normalisation and skip connections. We use our framework to conduct a global analysis of the curvature and regularity properties of neural network loss landscapes, and give two applications. First, we give the first proof that a class of deep neural networks can be trained using gradient descent to global optima even when such optima only exist at infinity. Second, we use the theory in an empirical analysis of the effect of residual connections on training speed, which we verify with ResNets on MNIST, CIFAR10 and CIFAR100.