On progressive sharpening, flat minima and generalisation

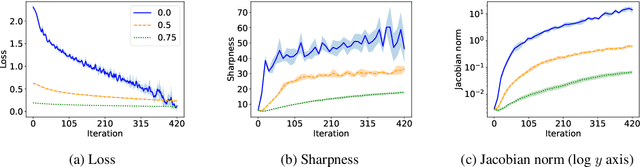
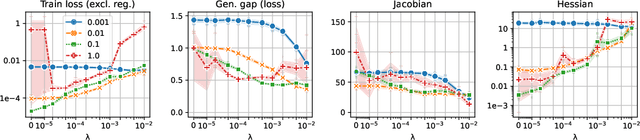
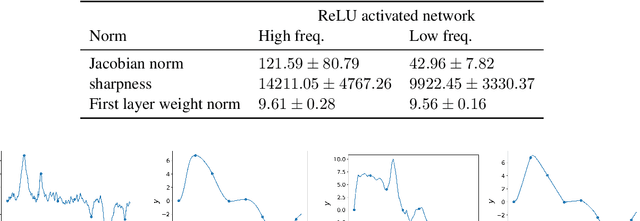
We present a new approach to understanding the relationship between loss curvature and generalisation in deep learning. Specifically, we use existing empirical analyses of the spectrum of deep network loss Hessians to ground an ansatz tying together the loss Hessian and the input-output Jacobian of a deep neural network. We then prove a series of theoretical results which quantify the degree to which the input-output Jacobian of a model approximates its Lipschitz norm over a data distribution, and deduce a novel generalisation bound in terms of the empirical Jacobian. We use our ansatz, together with our theoretical results, to give a new account of the recently observed progressive sharpening phenomenon, as well as the generalisation properties of flat minima. Experimental evidence is provided to validate our claims.