A global analysis of global optimisation

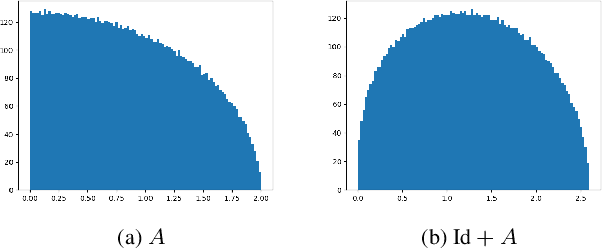
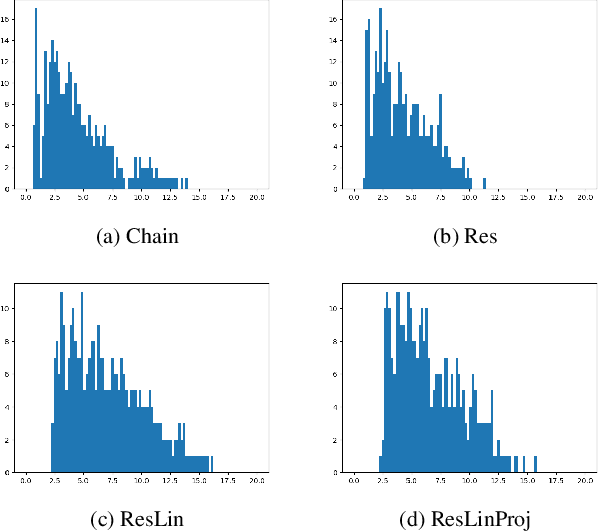
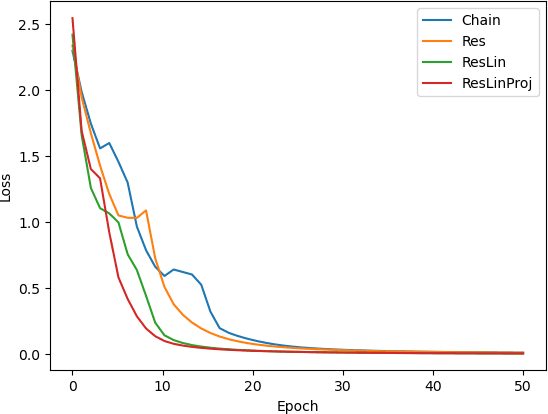
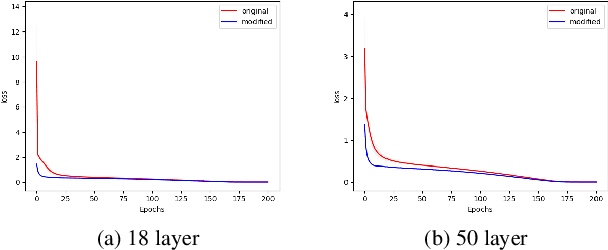
Theoretical understanding of the training of deep neural networks has made great strides in recent years. In particular, it has been shown that sufficient width and sufficiently small learning rate suffice to guarantee that chain networks trained with the square cost converge to global minima close to initialisation. However, this theory cannot apply to the cross-entropy cost, whose global minima exit only at infinity. In this paper, we introduce a general theoretical framework, designed for the study of optimisation, that encompasses ubiquitous architectural choices including batch normalisation, weight normalisation and skip connections. We use our framework to conduct a global analysis of the curvature and regularity properties of neural network loss landscapes, and give two applications. First, we give the first proof that a class of deep neural networks can be trained using gradient descent to global optima even when such optima only exist at infinity. Second, we use the theory in an empirical analysis of the effect of residual connections on training speed, which we verify with ResNets on MNIST, CIFAR10 and CIFAR100.