The Inlet Rank Collapse in Implicit Neural Representations: Diagnosis and Unified Remedy

Implicit Neural Representations (INRs) have revolutionized continuous signal modeling, yet they struggle to recover fine-grained details within finite training budgets. While empirical techniques, such as positional encoding (PE), sinusoidal activations (SIREN), and batch normalization (BN), effectively mitigate this, their theoretical justifications are predominantly post hoc, focusing on the global NTK spectrum only after modifications are applied. In this work, we reverse this paradigm by introducing a structural diagnostic framework. By performing a layer-wise decomposition of the NTK, we mathematically identify the ``Inlet Rank Collapse'': a phenomenon where the low-dimensional input coordinates fail to span the high-dimensional embedding space, creating a fundamental rank deficiency at the first layer that acts as an expressive bottleneck for the entire network. This framework provides a unified perspective to re-interpret PE, SIREN, and BN as different forms of rank restoration. Guided by this diagnosis, we derive a Rank-Expanding Initialization, a minimalist remedy that ensures the representation rank scales with the layer width without architectural modifications or computational overhead. Our results demonstrate that this principled remedy enables standard MLPs to achieve high-fidelity reconstructions, proving that the key to empowering INRs lies in the structural optimization of the initial rank propagation to effectively populate the latent space.

Procedural Pretraining: Warming Up Language Models with Abstract Data

Pretraining directly on web-scale corpora is the de facto paradigm for building language models. We study an alternative setting where the model is initially exposed to abstract structured data, as a means to ease the subsequent acquisition of rich semantic knowledge, much like humans learn simple logic and mathematics before higher reasoning. We specifically focus on procedural data, generated by formal languages and other simple algorithms, as such abstract data. We first diagnose the algorithmic skills that different forms of procedural data can improve, often significantly. For example, on context recall (Needle-in-a-haystack), the accuracy jumps from 10 to 98% when pretraining on Dyck sequences (balanced brackets). Second, we study how these gains are reflected in pretraining larger models (up to 1.3B). We find that front-loading as little as 0.1% procedural data significantly outperforms standard pretraining on natural language, code, and informal mathematics (C4, CodeParrot, and DeepMind-Math datasets). Notably, this procedural pretraining enables the models to reach the same loss value with only 55, 67, 86% of the original data. Third, we explore the mechanisms behind and find that procedural pretraining instils non-trivial structure in both attention and MLP layers. The former is particularly important for structured domains (e.g. code), and the latter for language. Finally, we lay a path for combining multiple forms of procedural data. Our results show that procedural pretraining is a simple, lightweight means to improving performance and accelerating language model pretraining, ultimately suggesting the promise of disentangling knowledge acquisition from reasoning in LLMs.

Can You Learn to See Without Images? Procedural Warm-Up for Vision Transformers

Transformers show remarkable versatility across domains, suggesting the existence of inductive biases beneficial across modalities. In this work, we explore a new way to instil such generic biases in vision transformers (ViTs) by pretraining on procedurally-generated data devoid of visual or semantic content. We generate this data with simple algorithms such as formal grammars, so the results bear no relationship to either natural or synthetic images. We use this procedurally-generated data to pretrain ViTs in a warm-up phase that bypasses their visual patch embedding mechanisms, thus encouraging the models to internalise abstract computational priors. When followed by standard image-based training, this warm-up significantly improves data efficiency, convergence speed, and downstream performance. On ImageNet-1k for example, allocating just 1% of the training budget to procedural data improves final accuracy by over 1.7%. In terms of its effect on performance, 1% procedurally generated data is thus equivalent to 28% of the ImageNet-1k data. These findings suggest a promising path toward new data-efficient and domain-agnostic pretraining strategies.

Data Denoising and Derivative Estimation for Data-Driven Modeling of Nonlinear Dynamical Systems

Data-driven modeling of nonlinear dynamical systems is often hampered by measurement noise. We propose a denoising framework, called Runge-Kutta and Total Variation Based Implicit Neural Representation (RKTV-INR), that represents the state trajectory with an implicit neural representation (INR) fitted directly to noisy observations. Runge-Kutta integration and total variation are imposed as constraints to ensure that the reconstructed state is a trajectory of a dynamical system that remains close to the original data. The trained INR yields a clean, continuous trajectory and provides accurate first-order derivatives via automatic differentiation. These denoised states and derivatives are then supplied to Sparse Identification of Nonlinear Dynamics (SINDy) to recover the governing equations. Experiments demonstrate effective noise suppression, precise derivative estimation, and reliable system identification.

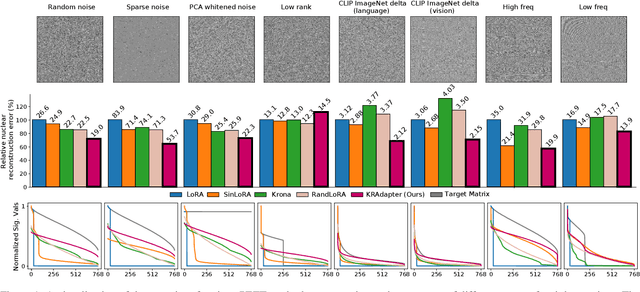
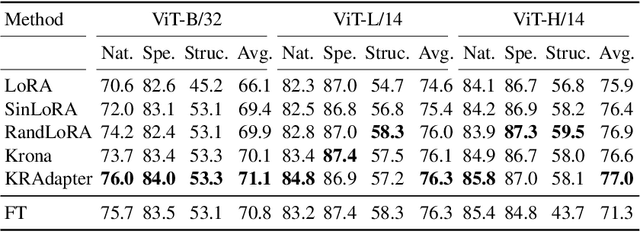
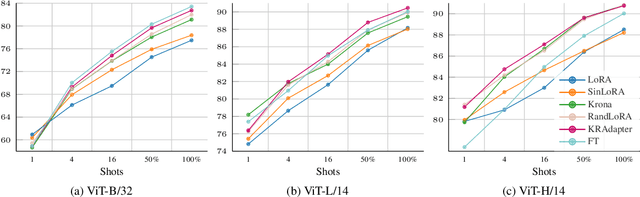
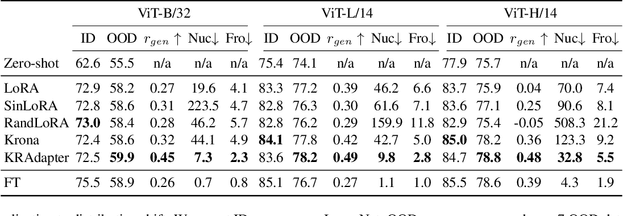
Towards Higher Effective Rank in Parameter-efficient Fine-tuning using Khatri--Rao Product

Parameter-efficient fine-tuning (PEFT) has become a standard approach for adapting large pre-trained models. Amongst PEFT methods, low-rank adaptation (LoRA) has achieved notable success. However, recent studies have highlighted its limitations compared against full-rank alternatives, particularly when applied to multimodal and large language models. In this work, we present a quantitative comparison amongst full-rank and low-rank PEFT methods using a synthetic matrix approximation benchmark with controlled spectral properties. Our results confirm that LoRA struggles to approximate matrices with relatively flat spectrums or high frequency components -- signs of high effective ranks. To this end, we introduce KRAdapter, a novel PEFT algorithm that leverages the Khatri-Rao product to produce weight updates, which, by construction, tends to produce matrix product with a high effective rank. We demonstrate performance gains with KRAdapter on vision-language models up to 1B parameters and on large language models up to 8B parameters, particularly on unseen common-sense reasoning tasks. In addition, KRAdapter maintains the memory and compute efficiency of LoRA, making it a practical and robust alternative to fine-tune billion-scale parameter models.

Compressing Sine-Activated Low-Rank Adapters through Post-Training Quantization

Low-Rank Adaptation (LoRA) has become a standard approach for parameter-efficient fine-tuning, offering substantial reductions in trainable parameters by modeling updates as the product of two low-rank matrices. While effective, the low-rank constraint inherently limits representational capacity, often resulting in reduced performance compared to full-rank fine-tuning. Recent work by Ji et al. (2025) has addressed this limitation by applying a fixed-frequency sinusoidal transformation to low-rank adapters, increasing their stable rank without introducing additional parameters. This raises a crucial question: can the same sine-activated technique be successfully applied within the context of Post-Training Quantization to retain benefits even after model compression? In this paper, we investigate this question by extending the sinusoidal transformation framework to quantized LoRA adapters. We develop a theoretical analysis showing that the stable rank of a quantized adapter is tightly linked to that of its full-precision counterpart, motivating the use of such rank-enhancing functions even under quantization. Our results demonstrate that the expressivity gains from a sinusoidal non-linearity persist after quantization, yielding highly compressed adapters with negligible loss in performance. We validate our approach across a range of fine-tuning tasks for language, vision and text-to-image generation achieving significant memory savings while maintaining competitive accuracy.

Transformers Pretrained on Procedural Data Contain Modular Structures for Algorithmic Reasoning

Pretraining on large, semantically rich datasets is key for developing language models. Surprisingly, recent studies have shown that even synthetic data, generated procedurally through simple semantic-free algorithms, can yield some of the same benefits as natural language pretraining. It is unclear what specific capabilities such simple synthetic data instils in a model, where these capabilities reside in the architecture, and how they manifest within its weights. In this short paper, we identify several beneficial forms of procedural data, together with specific algorithmic reasoning skills that improve in small transformers. Our core finding is that different procedural rules instil distinct but complementary inductive structures in the model. With extensive ablations and partial-transfer experiments, we discover that these structures reside in different parts of the model. Attention layers often carry the most transferable information, but some pretraining rules impart useful structure to MLP blocks instead. Most interestingly, the structures induced by multiple rules can be composed to jointly reinforce multiple capabilities. These results suggest an exciting possibility of disentangling the acquisition of knowledge from reasoning in language models, with the goal of improving their robustness and data efficiency.

Leaner Transformers: More Heads, Less Depth

Transformers have reshaped machine learning by utilizing attention mechanisms to capture complex patterns in large datasets, leading to significant improvements in performance. This success has contributed to the belief that "bigger means better", leading to ever-increasing model sizes. This paper challenge this ideology by showing that many existing transformers might be unnecessarily oversized. We discover a theoretical principle that redefines the role of multi-head attention. An important benefit of the multiple heads is in improving the conditioning of the attention block. We exploit this theoretical insight and redesign popular architectures with an increased number of heads. The improvement in the conditioning proves so significant in practice that model depth can be decreased, reducing the parameter count by up to 30-50% while maintaining accuracy. We obtain consistent benefits across a variety of transformer-based architectures of various scales, on tasks in computer vision (ImageNet-1k) as well as language and sequence modeling (GLUE benchmark, TinyStories, and the Long-Range Arena benchmark).

Structured Initialization for Vision Transformers

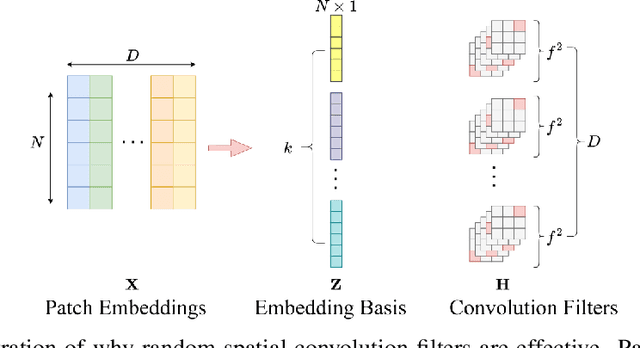
Convolutional Neural Networks (CNNs) inherently encode strong inductive biases, enabling effective generalization on small-scale datasets. In this paper, we propose integrating this inductive bias into ViTs, not through an architectural intervention but solely through initialization. The motivation here is to have a ViT that can enjoy strong CNN-like performance when data assets are small, but can still scale to ViT-like performance as the data expands. Our approach is motivated by our empirical results that random impulse filters can achieve commensurate performance to learned filters within a CNN. We improve upon current ViT initialization strategies, which typically rely on empirical heuristics such as using attention weights from pretrained models or focusing on the distribution of attention weights without enforcing structures. Empirical results demonstrate that our method significantly outperforms standard ViT initialization across numerous small and medium-scale benchmarks, including Food-101, CIFAR-10, CIFAR-100, STL-10, Flowers, and Pets, while maintaining comparative performance on large-scale datasets such as ImageNet-1K. Moreover, our initialization strategy can be easily integrated into various transformer-based architectures such as Swin Transformer and MLP-Mixer with consistent improvements in performance.

Enhancing Transformers Through Conditioned Embedded Tokens

Transformers have transformed modern machine learning, driving breakthroughs in computer vision, natural language processing, and robotics. At the core of their success lies the attention mechanism, which enables the modeling of global dependencies among input tokens. However, we reveal that the attention block in transformers suffers from inherent ill-conditioning, which hampers gradient-based optimization and leads to inefficient training. To address this, we develop a theoretical framework that establishes a direct relationship between the conditioning of the attention block and that of the embedded tokenized data. Building on this insight, we introduce conditioned embedded tokens, a method that systematically modifies the embedded tokens to improve the conditioning of the attention mechanism. Our analysis demonstrates that this approach significantly mitigates ill-conditioning, leading to more stable and efficient training. We validate our methodology across various transformer architectures, achieving consistent improvements in image classification, object detection, instance segmentation, and natural language processing, highlighting its broad applicability and effectiveness.