Invertible Neural Warp for NeRF

This paper tackles the simultaneous optimization of pose and Neural Radiance Fields (NeRF). Departing from the conventional practice of using explicit global representations for camera pose, we propose a novel overparameterized representation that models camera poses as learnable rigid warp functions. We establish that modeling the rigid warps must be tightly coupled with constraints and regularization imposed. Specifically, we highlight the critical importance of enforcing invertibility when learning rigid warp functions via neural network and propose the use of an Invertible Neural Network (INN) coupled with a geometry-informed constraint for this purpose. We present results on synthetic and real-world datasets, and demonstrate that our approach outperforms existing baselines in terms of pose estimation and high-fidelity reconstruction due to enhanced optimization convergence.

Preconditioners for the Stochastic Training of Implicit Neural Representations

Implicit neural representations have emerged as a powerful technique for encoding complex continuous multidimensional signals as neural networks, enabling a wide range of applications in computer vision, robotics, and geometry. While Adam is commonly used for training due to its stochastic proficiency, it entails lengthy training durations. To address this, we explore alternative optimization techniques for accelerated training without sacrificing accuracy. Traditional second-order optimizers like L-BFGS are suboptimal in stochastic settings, making them unsuitable for large-scale data sets. Instead, we propose stochastic training using curvature-aware diagonal preconditioners, showcasing their effectiveness across various signal modalities such as images, shape reconstruction, and Neural Radiance Fields (NeRF).

Analyzing the Neural Tangent Kernel of Periodically Activated Coordinate Networks

Recently, neural networks utilizing periodic activation functions have been proven to demonstrate superior performance in vision tasks compared to traditional ReLU-activated networks. However, there is still a limited understanding of the underlying reasons for this improved performance. In this paper, we aim to address this gap by providing a theoretical understanding of periodically activated networks through an analysis of their Neural Tangent Kernel (NTK). We derive bounds on the minimum eigenvalue of their NTK in the finite width setting, using a fairly general network architecture which requires only one wide layer that grows at least linearly with the number of data samples. Our findings indicate that periodically activated networks are \textit{notably more well-behaved}, from the NTK perspective, than ReLU activated networks. Additionally, we give an application to the memorization capacity of such networks and verify our theoretical predictions empirically. Our study offers a deeper understanding of the properties of periodically activated neural networks and their potential in the field of deep learning.

Architectural Strategies for the optimization of Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) offer a promising avenue for tackling both forward and inverse problems in partial differential equations (PDEs) by incorporating deep learning with fundamental physics principles. Despite their remarkable empirical success, PINNs have garnered a reputation for their notorious training challenges across a spectrum of PDEs. In this work, we delve into the intricacies of PINN optimization from a neural architecture perspective. Leveraging the Neural Tangent Kernel (NTK), our study reveals that Gaussian activations surpass several alternate activations when it comes to effectively training PINNs. Building on insights from numerical linear algebra, we introduce a preconditioned neural architecture, showcasing how such tailored architectures enhance the optimization process. Our theoretical findings are substantiated through rigorous validation against established PDEs within the scientific literature.

Multi-Body Neural Scene Flow

The test-time optimization of scene flow - using a coordinate network as a neural prior - has gained popularity due to its simplicity, lack of dataset bias, and state-of-the-art performance. We observe, however, that although coordinate networks capture general motions by implicitly regularizing the scene flow predictions to be spatially smooth, the neural prior by itself is unable to identify the underlying multi-body rigid motions present in real-world data. To address this, we show that multi-body rigidity can be achieved without the cumbersome and brittle strategy of constraining the $SE(3)$ parameters of each rigid body as done in previous works. This is achieved by regularizing the scene flow optimization to encourage isometry in flow predictions for rigid bodies. This strategy enables multi-body rigidity in scene flow while maintaining a continuous flow field, hence allowing dense long-term scene flow integration across a sequence of point clouds. We conduct extensive experiments on real-world datasets and demonstrate that our approach outperforms the state-of-the-art in 3D scene flow and long-term point-wise 4D trajectory prediction. The code is available at: \href{https://github.com/kavisha725/MBNSF}{https://github.com/kavisha725/MBNSF}.

Curvature-Aware Training for Coordinate Networks

Coordinate networks are widely used in computer vision due to their ability to represent signals as compressed, continuous entities. However, training these networks with first-order optimizers can be slow, hindering their use in real-time applications. Recent works have opted for shallow voxel-based representations to achieve faster training, but this sacrifices memory efficiency. This work proposes a solution that leverages second-order optimization methods to significantly reduce training times for coordinate networks while maintaining their compressibility. Experiments demonstrate the effectiveness of this approach on various signal modalities, such as audio, images, videos, shape reconstruction, and neural radiance fields.

GARF: Gaussian Activated Radiance Fields for High Fidelity Reconstruction and Pose Estimation

Despite Neural Radiance Fields (NeRF) showing compelling results in photorealistic novel views synthesis of real-world scenes, most existing approaches require accurate prior camera poses. Although approaches for jointly recovering the radiance field and camera pose exist (BARF), they rely on a cumbersome coarse-to-fine auxiliary positional embedding to ensure good performance. We present Gaussian Activated neural Radiance Fields (GARF), a new positional embedding-free neural radiance field architecture - employing Gaussian activations - that outperforms the current state-of-the-art in terms of high fidelity reconstruction and pose estimation.

Rotation Coordinate Descent for Fast Globally Optimal Rotation Averaging

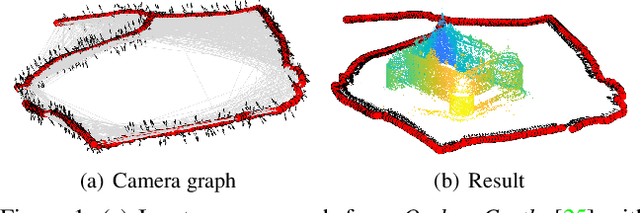
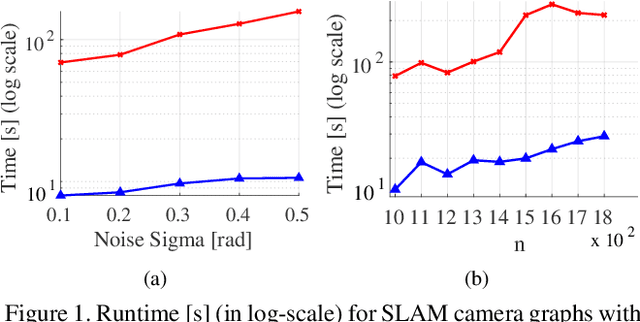
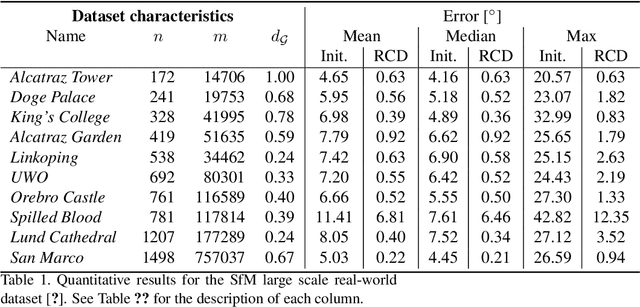
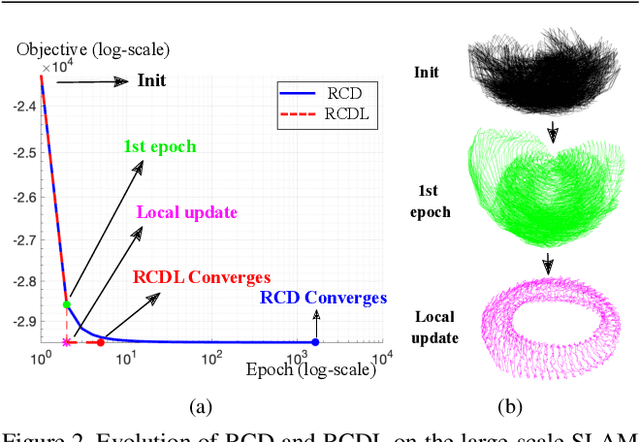
Under mild conditions on the noise level of the measurements, rotation averaging satisfies strong duality, which enables global solutions to be obtained via semidefinite programming (SDP) relaxation. However, generic solvers for SDP are rather slow in practice, even on rotation averaging instances of moderate size, thus developing specialised algorithms is vital. In this paper, we present a fast algorithm that achieves global optimality called rotation coordinate descent (RCD). Unlike block coordinate descent (BCD) which solves SDP by updating the semidefinite matrix in a row-by-row fashion, RCD directly maintains and updates all valid rotations throughout the iterations. This obviates the need to store a large dense semidefinite matrix. We mathematically prove the convergence of our algorithm and empirically show its superior efficiency over state-of-the-art global methods on a variety of problem configurations. Maintaining valid rotations also facilitates incorporating local optimisation routines for further speed-ups. Moreover, our algorithm is simple to implement; see supplementary material for a demonstration program.

Quantum Robust Fitting

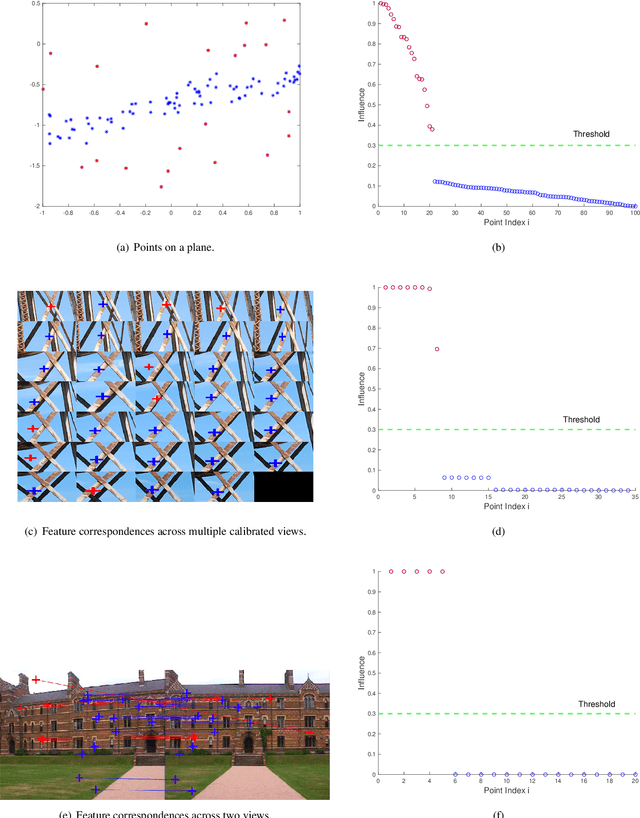
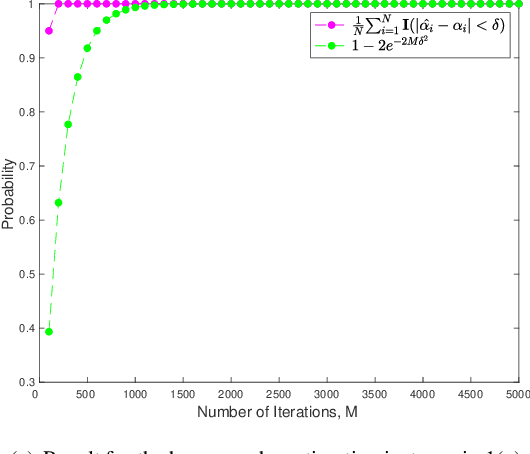
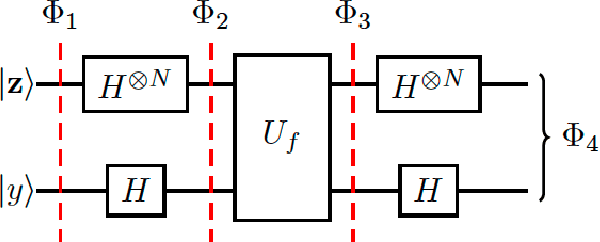
Many computer vision applications need to recover structure from imperfect measurements of the real world. The task is often solved by robustly fitting a geometric model onto noisy and outlier-contaminated data. However, recent theoretical analyses indicate that many commonly used formulations of robust fitting in computer vision are not amenable to tractable solution and approximation. In this paper, we explore the usage of quantum computers for robust fitting. To do so, we examine and establish the practical usefulness of a robust fitting formulation inspired by Fourier analysis of Boolean functions. We then investigate a quantum algorithm to solve the formulation and analyse the computational speed-up possible over the classical algorithm. Our work thus proposes one of the first quantum treatments of robust fitting for computer vision.