Convolutional Filtering with RKHS Algebras

In this paper, we develop a generalized theory of convolutional signal processing and neural networks for Reproducing Kernel Hilbert Spaces (RKHS). Leveraging the theory of algebraic signal processing (ASP), we show that any RKHS allows the formal definition of multiple algebraic convolutional models. We show that any RKHS induces algebras whose elements determine convolutional operators acting on RKHS elements. This approach allows us to achieve scalable filtering and learning as a byproduct of the convolutional model, and simultaneously take advantage of the well-known benefits of processing information in an RKHS. To emphasize the generality and usefulness of our approach, we show how algebraic RKHS can be used to define convolutional signal models on groups, graphons, and traditional Euclidean signal spaces. Furthermore, using algebraic RKHS models, we build convolutional networks, formally defining the notion of pointwise nonlinearities and deriving explicit expressions for the training. Such derivations are obtained in terms of the algebraic representation of the RKHS. We present a set of numerical experiments on real data in which wireless coverage is predicted from measurements captured by unmaned aerial vehicles. This particular real-life scenario emphasizes the benefits of the convolutional RKHS models in neural networks compared to fully connected and standard convolutional operators.

Reinforcement Learning with Almost Sure Constraints

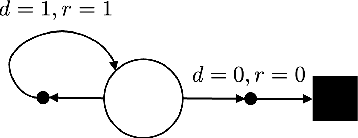
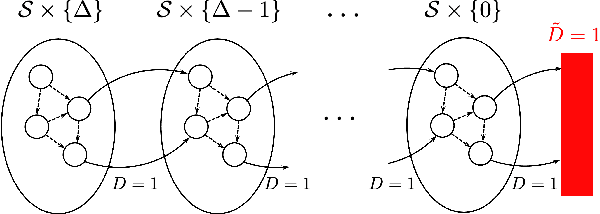
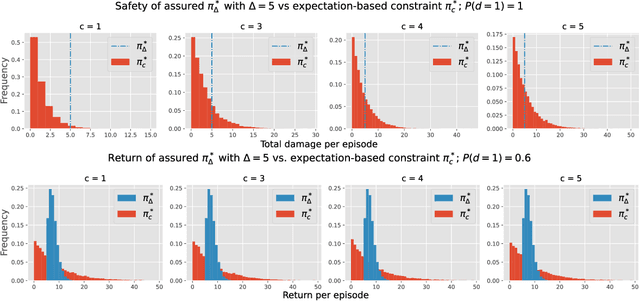
In this work we address the problem of finding feasible policies for Constrained Markov Decision Processes under probability one constraints. We argue that stationary policies are not sufficient for solving this problem, and that a rich class of policies can be found by endowing the controller with a scalar quantity, so called budget, that tracks how close the agent is to violating the constraint. We show that the minimal budget required to act safely can be obtained as the smallest fixed point of a Bellman-like operator, for which we analyze its convergence properties. We also show how to learn this quantity when the true kernel of the Markov decision process is not known, while providing sample-complexity bounds. The utility of knowing this minimal budget relies in that it can aid in the search of optimal or near-optimal policies by shrinking down the region of the state space the agent must navigate. Simulations illustrate the different nature of probability one constraints against the typically used constraints in expectation.

Learning to Act Safely with Limited Exposure and Almost Sure Certainty

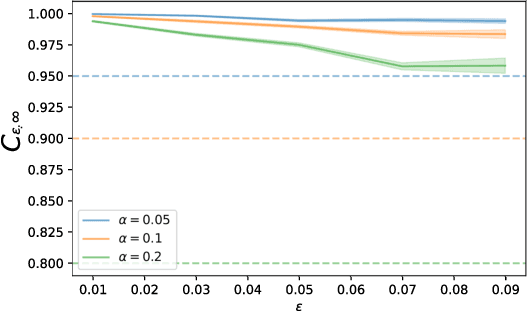
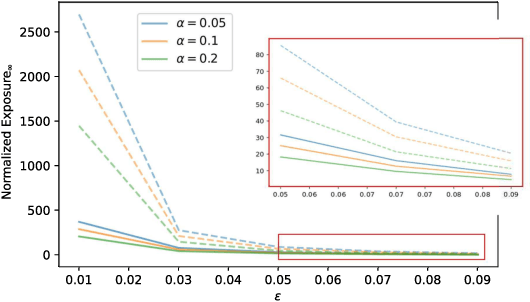
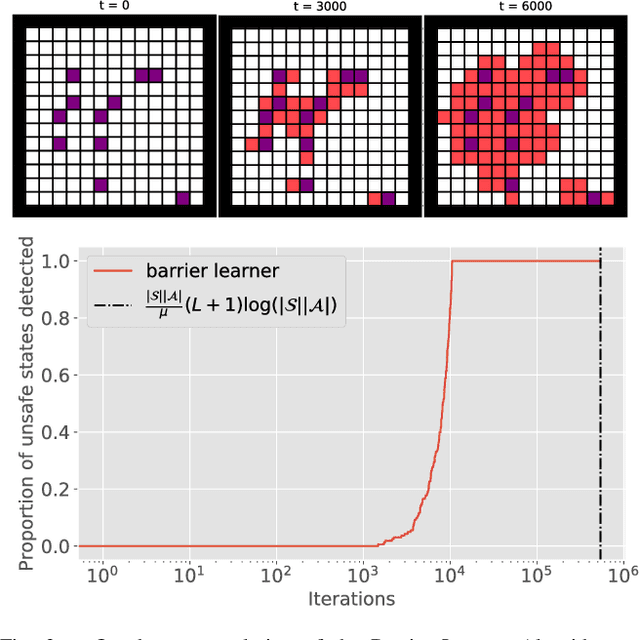
This paper aims to put forward the concept that learning to take safe actions in unknown environments, even with probability one guarantees, can be achieved without the need for an unbounded number of exploratory trials, provided that one is willing to navigate trade-offs between optimality, level of exposure to unsafe events, and the maximum detection time of unsafe actions. We illustrate this concept in two complementary settings. We first focus on the canonical multi-armed bandit problem and seek to study the intrinsic trade-offs of learning safety in the presence of uncertainty. Under mild assumptions on sufficient exploration, we provide an algorithm that provably detects all unsafe machines in an (expected) finite number of rounds. The analysis also unveils a trade-off between the number of rounds needed to secure the environment and the probability of discarding safe machines. We then consider the problem of finding optimal policies for a Markov Decision Process (MDP) with almost sure constraints. We show that the (action) value function satisfies a barrier-based decomposition which allows for the identification of feasible policies independently of the reward process. Using this decomposition, we develop a Barrier-learning algorithm, that identifies such unsafe state-action pairs in a finite expected number of steps. Our analysis further highlights a trade-off between the time lag for the underlying MDP necessary to detect unsafe actions, and the level of exposure to unsafe events. Simulations corroborate our theoretical findings, further illustrating the aforementioned trade-offs, and suggesting that safety constraints can further speed up the learning process.

Assured RL: Reinforcement Learning with Almost Sure Constraints

We consider the problem of finding optimal policies for a Markov Decision Process with almost sure constraints on state transitions and action triplets. We define value and action-value functions that satisfy a barrier-based decomposition which allows for the identification of feasible policies independently of the reward process. We prove that, given a policy {\pi}, certifying whether certain state-action pairs lead to feasible trajectories under {\pi} is equivalent to solving an auxiliary problem aimed at finding the probability of performing an unfeasible transition. Using this interpretation,we develop a Barrier-learning algorithm, based on Q-Learning, that identifies such unsafe state-action pairs. Our analysis motivates the need to enhance the Reinforcement Learning (RL) framework with an additional signal, besides rewards, called here damage function that provides feasibility information and enables the solution of RL problems with model-free constraints. Moreover, our Barrier-learning algorithm wraps around existing RL algorithms, such as Q-Learning and SARSA, giving them the ability to solve almost-surely constrained problems.

Learning to be safe, in finite time

This paper aims to put forward the concept that learning to take safe actions in unknown environments, even with probability one guarantees, can be achieved without the need for an unbounded number of exploratory trials, provided that one is willing to relax its optimality requirements mildly. We focus on the canonical multi-armed bandit problem and seek to study the exploration-preservation trade-off intrinsic within safe learning. More precisely, by defining a handicap metric that counts the number of unsafe actions, we provide an algorithm for discarding unsafe machines (or actions), with probability one, that achieves constant handicap. Our algorithm is rooted in the classical sequential probability ratio test, redefined here for continuing tasks. Under standard assumptions on sufficient exploration, our rule provably detects all unsafe machines in an (expected) finite number of rounds. The analysis also unveils a trade-off between the number of rounds needed to secure the environment and the probability of discarding safe machines. Our decision rule can wrap around any other algorithm to optimize a specific auxiliary goal since it provides a safe environment to search for (approximately) optimal policies. Simulations corroborate our theoretical findings and further illustrate the aforementioned trade-offs.