Bingheng Li
Attention Beyond Neighborhoods: Reviving Transformer for Graph Clustering
Sep 18, 2025Abstract:Attention mechanisms have become a cornerstone in modern neural networks, driving breakthroughs across diverse domains. However, their application to graph structured data, where capturing topological connections is essential, remains underexplored and underperforming compared to Graph Neural Networks (GNNs), particularly in the graph clustering task. GNN tends to overemphasize neighborhood aggregation, leading to a homogenization of node representations. Conversely, Transformer tends to over globalize, highlighting distant nodes at the expense of meaningful local patterns. This dichotomy raises a key question: Is attention inherently redundant for unsupervised graph learning? To address this, we conduct a comprehensive empirical analysis, uncovering the complementary weaknesses of GNN and Transformer in graph clustering. Motivated by these insights, we propose the Attentive Graph Clustering Network (AGCN) a novel architecture that reinterprets the notion that graph is attention. AGCN directly embeds the attention mechanism into the graph structure, enabling effective global information extraction while maintaining sensitivity to local topological cues. Our framework incorporates theoretical analysis to contrast AGCN behavior with GNN and Transformer and introduces two innovations: (1) a KV cache mechanism to improve computational efficiency, and (2) a pairwise margin contrastive loss to boost the discriminative capacity of the attention space. Extensive experimental results demonstrate that AGCN outperforms state-of-the-art methods.
Aggregation-aware MLP: An Unsupervised Approach for Graph Message-passing
Jul 27, 2025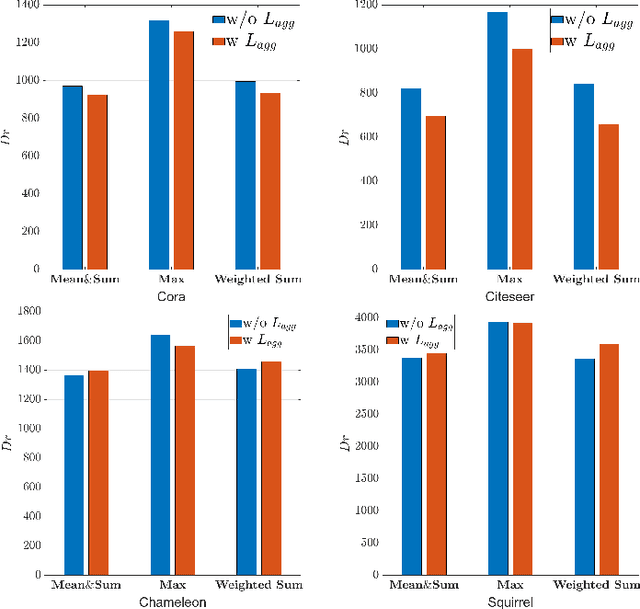

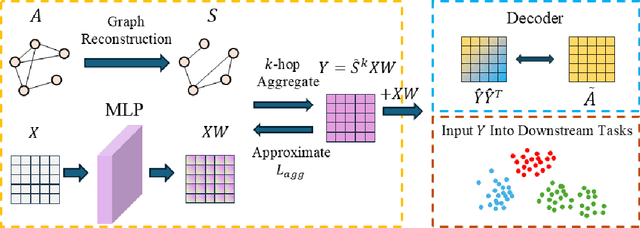
Abstract:Graph Neural Networks (GNNs) have become a dominant approach to learning graph representations, primarily because of their message-passing mechanisms. However, GNNs typically adopt a fixed aggregator function such as Mean, Max, or Sum without principled reasoning behind the selection. This rigidity, especially in the presence of heterophily, often leads to poor, problem dependent performance. Although some attempts address this by designing more sophisticated aggregation functions, these methods tend to rely heavily on labeled data, which is often scarce in real-world tasks. In this work, we propose a novel unsupervised framework, "Aggregation-aware Multilayer Perceptron" (AMLP), which shifts the paradigm from directly crafting aggregation functions to making MLP adaptive to aggregation. Our lightweight approach consists of two key steps: First, we utilize a graph reconstruction method that facilitates high-order grouping effects, and second, we employ a single-layer network to encode varying degrees of heterophily, thereby improving the capacity and applicability of the model. Extensive experiments on node clustering and classification demonstrate the superior performance of AMLP, highlighting its potential for diverse graph learning scenarios.
Homophily Enhanced Graph Domain Adaptation
May 26, 2025



Abstract:Graph Domain Adaptation (GDA) transfers knowledge from labeled source graphs to unlabeled target graphs, addressing the challenge of label scarcity. In this paper, we highlight the significance of graph homophily, a pivotal factor for graph domain alignment, which, however, has long been overlooked in existing approaches. Specifically, our analysis first reveals that homophily discrepancies exist in benchmarks. Moreover, we also show that homophily discrepancies degrade GDA performance from both empirical and theoretical aspects, which further underscores the importance of homophily alignment in GDA. Inspired by this finding, we propose a novel homophily alignment algorithm that employs mixed filters to smooth graph signals, thereby effectively capturing and mitigating homophily discrepancies between graphs. Experimental results on a variety of benchmarks verify the effectiveness of our method.
Higher-order Structure Boosts Link Prediction on Temporal Graphs
May 21, 2025Abstract:Temporal Graph Neural Networks (TGNNs) have gained growing attention for modeling and predicting structures in temporal graphs. However, existing TGNNs primarily focus on pairwise interactions while overlooking higher-order structures that are integral to link formation and evolution in real-world temporal graphs. Meanwhile, these models often suffer from efficiency bottlenecks, further limiting their expressive power. To tackle these challenges, we propose a Higher-order structure Temporal Graph Neural Network, which incorporates hypergraph representations into temporal graph learning. In particular, we develop an algorithm to identify the underlying higher-order structures, enhancing the model's ability to capture the group interactions. Furthermore, by aggregating multiple edge features into hyperedge representations, HTGN effectively reduces memory cost during training. We theoretically demonstrate the enhanced expressiveness of our approach and validate its effectiveness and efficiency through extensive experiments on various real-world temporal graphs. Experimental results show that HTGN achieves superior performance on dynamic link prediction while reducing memory costs by up to 50\% compared to existing methods.
Unveiling Mode Connectivity in Graph Neural Networks
Feb 18, 2025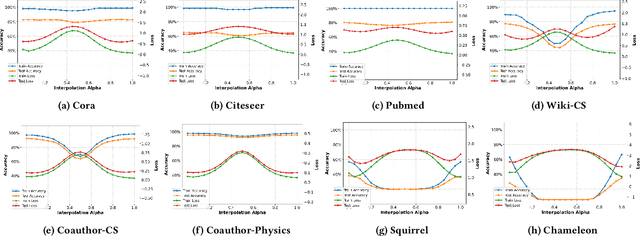
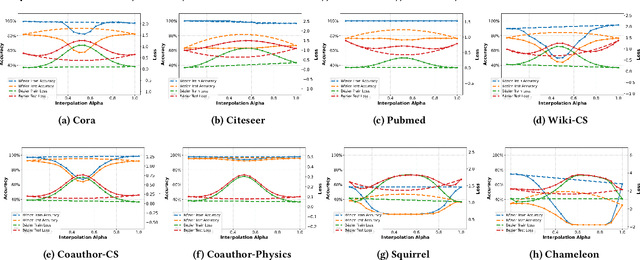
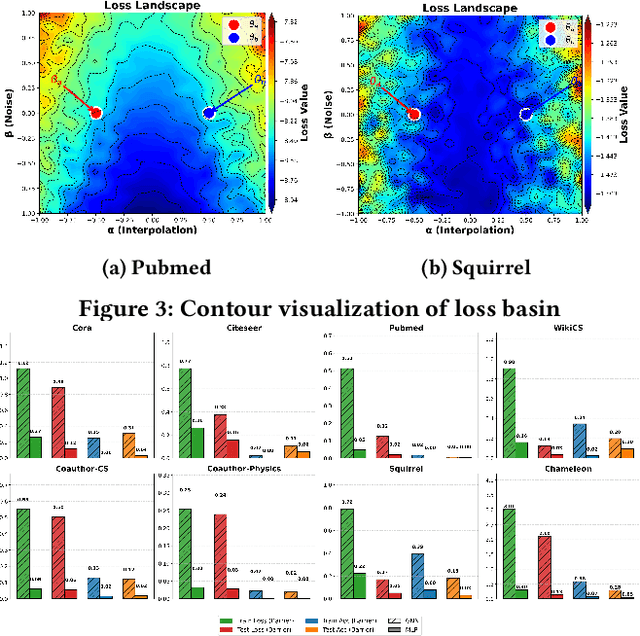
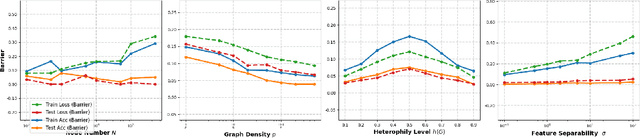
Abstract:A fundamental challenge in understanding graph neural networks (GNNs) lies in characterizing their optimization dynamics and loss landscape geometry, critical for improving interpretability and robustness. While mode connectivity, a lens for analyzing geometric properties of loss landscapes has proven insightful for other deep learning architectures, its implications for GNNs remain unexplored. This work presents the first investigation of mode connectivity in GNNs. We uncover that GNNs exhibit distinct non-linear mode connectivity, diverging from patterns observed in fully-connected networks or CNNs. Crucially, we demonstrate that graph structure, rather than model architecture, dominates this behavior, with graph properties like homophily correlating with mode connectivity patterns. We further establish a link between mode connectivity and generalization, proposing a generalization bound based on loss barriers and revealing its utility as a diagnostic tool. Our findings further bridge theoretical insights with practical implications: they rationalize domain alignment strategies in graph learning and provide a foundation for refining GNN training paradigms.
One Node One Model: Featuring the Missing-Half for Graph Clustering
Dec 13, 2024



Abstract:Most existing graph clustering methods primarily focus on exploiting topological structure, often neglecting the ``missing-half" node feature information, especially how these features can enhance clustering performance. This issue is further compounded by the challenges associated with high-dimensional features. Feature selection in graph clustering is particularly difficult because it requires simultaneously discovering clusters and identifying the relevant features for these clusters. To address this gap, we introduce a novel paradigm called ``one node one model", which builds an exclusive model for each node and defines the node label as a combination of predictions for node groups. Specifically, the proposed ``Feature Personalized Graph Clustering (FPGC)" method identifies cluster-relevant features for each node using a squeeze-and-excitation block, integrating these features into each model to form the final representations. Additionally, the concept of feature cross is developed as a data augmentation technique to learn low-order feature interactions. Extensive experimental results demonstrate that FPGC outperforms state-of-the-art clustering methods. Moreover, the plug-and-play nature of our method provides a versatile solution to enhance GNN-based models from a feature perspective.
An Efficient Unsupervised Framework for Convex Quadratic Programs via Deep Unrolling
Dec 02, 2024



Abstract:Quadratic programs (QPs) arise in various domains such as machine learning, finance, and control. Recently, learning-enhanced primal-dual hybrid gradient (PDHG) methods have shown great potential in addressing large-scale linear programs; however, this approach has not been extended to QPs. In this work, we focus on unrolling "PDQP", a PDHG algorithm specialized for convex QPs. Specifically, we propose a neural network model called "PDQP-net" to learn optimal QP solutions. Theoretically, we demonstrate that a PDQP-net of polynomial size can align with the PDQP algorithm, returning optimal primal-dual solution pairs. We propose an unsupervised method that incorporates KKT conditions into the loss function. Unlike the standard learning-to-optimize framework that requires optimization solutions generated by solvers, our unsupervised method adjusts the network weights directly from the evaluation of the primal-dual gap. This method has two benefits over supervised learning: first, it helps generate better primal-dual gap since the primal-dual gap is in the objective function; second, it does not require solvers. We show that PDQP-net trained in this unsupervised manner can effectively approximate optimal QP solutions. Extensive numerical experiments confirm our findings, indicating that using PDQP-net predictions to warm-start PDQP can achieve up to 45% acceleration on QP instances. Moreover, it achieves 14% to 31% acceleration on out-of-distribution instances.
Towards Knowledge Checking in Retrieval-augmented Generation: A Representation Perspective
Nov 21, 2024Abstract:Retrieval-Augmented Generation (RAG) systems have shown promise in enhancing the performance of Large Language Models (LLMs). However, these systems face challenges in effectively integrating external knowledge with the LLM's internal knowledge, often leading to issues with misleading or unhelpful information. This work aims to provide a systematic study on knowledge checking in RAG systems. We conduct a comprehensive analysis of LLM representation behaviors and demonstrate the significance of using representations in knowledge checking. Motivated by the findings, we further develop representation-based classifiers for knowledge filtering. We show substantial improvements in RAG performance, even when dealing with noisy knowledge databases. Our study provides new insights into leveraging LLM representations for enhancing the reliability and effectiveness of RAG systems.
Text-space Graph Foundation Models: Comprehensive Benchmarks and New Insights
Jun 15, 2024



Abstract:Given the ubiquity of graph data and its applications in diverse domains, building a Graph Foundation Model (GFM) that can work well across different graphs and tasks with a unified backbone has recently garnered significant interests. A major obstacle to achieving this goal stems from the fact that graphs from different domains often exhibit diverse node features. Inspired by multi-modal models that align different modalities with natural language, the text has recently been adopted to provide a unified feature space for diverse graphs. Despite the great potential of these text-space GFMs, current research in this field is hampered by two problems. First, the absence of a comprehensive benchmark with unified problem settings hinders a clear understanding of the comparative effectiveness and practical value of different text-space GFMs. Second, there is a lack of sufficient datasets to thoroughly explore the methods' full potential and verify their effectiveness across diverse settings. To address these issues, we conduct a comprehensive benchmark providing novel text-space datasets and comprehensive evaluation under unified problem settings. Empirical results provide new insights and inspire future research directions. Our code and data are publicly available from \url{https://github.com/CurryTang/TSGFM}.
PDHG-Unrolled Learning-to-Optimize Method for Large-Scale Linear Programming
Jun 04, 2024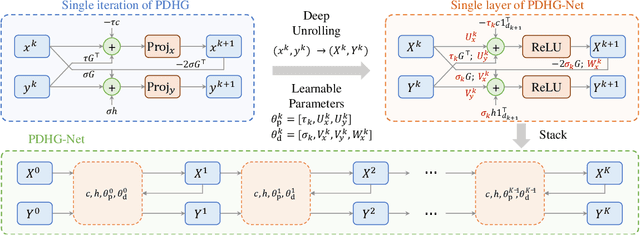
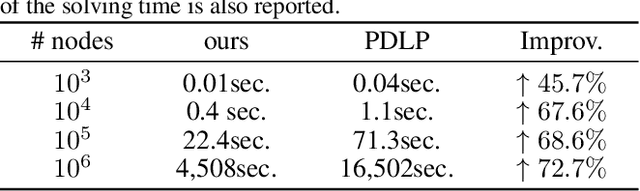
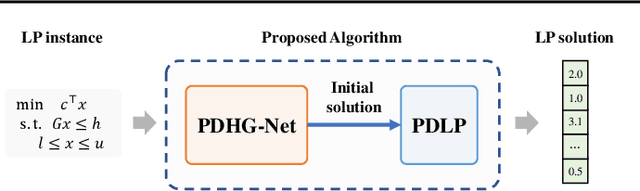
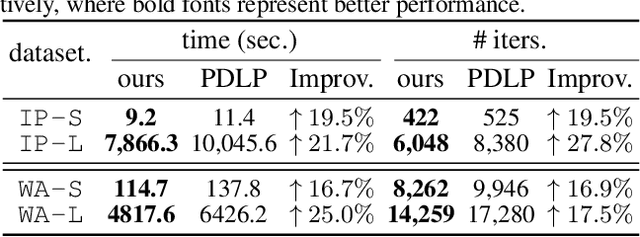
Abstract:Solving large-scale linear programming (LP) problems is an important task in various areas such as communication networks, power systems, finance and logistics. Recently, two distinct approaches have emerged to expedite LP solving: (i) First-order methods (FOMs); (ii) Learning to optimize (L2O). In this work, we propose an FOM-unrolled neural network (NN) called PDHG-Net, and propose a two-stage L2O method to solve large-scale LP problems. The new architecture PDHG-Net is designed by unrolling the recently emerged PDHG method into a neural network, combined with channel-expansion techniques borrowed from graph neural networks. We prove that the proposed PDHG-Net can recover PDHG algorithm, thus can approximate optimal solutions of LP instances with a polynomial number of neurons. We propose a two-stage inference approach: first use PDHG-Net to generate an approximate solution, and then apply PDHG algorithm to further improve the solution. Experiments show that our approach can significantly accelerate LP solving, achieving up to a 3$\times$ speedup compared to FOMs for large-scale LP problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge