MoFO: Momentum-Filtered Optimizer for Mitigating Forgetting in LLM Fine-Tuning

Recently, large language models (LLMs) have demonstrated remarkable capabilities in a wide range of tasks. Typically, an LLM is pre-trained on large corpora and subsequently fine-tuned on task-specific datasets. However, during fine-tuning, LLMs may forget the knowledge acquired in the pre-training stage, leading to a decline in general capabilities. To address this issue, we propose a new fine-tuning algorithm termed Momentum-Filtered Optimizer (MoFO). The key idea of MoFO is to iteratively select and update the model parameters with the largest momentum magnitudes. Compared to full-parameter training, MoFO achieves similar fine-tuning performance while keeping parameters closer to the pre-trained model, thereby mitigating knowledge forgetting. Unlike most existing methods for forgetting mitigation, MoFO combines the following two advantages. First, MoFO does not require access to pre-training data. This makes MoFO particularly suitable for fine-tuning scenarios where pre-training data is unavailable, such as fine-tuning checkpoint-only open-source LLMs. Second, MoFO does not alter the original loss function. This could avoid impairing the model performance on the fine-tuning tasks. We validate MoFO through rigorous convergence analysis and extensive experiments, demonstrating its superiority over existing methods in mitigating forgetting and enhancing fine-tuning performance.

PDHG-Unrolled Learning-to-Optimize Method for Large-Scale Linear Programming

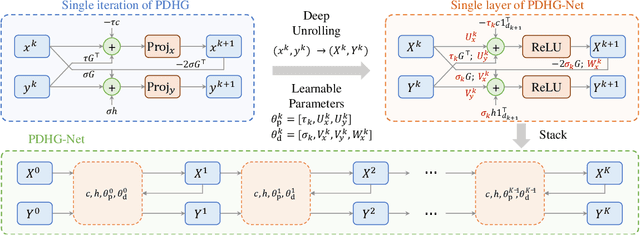
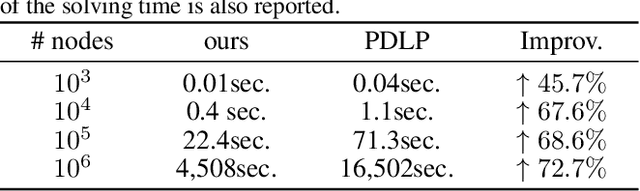
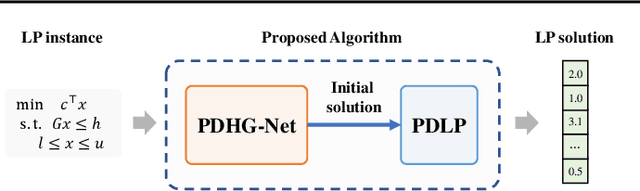
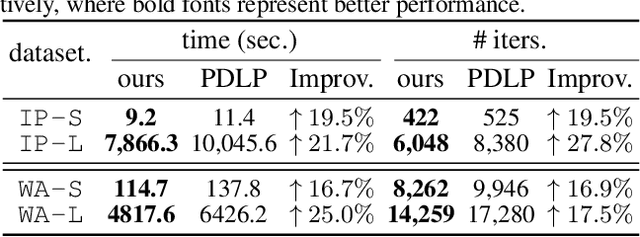
Solving large-scale linear programming (LP) problems is an important task in various areas such as communication networks, power systems, finance and logistics. Recently, two distinct approaches have emerged to expedite LP solving: (i) First-order methods (FOMs); (ii) Learning to optimize (L2O). In this work, we propose an FOM-unrolled neural network (NN) called PDHG-Net, and propose a two-stage L2O method to solve large-scale LP problems. The new architecture PDHG-Net is designed by unrolling the recently emerged PDHG method into a neural network, combined with channel-expansion techniques borrowed from graph neural networks. We prove that the proposed PDHG-Net can recover PDHG algorithm, thus can approximate optimal solutions of LP instances with a polynomial number of neurons. We propose a two-stage inference approach: first use PDHG-Net to generate an approximate solution, and then apply PDHG algorithm to further improve the solution. Experiments show that our approach can significantly accelerate LP solving, achieving up to a 3$\times$ speedup compared to FOMs for large-scale LP problems.