ORGEval: Graph-Theoretic Evaluation of LLMs in Optimization Modeling

Formulating optimization problems for industrial applications demands significant manual effort and domain expertise. While Large Language Models (LLMs) show promise in automating this process, evaluating their performance remains difficult due to the absence of robust metrics. Existing solver-based approaches often face inconsistency, infeasibility issues, and high computational costs. To address these issues, we propose ORGEval, a graph-theoretic evaluation framework for assessing LLMs' capabilities in formulating linear and mixed-integer linear programs. ORGEval represents optimization models as graphs, reducing equivalence detection to graph isomorphism testing. We identify and prove a sufficient condition, when the tested graphs are symmetric decomposable (SD), under which the Weisfeiler-Lehman (WL) test is guaranteed to correctly detect isomorphism. Building on this, ORGEval integrates a tailored variant of the WL-test with an SD detection algorithm to evaluate model equivalence. By focusing on structural equivalence rather than instance-level configurations, ORGEval is robust to numerical variations. Experimental results show that our method can successfully detect model equivalence and produce 100\% consistent results across random parameter configurations, while significantly outperforming solver-based methods in runtime, especially on difficult problems. Leveraging ORGEval, we construct the Bench4Opt dataset and benchmark state-of-the-art LLMs on optimization modeling. Our results reveal that although optimization modeling remains challenging for all LLMs, DeepSeek-V3 and Claude-Opus-4 achieve the highest accuracies under direct prompting, outperforming even leading reasoning models.

Bridging Formal Language with Chain-of-Thought Reasoning to Geometry Problem Solving

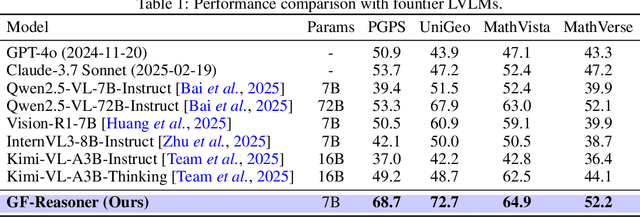
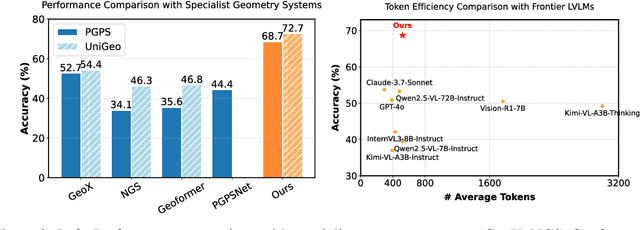
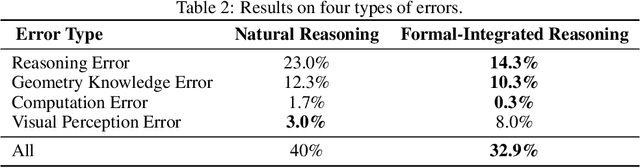
Large vision language models exhibit notable limitations on Geometry Problem Solving (GPS) because of their unreliable diagram interpretation and pure natural-language reasoning. A recent line of work mitigates this by using symbolic solvers: the model directly generates a formal program that a geometry solver can execute. However, this direct program generation lacks intermediate reasoning, making the decision process opaque and prone to errors. In this work, we explore a new approach that integrates Chain-of-Thought (CoT) with formal language. The model interleaves natural language reasoning with incremental emission of solver-executable code, producing a hybrid reasoning trace in which critical derivations are expressed in formal language. To teach this behavior at scale, we combine (1) supervised fine-tuning on an 11K newly developed synthetic dataset with interleaved natural language reasoning and automatic formalization, and (2) solver-in-the-loop reinforcement learning that jointly optimizes both the CoT narrative and the resulting program through outcome-based rewards. Built on Qwen2.5-VL-7B, our new model, named GF-Reasoner, achieves up to 15% accuracy improvements on standard GPS benchmarks, surpassing both 7B-scale peers and the much larger model Qwen2.5-VL-72B. By exploiting high-order geometric knowledge and offloading symbolic computation to the solver, the generated reasoning traces are noticeably shorter and cleaner. Furthermore, we present a comprehensive analysis of method design choices (e.g., reasoning paradigms, data synthesis, training epochs, etc.), providing actionable insights for future research.

CoRT: Code-integrated Reasoning within Thinking

Large Reasoning Models (LRMs) like o1 and DeepSeek-R1 have shown remarkable progress in natural language reasoning with long chain-of-thought (CoT), yet they remain inefficient or inaccurate when handling complex mathematical operations. Addressing these limitations through computational tools (e.g., computation libraries and symbolic solvers) is promising, but it introduces a technical challenge: Code Interpreter (CI) brings external knowledge beyond the model's internal text representations, thus the direct combination is not efficient. This paper introduces CoRT, a post-training framework for teaching LRMs to leverage CI effectively and efficiently. As a first step, we address the data scarcity issue by synthesizing code-integrated reasoning data through Hint-Engineering, which strategically inserts different hints at appropriate positions to optimize LRM-CI interaction. We manually create 30 high-quality samples, upon which we post-train models ranging from 1.5B to 32B parameters, with supervised fine-tuning, rejection fine-tuning and reinforcement learning. Our experimental results demonstrate that Hint-Engineering models achieve 4\% and 8\% absolute improvements on DeepSeek-R1-Distill-Qwen-32B and DeepSeek-R1-Distill-Qwen-1.5B respectively, across five challenging mathematical reasoning datasets. Furthermore, Hint-Engineering models use about 30\% fewer tokens for the 32B model and 50\% fewer tokens for the 1.5B model compared with the natural language models. The models and code are available at https://github.com/ChengpengLi1003/CoRT.

RealCritic: Towards Effectiveness-Driven Evaluation of Language Model Critiques

Critiques are important for enhancing the performance of Large Language Models (LLMs), enabling both self-improvement and constructive feedback for others by identifying flaws and suggesting improvements. However, evaluating the critique capabilities of LLMs presents a significant challenge due to the open-ended nature of the task. In this work, we introduce a new benchmark designed to assess the critique capabilities of LLMs. Unlike existing benchmarks, which typically function in an open-loop fashion, our approach employs a closed-loop methodology that evaluates the quality of corrections generated from critiques. Moreover, the benchmark incorporates features such as self-critique, cross-critique, and iterative critique, which are crucial for distinguishing the abilities of advanced reasoning models from more classical ones. We implement this benchmark using eight challenging reasoning tasks. We have several interesting findings. First, despite demonstrating comparable performance in direct chain-of-thought generation, classical LLMs significantly lag behind the advanced reasoning-based model o1-mini across all critique scenarios. Second, in self-critique and iterative critique settings, classical LLMs may even underperform relative to their baseline capabilities. We hope that this benchmark will serve as a valuable resource to guide future advancements. The code and data are available at \url{https://github.com/tangzhy/RealCritic}.

Enabling Scalable Oversight via Self-Evolving Critic

Despite their remarkable performance, the development of Large Language Models (LLMs) faces a critical challenge in scalable oversight: providing effective feedback for tasks where human evaluation is difficult or where LLMs outperform humans. While there is growing interest in using LLMs for critique, current approaches still rely on human annotations or more powerful models, leaving the issue of enhancing critique capabilities without external supervision unresolved. We introduce SCRIT (Self-evolving CRITic), a framework that enables genuine self-evolution of critique abilities. Technically, SCRIT self-improves by training on synthetic data, generated by a contrastive-based self-critic that uses reference solutions for step-by-step critique, and a self-validation mechanism that ensures critique quality through correction outcomes. Implemented with Qwen2.5-72B-Instruct, one of the most powerful LLMs, SCRIT achieves up to a 10.3\% improvement on critique-correction and error identification benchmarks. Our analysis reveals that SCRIT's performance scales positively with data and model size, outperforms alternative approaches, and benefits critically from its self-validation component.

An Efficient Unsupervised Framework for Convex Quadratic Programs via Deep Unrolling

Quadratic programs (QPs) arise in various domains such as machine learning, finance, and control. Recently, learning-enhanced primal-dual hybrid gradient (PDHG) methods have shown great potential in addressing large-scale linear programs; however, this approach has not been extended to QPs. In this work, we focus on unrolling "PDQP", a PDHG algorithm specialized for convex QPs. Specifically, we propose a neural network model called "PDQP-net" to learn optimal QP solutions. Theoretically, we demonstrate that a PDQP-net of polynomial size can align with the PDQP algorithm, returning optimal primal-dual solution pairs. We propose an unsupervised method that incorporates KKT conditions into the loss function. Unlike the standard learning-to-optimize framework that requires optimization solutions generated by solvers, our unsupervised method adjusts the network weights directly from the evaluation of the primal-dual gap. This method has two benefits over supervised learning: first, it helps generate better primal-dual gap since the primal-dual gap is in the objective function; second, it does not require solvers. We show that PDQP-net trained in this unsupervised manner can effectively approximate optimal QP solutions. Extensive numerical experiments confirm our findings, indicating that using PDQP-net predictions to warm-start PDQP can achieve up to 45% acceleration on QP instances. Moreover, it achieves 14% to 31% acceleration on out-of-distribution instances.

MoFO: Momentum-Filtered Optimizer for Mitigating Forgetting in LLM Fine-Tuning

Recently, large language models (LLMs) have demonstrated remarkable capabilities in a wide range of tasks. Typically, an LLM is pre-trained on large corpora and subsequently fine-tuned on task-specific datasets. However, during fine-tuning, LLMs may forget the knowledge acquired in the pre-training stage, leading to a decline in general capabilities. To address this issue, we propose a new fine-tuning algorithm termed Momentum-Filtered Optimizer (MoFO). The key idea of MoFO is to iteratively select and update the model parameters with the largest momentum magnitudes. Compared to full-parameter training, MoFO achieves similar fine-tuning performance while keeping parameters closer to the pre-trained model, thereby mitigating knowledge forgetting. Unlike most existing methods for forgetting mitigation, MoFO combines the following two advantages. First, MoFO does not require access to pre-training data. This makes MoFO particularly suitable for fine-tuning scenarios where pre-training data is unavailable, such as fine-tuning checkpoint-only open-source LLMs. Second, MoFO does not alter the original loss function. This could avoid impairing the model performance on the fine-tuning tasks. We validate MoFO through rigorous convergence analysis and extensive experiments, demonstrating its superiority over existing methods in mitigating forgetting and enhancing fine-tuning performance.

Adam-mini: Use Fewer Learning Rates To Gain More

We propose Adam-mini, an optimizer that achieves on-par or better performance than AdamW with 45% to 50% less memory footprint. Adam-mini reduces memory by cutting down the learning rate resources in Adam (i.e., $1/\sqrt{v}$). We find that $\geq$ 90% of these learning rates in $v$ could be harmlessly removed if we (1) carefully partition the parameters into blocks following our proposed principle on Hessian structure; (2) assign a single but good learning rate to each parameter block. We further find that, for each of these parameter blocks, there exists a single high-quality learning rate that can outperform Adam, provided that sufficient resources are available to search it out. We then provide one cost-effective way to find good learning rates and propose Adam-mini. Empirically, we verify that Adam-mini performs on par or better than AdamW on various language models sized from 125M to 7B for pre-training, supervised fine-tuning, and RLHF. The reduced memory footprint of Adam-mini also alleviates communication overheads among GPUs and CPUs, thereby increasing throughput. For instance, Adam-mini achieves 49.6% higher throughput than AdamW when pre-training Llama2-7B on $2\times$ A800-80GB GPUs, which saves 33% wall-clock time for pre-training.

PDHG-Unrolled Learning-to-Optimize Method for Large-Scale Linear Programming

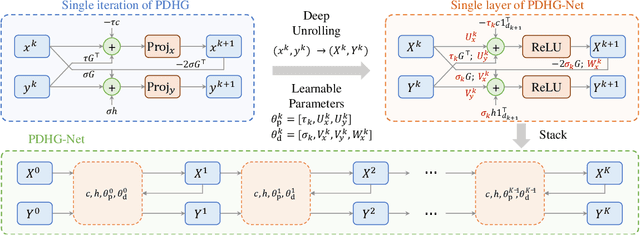
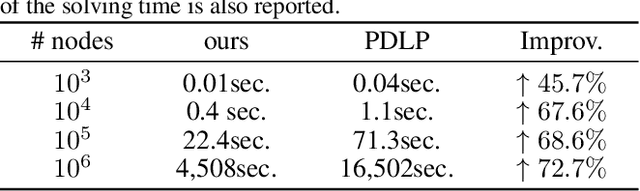
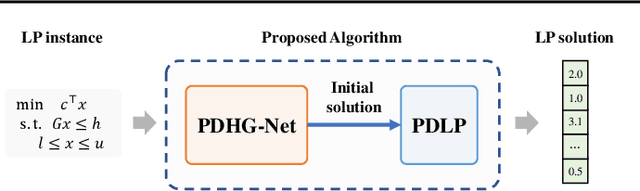
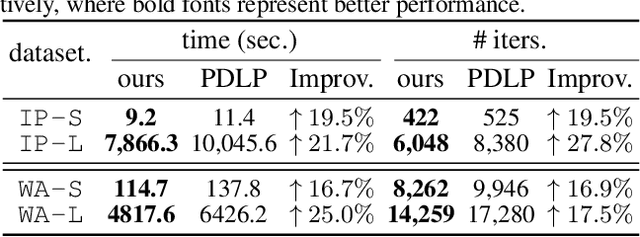
Solving large-scale linear programming (LP) problems is an important task in various areas such as communication networks, power systems, finance and logistics. Recently, two distinct approaches have emerged to expedite LP solving: (i) First-order methods (FOMs); (ii) Learning to optimize (L2O). In this work, we propose an FOM-unrolled neural network (NN) called PDHG-Net, and propose a two-stage L2O method to solve large-scale LP problems. The new architecture PDHG-Net is designed by unrolling the recently emerged PDHG method into a neural network, combined with channel-expansion techniques borrowed from graph neural networks. We prove that the proposed PDHG-Net can recover PDHG algorithm, thus can approximate optimal solutions of LP instances with a polynomial number of neurons. We propose a two-stage inference approach: first use PDHG-Net to generate an approximate solution, and then apply PDHG algorithm to further improve the solution. Experiments show that our approach can significantly accelerate LP solving, achieving up to a 3$\times$ speedup compared to FOMs for large-scale LP problems.

Why Transformers Need Adam: A Hessian Perspective

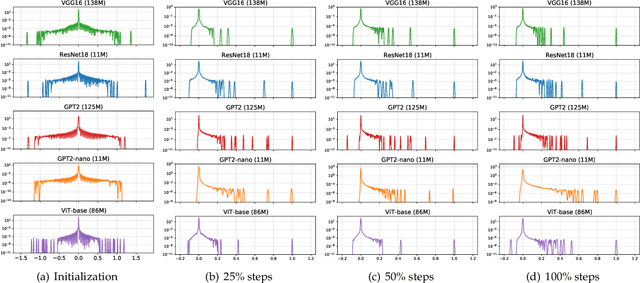
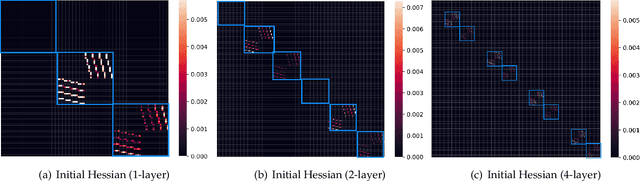
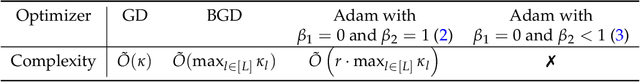
SGD performs worse than Adam by a significant margin on Transformers, but the reason remains unclear. In this work, we provide an explanation of SGD's failure on Transformers through the lens of Hessian: (i) Transformers are ``heterogeneous'': the Hessian spectrum across parameter blocks vary dramatically, a phenomenon we call ``block heterogeneity"; (ii) Heterogeneity hampers SGD: SGD performs badly on problems with block heterogeneity. To validate that heterogeneity hampers SGD, we check various Transformers, CNNs, MLPs, and quadratic problems, and find that SGD works well on problems without block heterogeneity but performs badly when the heterogeneity exists. Our initial theoretical analysis indicates that SGD fails because it applies one single learning rate for all blocks, which cannot handle the heterogeneity among blocks. The failure could be rescued if we could assign different learning rates across blocks, as designed in Adam.