Qwen2.5-Math Technical Report: Toward Mathematical Expert Model via Self-Improvement

In this report, we present a series of math-specific large language models: Qwen2.5-Math and Qwen2.5-Math-Instruct-1.5B/7B/72B. The core innovation of the Qwen2.5 series lies in integrating the philosophy of self-improvement throughout the entire pipeline, from pre-training and post-training to inference: (1) During the pre-training phase, Qwen2-Math-Instruct is utilized to generate large-scale, high-quality mathematical data. (2) In the post-training phase, we develop a reward model (RM) by conducting massive sampling from Qwen2-Math-Instruct. This RM is then applied to the iterative evolution of data in supervised fine-tuning (SFT). With a stronger SFT model, it's possible to iteratively train and update the RM, which in turn guides the next round of SFT data iteration. On the final SFT model, we employ the ultimate RM for reinforcement learning, resulting in the Qwen2.5-Math-Instruct. (3) Furthermore, during the inference stage, the RM is used to guide sampling, optimizing the model's performance. Qwen2.5-Math-Instruct supports both Chinese and English, and possess advanced mathematical reasoning capabilities, including Chain-of-Thought (CoT) and Tool-Integrated Reasoning (TIR). We evaluate our models on 10 mathematics datasets in both English and Chinese, such as GSM8K, MATH, GaoKao, AMC23, and AIME24, covering a range of difficulties from grade school level to math competition problems.

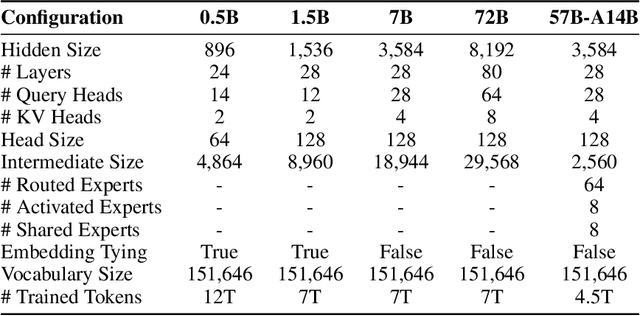
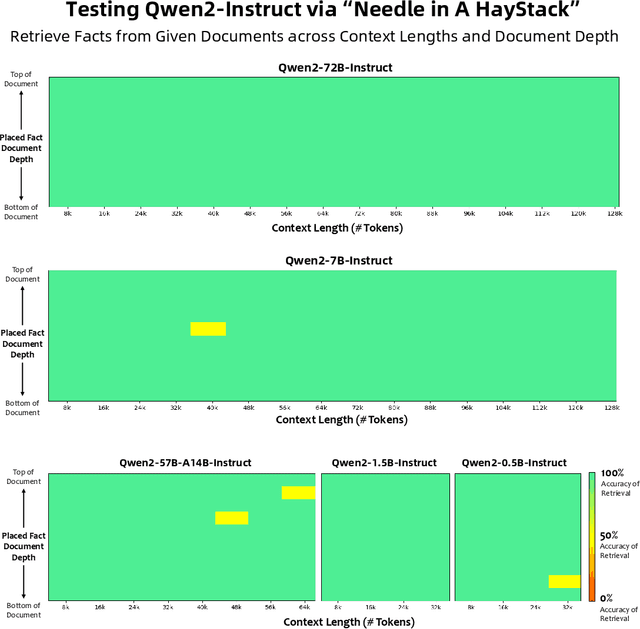
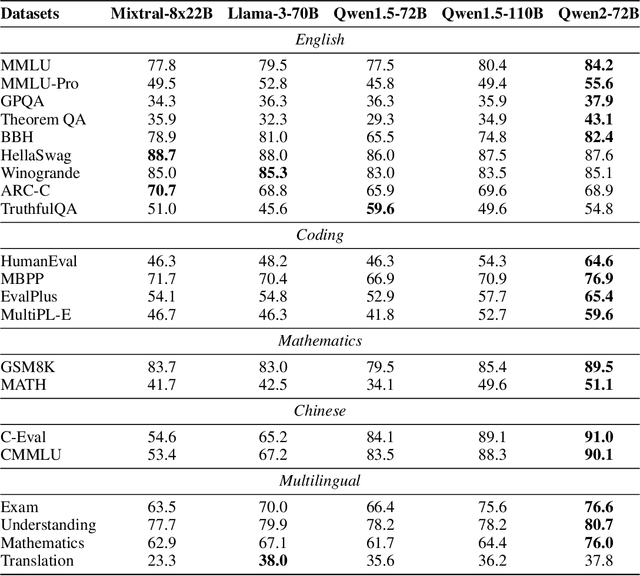
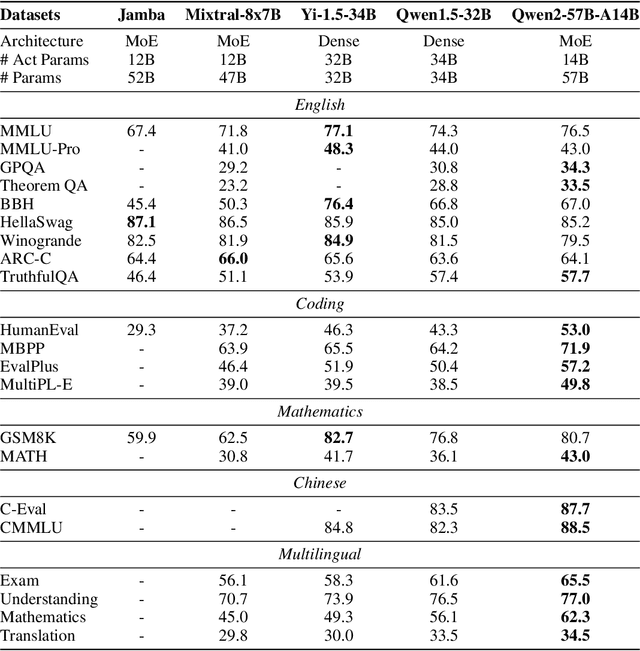
Qwen2 Technical Report

This report introduces the Qwen2 series, the latest addition to our large language models and large multimodal models. We release a comprehensive suite of foundational and instruction-tuned language models, encompassing a parameter range from 0.5 to 72 billion, featuring dense models and a Mixture-of-Experts model. Qwen2 surpasses most prior open-weight models, including its predecessor Qwen1.5, and exhibits competitive performance relative to proprietary models across diverse benchmarks on language understanding, generation, multilingual proficiency, coding, mathematics, and reasoning. The flagship model, Qwen2-72B, showcases remarkable performance: 84.2 on MMLU, 37.9 on GPQA, 64.6 on HumanEval, 89.5 on GSM8K, and 82.4 on BBH as a base language model. The instruction-tuned variant, Qwen2-72B-Instruct, attains 9.1 on MT-Bench, 48.1 on Arena-Hard, and 35.7 on LiveCodeBench. Moreover, Qwen2 demonstrates robust multilingual capabilities, proficient in approximately 30 languages, spanning English, Chinese, Spanish, French, German, Arabic, Russian, Korean, Japanese, Thai, Vietnamese, and more, underscoring its versatility and global reach. To foster community innovation and accessibility, we have made the Qwen2 model weights openly available on Hugging Face and ModelScope, and the supplementary materials including example code on GitHub. These platforms also include resources for quantization, fine-tuning, and deployment, facilitating a wide range of applications and research endeavors.

DotaMath: Decomposition of Thought with Code Assistance and Self-correction for Mathematical Reasoning

Large language models (LLMs) have made impressive progress in handling simple math problems, yet they still struggle with more challenging and complex mathematical tasks. In this paper, we introduce a series of LLMs that employs the Decomposition of thought with code assistance and self-correction for mathematical reasoning, dubbed as DotaMath. DotaMath models tackle complex mathematical tasks by decomposing them into simpler logical subtasks, leveraging code to solve these subtasks, obtaining fine-grained feedback from the code interpreter, and engaging in self-reflection and correction. By annotating diverse interactive tool-use trajectories and employing query evolution on GSM8K and MATH datasets, we generate an instruction fine-tuning dataset called DotaMathQA with 574K query-response pairs. We train a series of base LLMs using imitation learning on DotaMathQA, resulting in DotaMath models that achieve remarkable performance compared to open-source LLMs across various in-domain and out-of-domain benchmarks. Notably, DotaMath-deepseek-7B showcases an outstanding performance of 64.8% on the competitive MATH dataset and 86.7% on GSM8K. Besides, DotaMath-deepseek-7B maintains strong competitiveness on a series of in-domain and out-of-domain benchmarks (Avg. 80.1%). Looking forward, we anticipate that the DotaMath paradigm will open new pathways for addressing intricate mathematical problems. Our code is publicly available at https://github.com/ChengpengLi1003/DotaMath.

Self-play with Execution Feedback: Improving Instruction-following Capabilities of Large Language Models

One core capability of large language models (LLMs) is to follow natural language instructions. However, the issue of automatically constructing high-quality training data to enhance the complex instruction-following abilities of LLMs without manual annotation remains unresolved. In this paper, we introduce AutoIF, the first scalable and reliable method for automatically generating instruction-following training data. AutoIF transforms the validation of instruction-following data quality into code verification, requiring LLMs to generate instructions, the corresponding code to check the correctness of the instruction responses, and unit test samples to verify the code's correctness. Then, execution feedback-based rejection sampling can generate data for Supervised Fine-Tuning (SFT) and Reinforcement Learning from Human Feedback (RLHF) training. AutoIF achieves significant improvements across three training algorithms, SFT, Offline DPO, and Online DPO, when applied to the top open-source LLMs, Qwen2 and LLaMA3, in self-alignment and strong-to-weak distillation settings. Our code is publicly available at https://github.com/QwenLM/AutoIF.

Model-enhanced Contrastive Reinforcement Learning for Sequential Recommendation

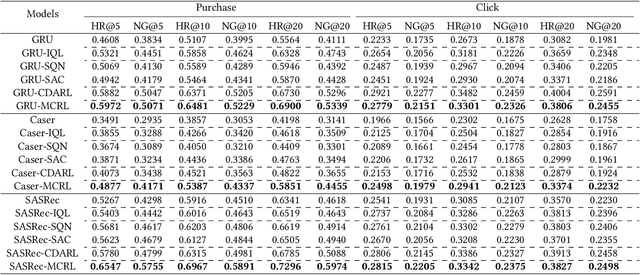
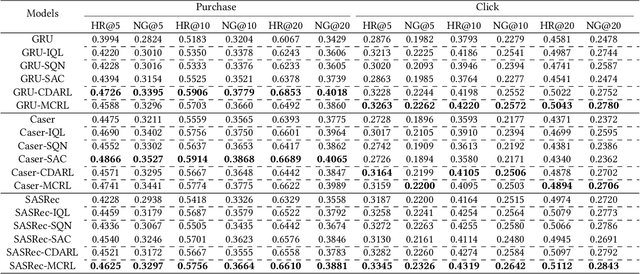
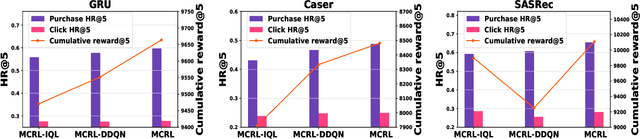
Reinforcement learning (RL) has been widely applied in recommendation systems due to its potential in optimizing the long-term engagement of users. From the perspective of RL, recommendation can be formulated as a Markov decision process (MDP), where recommendation system (agent) can interact with users (environment) and acquire feedback (reward signals).However, it is impractical to conduct online interactions with the concern on user experience and implementation complexity, and we can only train RL recommenders with offline datasets containing limited reward signals and state transitions. Therefore, the data sparsity issue of reward signals and state transitions is very severe, while it has long been overlooked by existing RL recommenders.Worse still, RL methods learn through the trial-and-error mode, but negative feedback cannot be obtained in implicit feedback recommendation tasks, which aggravates the overestimation problem of offline RL recommender. To address these challenges, we propose a novel RL recommender named model-enhanced contrastive reinforcement learning (MCRL). On the one hand, we learn a value function to estimate the long-term engagement of users, together with a conservative value learning mechanism to alleviate the overestimation problem.On the other hand, we construct some positive and negative state-action pairs to model the reward function and state transition function with contrastive learning to exploit the internal structure information of MDP. Experiments demonstrate that the proposed method significantly outperforms existing offline RL and self-supervised RL methods with different representative backbone networks on two real-world datasets.

Query and Response Augmentation Cannot Help Out-of-domain Math Reasoning Generalization

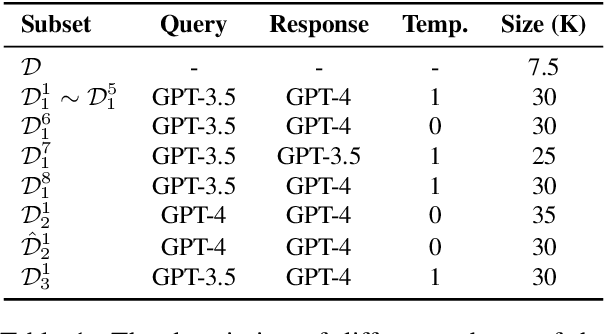
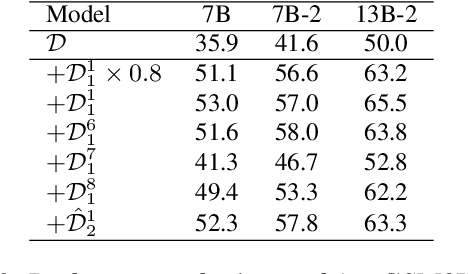
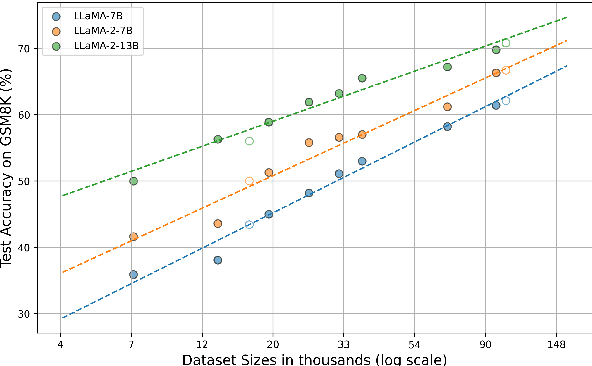
In math reasoning with large language models (LLMs), fine-tuning data augmentation by query evolution and diverse reasoning paths is empirically verified effective, profoundly narrowing the gap between open-sourced LLMs and cutting-edge proprietary LLMs. In this paper, we conduct an investigation for such data augmentation in math reasoning and are intended to answer: (1) What strategies of data augmentation are more effective; (2) What is the scaling relationship between the amount of augmented data and model performance; and (3) Can data augmentation incentivize generalization to out-of-domain mathematical reasoning tasks? To this end, we create a new dataset, AugGSM8K, by complicating and diversifying the queries from GSM8K and sampling multiple reasoning paths. We obtained a series of LLMs called MuggleMath by fine-tuning on subsets of AugGSM8K. MuggleMath substantially achieves new state-of-the-art on GSM8K (from 54% to 68.4% at the scale of 7B, and from 63.9% to 74.0% at the scale of 13B). A log-linear relationship is presented between MuggleMath's performance and the amount of augmented data. We also find that MuggleMath is weak in out-of-domain math reasoning generalization to MATH. This is attributed to the differences in query distribution between AugGSM8K and MATH which suggest that augmentation on a single benchmark could not help with overall math reasoning performance. Codes and AugGSM8K will be uploaded to https://github.com/OFA-Sys/gsm8k-ScRel.

How Abilities in Large Language Models are Affected by Supervised Fine-tuning Data Composition

Large language models (LLMs) with enormous pre-training tokens and parameter amounts emerge abilities, including math reasoning, code generation, and instruction following. These abilities are further enhanced by supervised fine-tuning (SFT). The open-source community has studied on ad-hoc SFT for each ability, while proprietary LLMs are versatile for all abilities. It is important to investigate how to unlock them with multiple abilities via SFT. In this study, we specifically focus on the data composition between mathematical reasoning, code generation, and general human-aligning abilities during SFT. From a scaling perspective, we investigate the relationship between model abilities and various factors including data amounts, data composition ratio, model parameters, and SFT strategies. Our experiments reveal that different abilities exhibit different scaling patterns, and larger models generally show superior performance with the same amount of data. Mathematical reasoning and code generation improve as data amounts increase consistently, while the general ability is enhanced with about a thousand samples and improves slowly. We find data composition results in various abilities improvements with low data amounts, while conflicts of abilities with high data amounts. Our experiments further show that composition data amount impacts performance, while the influence of composition ratio is insignificant. Regarding the SFT strategies, we evaluate sequential learning multiple abilities are prone to catastrophic forgetting. Our proposed Dual-stage Mixed Fine-tuning (DMT) strategy learns specialized abilities first and then learns general abilities with a small amount of specialized data to prevent forgetting, offering a promising solution to learn multiple abilities with different scaling patterns.

Scaling Relationship on Learning Mathematical Reasoning with Large Language Models

Mathematical reasoning is a challenging task for large language models (LLMs), while the scaling relationship of it with respect to LLM capacity is under-explored. In this paper, we investigate how the pre-training loss, supervised data amount, and augmented data amount influence the reasoning performances of a supervised LLM. We find that pre-training loss is a better indicator of the model's performance than the model's parameter count. We apply supervised fine-tuning (SFT) with different amounts of supervised data and empirically find a log-linear relation between data amount and model performance, and we find better models improve less with enlarged supervised datasets. To augment more data samples for improving model performances without any human effort, we propose to apply Rejection sampling Fine-Tuning (RFT). RFT uses supervised models to generate and collect correct reasoning paths as augmented fine-tuning datasets. We find with augmented samples containing more distinct reasoning paths, RFT improves mathematical reasoning performance more for LLMs. We also find RFT brings more improvement for less performant LLMs. Furthermore, we combine rejection samples from multiple models which push LLaMA-7B to an accuracy of 49.3% and outperforms the supervised fine-tuning (SFT) accuracy of 35.9% significantly.