AngleRoCL: Angle-Robust Concept Learning for Physically View-Invariant T2I Adversarial Patches

Cutting-edge works have demonstrated that text-to-image (T2I) diffusion models can generate adversarial patches that mislead state-of-the-art object detectors in the physical world, revealing detectors' vulnerabilities and risks. However, these methods neglect the T2I patches' attack effectiveness when observed from different views in the physical world (i.e., angle robustness of the T2I adversarial patches). In this paper, we study the angle robustness of T2I adversarial patches comprehensively, revealing their angle-robust issues, demonstrating that texts affect the angle robustness of generated patches significantly, and task-specific linguistic instructions fail to enhance the angle robustness. Motivated by the studies, we introduce Angle-Robust Concept Learning (AngleRoCL), a simple and flexible approach that learns a generalizable concept (i.e., text embeddings in implementation) representing the capability of generating angle-robust patches. The learned concept can be incorporated into textual prompts and guides T2I models to generate patches with their attack effectiveness inherently resistant to viewpoint variations. Through extensive simulation and physical-world experiments on five SOTA detectors across multiple views, we demonstrate that AngleRoCL significantly enhances the angle robustness of T2I adversarial patches compared to baseline methods. Our patches maintain high attack success rates even under challenging viewing conditions, with over 50% average relative improvement in attack effectiveness across multiple angles. This research advances the understanding of physically angle-robust patches and provides insights into the relationship between textual concepts and physical properties in T2I-generated contents.

Model Enumeration of Two-Variable Logic with Quadratic Delay Complexity

We study the model enumeration problem of the function-free, finite domain fragment of first-order logic with two variables ($FO^2$). Specifically, given an $FO^2$ sentence $\Gamma$ and a positive integer $n$, how can one enumerate all the models of $\Gamma$ over a domain of size $n$? In this paper, we devise a novel algorithm to address this problem. The delay complexity, the time required between producing two consecutive models, of our algorithm is quadratic in the given domain size $n$ (up to logarithmic factors) when the sentence is fixed. This complexity is almost optimal since the interpretation of binary predicates in any model requires at least $\Omega(n^2)$ bits to represent.

Visibility-Uncertainty-guided 3D Gaussian Inpainting via Scene Conceptional Learning

3D Gaussian Splatting (3DGS) has emerged as a powerful and efficient 3D representation for novel view synthesis. This paper extends 3DGS capabilities to inpainting, where masked objects in a scene are replaced with new contents that blend seamlessly with the surroundings. Unlike 2D image inpainting, 3D Gaussian inpainting (3DGI) is challenging in effectively leveraging complementary visual and semantic cues from multiple input views, as occluded areas in one view may be visible in others. To address this, we propose a method that measures the visibility uncertainties of 3D points across different input views and uses them to guide 3DGI in utilizing complementary visual cues. We also employ uncertainties to learn a semantic concept of scene without the masked object and use a diffusion model to fill masked objects in input images based on the learned concept. Finally, we build a novel 3DGI framework, VISTA, by integrating VISibility-uncerTainty-guided 3DGI with scene conceptuAl learning. VISTA generates high-quality 3DGS models capable of synthesizing artifact-free and naturally inpainted novel views. Furthermore, our approach extends to handling dynamic distractors arising from temporal object changes, enhancing its versatility in diverse scene reconstruction scenarios. We demonstrate the superior performance of our method over state-of-the-art techniques using two challenging datasets: the SPIn-NeRF dataset, featuring 10 diverse static 3D inpainting scenes, and an underwater 3D inpainting dataset derived from UTB180, including fast-moving fish as inpainting targets.

An Efficient Unsupervised Framework for Convex Quadratic Programs via Deep Unrolling

Quadratic programs (QPs) arise in various domains such as machine learning, finance, and control. Recently, learning-enhanced primal-dual hybrid gradient (PDHG) methods have shown great potential in addressing large-scale linear programs; however, this approach has not been extended to QPs. In this work, we focus on unrolling "PDQP", a PDHG algorithm specialized for convex QPs. Specifically, we propose a neural network model called "PDQP-net" to learn optimal QP solutions. Theoretically, we demonstrate that a PDQP-net of polynomial size can align with the PDQP algorithm, returning optimal primal-dual solution pairs. We propose an unsupervised method that incorporates KKT conditions into the loss function. Unlike the standard learning-to-optimize framework that requires optimization solutions generated by solvers, our unsupervised method adjusts the network weights directly from the evaluation of the primal-dual gap. This method has two benefits over supervised learning: first, it helps generate better primal-dual gap since the primal-dual gap is in the objective function; second, it does not require solvers. We show that PDQP-net trained in this unsupervised manner can effectively approximate optimal QP solutions. Extensive numerical experiments confirm our findings, indicating that using PDQP-net predictions to warm-start PDQP can achieve up to 45% acceleration on QP instances. Moreover, it achieves 14% to 31% acceleration on out-of-distribution instances.

Bridging Weighted First Order Model Counting and Graph Polynomials

The Weighted First-Order Model Counting Problem (WFOMC) asks to compute the weighted sum of models of a given first-order logic sentence over a given domain. It can be solved in time polynomial in the domain size for sentences from the two-variable fragment with counting quantifiers, known as $C^2$. This polynomial-time complexity is also retained when extending $C^2$ by one of the following axioms: linear order axiom, tree axiom, forest axiom, directed acyclic graph axiom or connectedness axiom. An interesting question remains as to which other axioms can be added to the first-order sentences in this way. We provide a new perspective on this problem by associating WFOMC with graph polynomials. Using WFOMC, we define Weak Connectedness Polynomial and Strong Connectedness Polynomials for first-order logic sentences. It turns out that these polynomials have the following interesting properties. First, they can be computed in polynomial time in the domain size for sentences from $C^2$. Second, we can use them to solve WFOMC with all of the existing axioms known to be tractable as well as with new ones such as bipartiteness, strong connectedness, being a spanning subgraph, having $k$ connected components, etc. Third, the well-known Tutte polynomial can be recovered as a special case of the Weak Connectedness Polynomial, and the Strict and Non-Strict Directed Chromatic Polynomials can be recovered from the Strong Connectedness Polynomials, which allows us to show that these important graph polynomials can be computed in time polynomial in the number of vertices for any graph that can be encoded by a fixed $C^2$ sentence and a conjunction of an arbitrary number of ground unary literals.

Music Style Transfer With Diffusion Model

Previous studies on music style transfer have mainly focused on one-to-one style conversion, which is relatively limited. When considering the conversion between multiple styles, previous methods required designing multiple modes to disentangle the complex style of the music, resulting in large computational costs and slow audio generation. The existing music style transfer methods generate spectrograms with artifacts, leading to significant noise in the generated audio. To address these issues, this study proposes a music style transfer framework based on diffusion models (DM) and uses spectrogram-based methods to achieve multi-to-multi music style transfer. The GuideDiff method is used to restore spectrograms to high-fidelity audio, accelerating audio generation speed and reducing noise in the generated audio. Experimental results show that our model has good performance in multi-mode music style transfer compared to the baseline and can generate high-quality audio in real-time on consumer-grade GPUs.

Lifted Algorithms for Symmetric Weighted First-Order Model Sampling

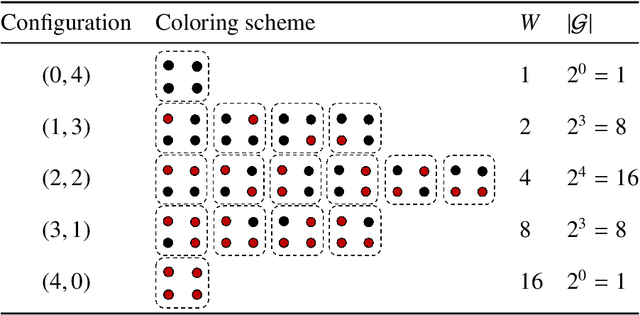
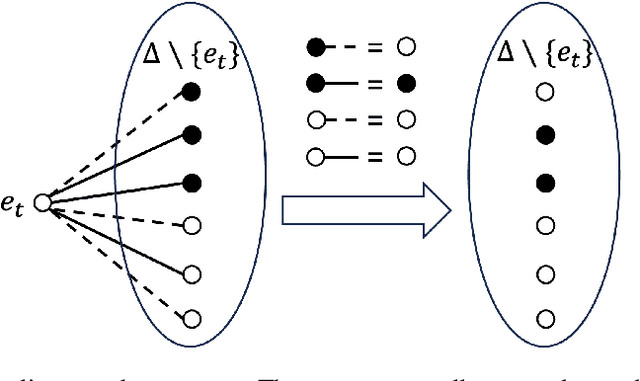
Weighted model counting (WMC) is the task of computing the weighted sum of all satisfying assignments (i.e., models) of a propositional formula. Similarly, weighted model sampling (WMS) aims to randomly generate models with probability proportional to their respective weights. Both WMC and WMS are hard to solve exactly, falling under the $\#\mathsf{P}$-hard complexity class. However, it is known that the counting problem may sometimes be tractable, if the propositional formula can be compactly represented and expressed in first-order logic. In such cases, model counting problems can be solved in time polynomial in the domain size, and are known as domain-liftable. The following question then arises: Is it also the case for weighted model sampling? This paper addresses this question and answers it affirmatively. Specifically, we prove the domain-liftability under sampling for the two-variables fragment of first-order logic with counting quantifiers in this paper, by devising an efficient sampling algorithm for this fragment that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of cardinality constraints. To empirically verify our approach, we conduct experiments over various first-order formulas designed for the uniform generation of combinatorial structures and sampling in statistical-relational models. The results demonstrate that our algorithm outperforms a start-of-the-art WMS sampler by a substantial margin, confirming the theoretical results.

AGTGAN: Unpaired Image Translation for Photographic Ancient Character Generation

The study of ancient writings has great value for archaeology and philology. Essential forms of material are photographic characters, but manual photographic character recognition is extremely time-consuming and expertise-dependent. Automatic classification is therefore greatly desired. However, the current performance is limited due to the lack of annotated data. Data generation is an inexpensive but useful solution for data scarcity. Nevertheless, the diverse glyph shapes and complex background textures of photographic ancient characters make the generation task difficult, leading to the unsatisfactory results of existing methods. In this paper, we propose an unsupervised generative adversarial network called AGTGAN. By the explicit global and local glyph shape style modeling followed by the stroke-aware texture transfer, as well as an associate adversarial learning mechanism, our method can generate characters with diverse glyphs and realistic textures. We evaluate our approach on the photographic ancient character datasets, e.g., OBC306 and CSDD. Our method outperforms the state-of-the-art approaches in various metrics and performs much better in terms of the diversity and authenticity of generated samples. With our generated images, experiments on the largest photographic oracle bone character dataset show that our method can achieve a significant increase in classification accuracy, up to 16.34%.

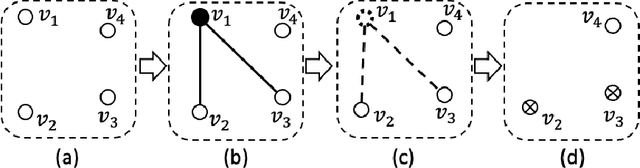
On Exact Sampling in the Two-Variable Fragment of First-Order Logic

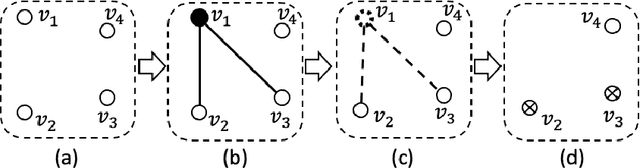
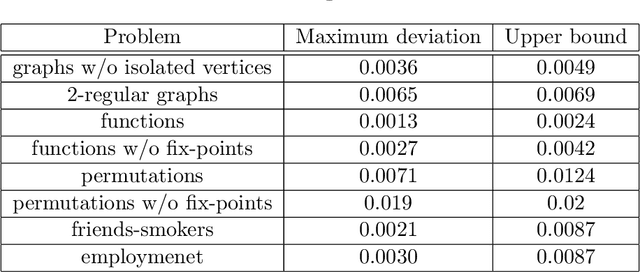
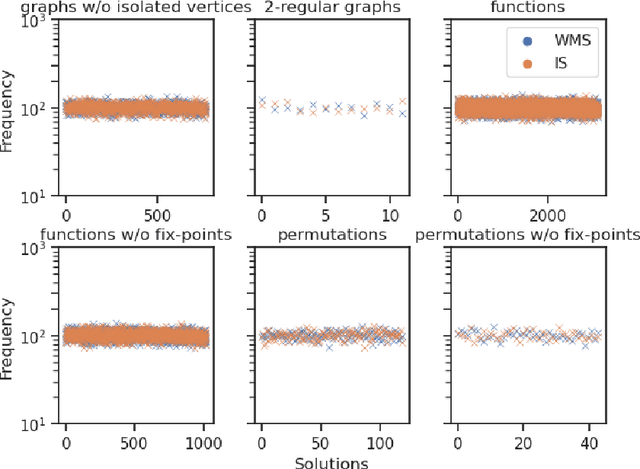
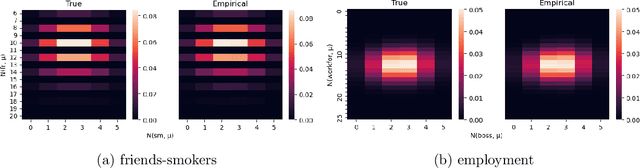
In this paper, we study the sampling problem for first-order logic proposed recently by Wang et al. -- how to efficiently sample a model of a given first-order sentence on a finite domain? We extend their result for the universally-quantified subfragment of two-variable logic $\mathbf{FO}^2$ ($\mathbf{UFO}^2$) to the entire fragment of $\mathbf{FO}^2$. Specifically, we prove the domain-liftability under sampling of $\mathbf{FO}^2$, meaning that there exists a sampling algorithm for $\mathbf{FO}^2$ that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of counting constraints, such as $\forall x\exists_{=k} y: \varphi(x,y)$ and $\exists_{=k} x\forall y: \varphi(x,y)$, for some quantifier-free formula $\varphi(x,y)$. Our proposed method is constructive, and the resulting sampling algorithms have potential applications in various areas, including the uniform generation of combinatorial structures and sampling in statistical-relational models such as Markov logic networks and probabilistic logic programs.

Complex Handwriting Trajectory Recovery: Evaluation Metrics and Algorithm

Many important tasks such as forensic signature verification, calligraphy synthesis, etc, rely on handwriting trajectory recovery of which, however, even an appropriate evaluation metric is still missing. Indeed, existing metrics only focus on the writing orders but overlook the fidelity of glyphs. Taking both facets into account, we come up with two new metrics, the adaptive intersection on union (AIoU) which eliminates the influence of various stroke widths, and the length-independent dynamic time warping (LDTW) which solves the trajectory-point alignment problem. After that, we then propose a novel handwriting trajectory recovery model named Parsing-and-tracing ENcoder-decoder Network (PEN-Net), in particular for characters with both complex glyph and long trajectory, which was believed very challenging. In the PEN-Net, a carefully designed double-stream parsing encoder parses the glyph structure, and a global tracing decoder overcomes the memory difficulty of long trajectory prediction. Our experiments demonstrate that the two new metrics AIoU and LDTW together can truly assess the quality of handwriting trajectory recovery and the proposed PEN-Net exhibits satisfactory performance in various complex-glyph languages including Chinese, Japanese and Indic.