On Exact Sampling in the Two-Variable Fragment of First-Order Logic
Paper and Code
Feb 06, 2023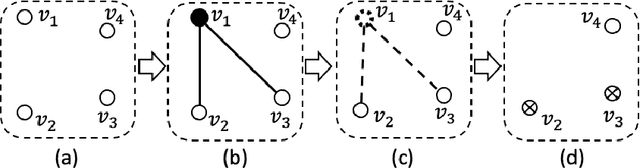
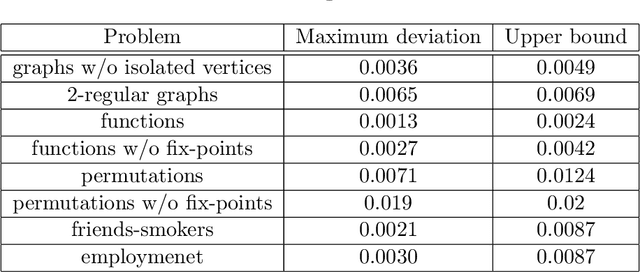
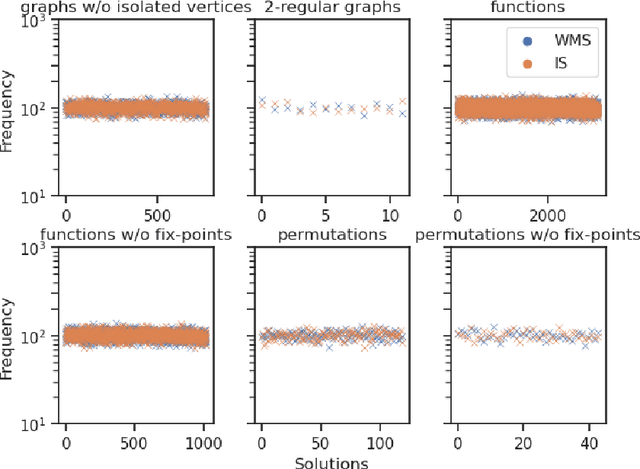
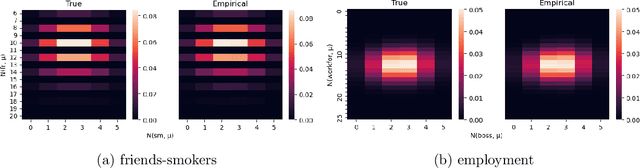
In this paper, we study the sampling problem for first-order logic proposed recently by Wang et al. -- how to efficiently sample a model of a given first-order sentence on a finite domain? We extend their result for the universally-quantified subfragment of two-variable logic $\mathbf{FO}^2$ ($\mathbf{UFO}^2$) to the entire fragment of $\mathbf{FO}^2$. Specifically, we prove the domain-liftability under sampling of $\mathbf{FO}^2$, meaning that there exists a sampling algorithm for $\mathbf{FO}^2$ that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of counting constraints, such as $\forall x\exists_{=k} y: \varphi(x,y)$ and $\exists_{=k} x\forall y: \varphi(x,y)$, for some quantifier-free formula $\varphi(x,y)$. Our proposed method is constructive, and the resulting sampling algorithms have potential applications in various areas, including the uniform generation of combinatorial structures and sampling in statistical-relational models such as Markov logic networks and probabilistic logic programs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge