Ondřej Kuželka
Tractable Weighted First-Order Model Counting with Bounded Treewidth Binary Evidence
Nov 12, 2025Abstract:The Weighted First-Order Model Counting Problem (WFOMC) asks to compute the weighted sum of models of a given first-order logic sentence over a given domain. Conditioning WFOMC on evidence -- fixing the truth values of a set of ground literals -- has been shown impossible in time polynomial in the domain size (unless $\mathsf{\#P \subseteq FP}$) even for fragments of logic that are otherwise tractable for WFOMC without evidence. In this work, we address the barrier by restricting the binary evidence to the case where the underlying Gaifman graph has bounded treewidth. We present a polynomial-time algorithm in the domain size for computing WFOMC for the two-variable fragments $\text{FO}^2$ and $\text{C}^2$ conditioned on such binary evidence. Furthermore, we show the applicability of our algorithm in combinatorial problems by solving the stable seating arrangement problem on bounded-treewidth graphs of bounded degree, which was an open problem. We also conducted experiments to show the scalability of our algorithm compared to the existing model counting solvers.
Model Enumeration of Two-Variable Logic with Quadratic Delay Complexity
May 26, 2025Abstract:We study the model enumeration problem of the function-free, finite domain fragment of first-order logic with two variables ($FO^2$). Specifically, given an $FO^2$ sentence $\Gamma$ and a positive integer $n$, how can one enumerate all the models of $\Gamma$ over a domain of size $n$? In this paper, we devise a novel algorithm to address this problem. The delay complexity, the time required between producing two consecutive models, of our algorithm is quadratic in the given domain size $n$ (up to logarithmic factors) when the sentence is fixed. This complexity is almost optimal since the interpretation of binary predicates in any model requires at least $\Omega(n^2)$ bits to represent.
Bridging Weighted First Order Model Counting and Graph Polynomials
Jul 16, 2024



Abstract:The Weighted First-Order Model Counting Problem (WFOMC) asks to compute the weighted sum of models of a given first-order logic sentence over a given domain. It can be solved in time polynomial in the domain size for sentences from the two-variable fragment with counting quantifiers, known as $C^2$. This polynomial-time complexity is also retained when extending $C^2$ by one of the following axioms: linear order axiom, tree axiom, forest axiom, directed acyclic graph axiom or connectedness axiom. An interesting question remains as to which other axioms can be added to the first-order sentences in this way. We provide a new perspective on this problem by associating WFOMC with graph polynomials. Using WFOMC, we define Weak Connectedness Polynomial and Strong Connectedness Polynomials for first-order logic sentences. It turns out that these polynomials have the following interesting properties. First, they can be computed in polynomial time in the domain size for sentences from $C^2$. Second, we can use them to solve WFOMC with all of the existing axioms known to be tractable as well as with new ones such as bipartiteness, strong connectedness, being a spanning subgraph, having $k$ connected components, etc. Third, the well-known Tutte polynomial can be recovered as a special case of the Weak Connectedness Polynomial, and the Strict and Non-Strict Directed Chromatic Polynomials can be recovered from the Strong Connectedness Polynomials, which allows us to show that these important graph polynomials can be computed in time polynomial in the number of vertices for any graph that can be encoded by a fixed $C^2$ sentence and a conjunction of an arbitrary number of ground unary literals.
Faster Repeated Evasion Attacks in Tree Ensembles
Feb 13, 2024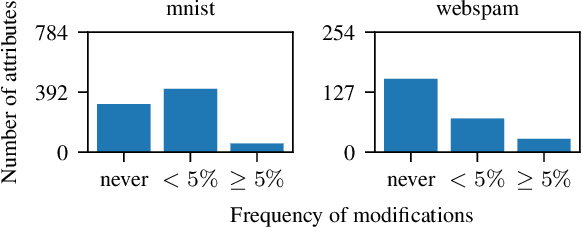
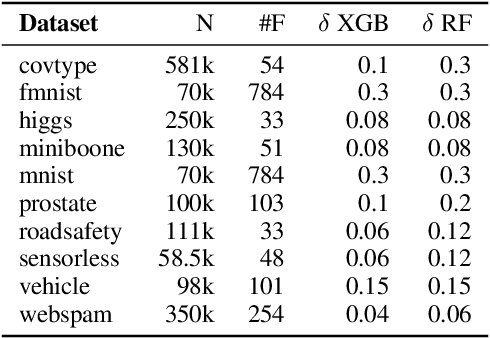
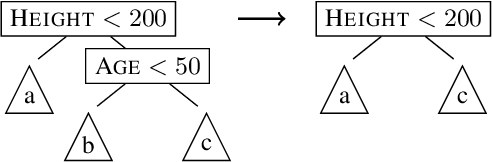
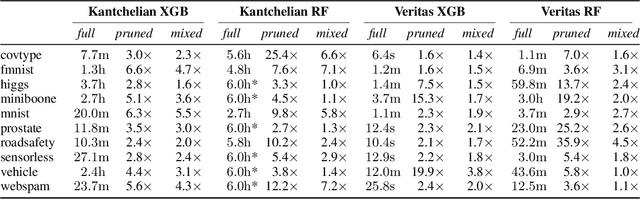
Abstract:Tree ensembles are one of the most widely used model classes. However, these models are susceptible to adversarial examples, i.e., slightly perturbed examples that elicit a misprediction. There has been significant research on designing approaches to construct such examples for tree ensembles. But this is a computationally challenging problem that often must be solved a large number of times (e.g., for all examples in a training set). This is compounded by the fact that current approaches attempt to find such examples from scratch. In contrast, we exploit the fact that multiple similar problems are being solved. Specifically, our approach exploits the insight that adversarial examples for tree ensembles tend to perturb a consistent but relatively small set of features. We show that we can quickly identify this set of features and use this knowledge to speedup constructing adversarial examples.
Lifted Algorithms for Symmetric Weighted First-Order Model Sampling
Aug 21, 2023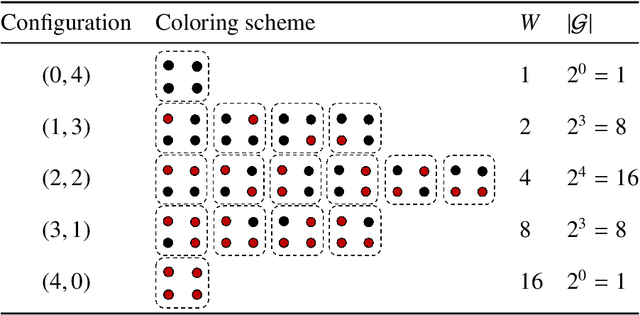
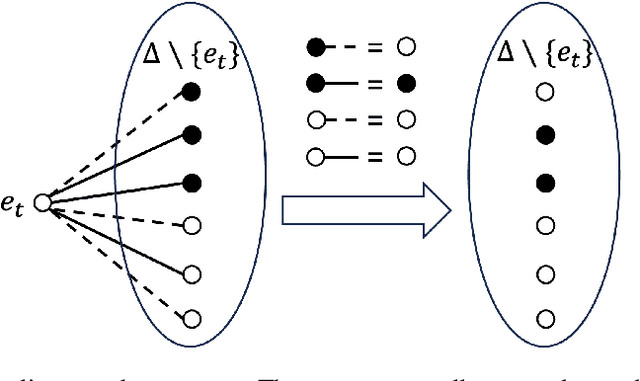

Abstract:Weighted model counting (WMC) is the task of computing the weighted sum of all satisfying assignments (i.e., models) of a propositional formula. Similarly, weighted model sampling (WMS) aims to randomly generate models with probability proportional to their respective weights. Both WMC and WMS are hard to solve exactly, falling under the $\#\mathsf{P}$-hard complexity class. However, it is known that the counting problem may sometimes be tractable, if the propositional formula can be compactly represented and expressed in first-order logic. In such cases, model counting problems can be solved in time polynomial in the domain size, and are known as domain-liftable. The following question then arises: Is it also the case for weighted model sampling? This paper addresses this question and answers it affirmatively. Specifically, we prove the domain-liftability under sampling for the two-variables fragment of first-order logic with counting quantifiers in this paper, by devising an efficient sampling algorithm for this fragment that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of cardinality constraints. To empirically verify our approach, we conduct experiments over various first-order formulas designed for the uniform generation of combinatorial structures and sampling in statistical-relational models. The results demonstrate that our algorithm outperforms a start-of-the-art WMS sampler by a substantial margin, confirming the theoretical results.
On Exact Sampling in the Two-Variable Fragment of First-Order Logic
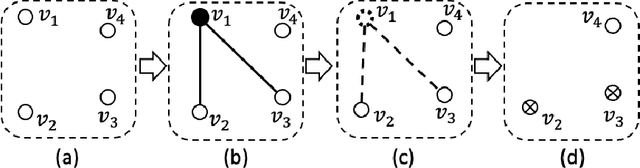
Feb 06, 2023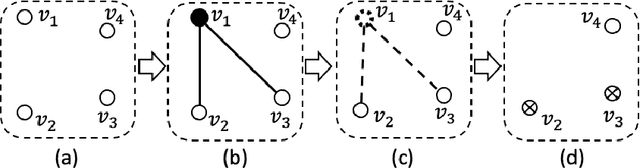
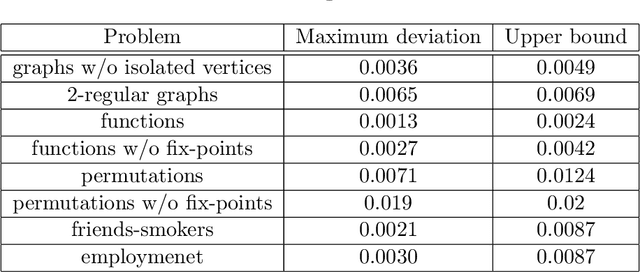
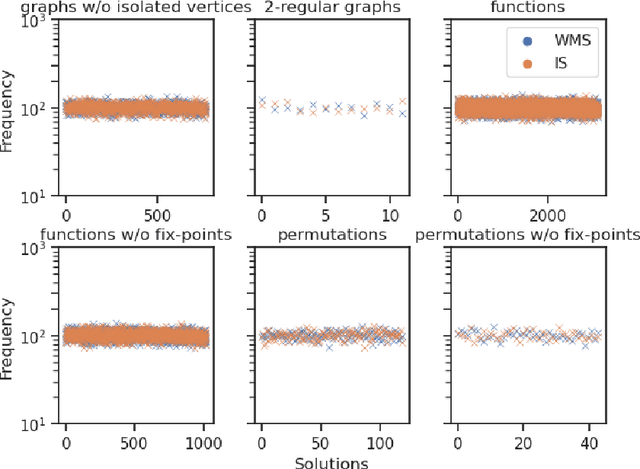
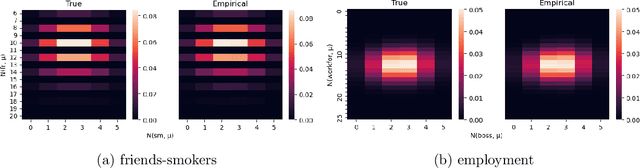
Abstract:In this paper, we study the sampling problem for first-order logic proposed recently by Wang et al. -- how to efficiently sample a model of a given first-order sentence on a finite domain? We extend their result for the universally-quantified subfragment of two-variable logic $\mathbf{FO}^2$ ($\mathbf{UFO}^2$) to the entire fragment of $\mathbf{FO}^2$. Specifically, we prove the domain-liftability under sampling of $\mathbf{FO}^2$, meaning that there exists a sampling algorithm for $\mathbf{FO}^2$ that runs in time polynomial in the domain size. We then further show that this result continues to hold even in the presence of counting constraints, such as $\forall x\exists_{=k} y: \varphi(x,y)$ and $\exists_{=k} x\forall y: \varphi(x,y)$, for some quantifier-free formula $\varphi(x,y)$. Our proposed method is constructive, and the resulting sampling algorithms have potential applications in various areas, including the uniform generation of combinatorial structures and sampling in statistical-relational models such as Markov logic networks and probabilistic logic programs.
Jump-Diffusion Langevin Dynamics for Multimodal Posterior Sampling
Nov 02, 2022Abstract:Bayesian methods of sampling from a posterior distribution are becoming increasingly popular due to their ability to precisely display the uncertainty of a model fit. Classical methods based on iterative random sampling and posterior evaluation such as Metropolis-Hastings are known to have desirable long run mixing properties, however are slow to converge. Gradient based methods, such as Langevin Dynamics (and its stochastic gradient counterpart) exhibit favorable dimension-dependence and fast mixing times for log-concave, and "close" to log-concave distributions, however also have long escape times from local minimizers. Many contemporary applications such as Bayesian Neural Networks are both high-dimensional and highly multimodal. In this paper we investigate the performance of a hybrid Metropolis and Langevin sampling method akin to Jump Diffusion on a range of synthetic and real data, indicating that careful calibration of mixing sampling jumps with gradient based chains significantly outperforms both pure gradient-based or sampling based schemes.
Lifted Inference with Linear Order Axiom
Nov 02, 2022Abstract:We consider the task of weighted first-order model counting (WFOMC) used for probabilistic inference in the area of statistical relational learning. Given a formula $\phi$, domain size $n$ and a pair of weight functions, what is the weighted sum of all models of $\phi$ over a domain of size $n$? It was shown that computing WFOMC of any logical sentence with at most two logical variables can be done in time polynomial in $n$. However, it was also shown that the task is $\texttt{#}P_1$-complete once we add the third variable, which inspired the search for extensions of the two-variable fragment that would still permit a running time polynomial in $n$. One of such extension is the two-variable fragment with counting quantifiers. In this paper, we prove that adding a linear order axiom (which forces one of the predicates in $\phi$ to introduce a linear ordering of the domain elements in each model of $\phi$) on top of the counting quantifiers still permits a computation time polynomial in the domain size. We present a new dynamic programming-based algorithm which can compute WFOMC with linear order in time polynomial in $n$, thus proving our primary claim.
Context-Specific Likelihood Weighting
Feb 09, 2021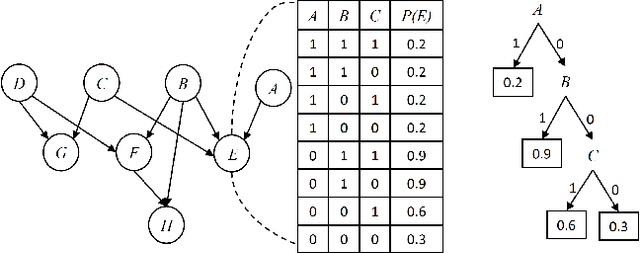



Abstract:Sampling is a popular method for approximate inference when exact inference is impractical. Generally, sampling algorithms do not exploit context-specific independence (CSI) properties of probability distributions. We introduce context-specific likelihood weighting (CS-LW), a new sampling methodology, which besides exploiting the classical conditional independence properties, also exploits CSI properties. Unlike the standard likelihood weighting, CS-LW is based on partial assignments of random variables and requires fewer samples for convergence due to the sampling variance reduction. Furthermore, the speed of generating samples increases. Our novel notion of contextual assignments theoretically justifies CS-LW. We empirically show that CS-LW is competitive with state-of-the-art algorithms for approximate inference in the presence of a significant amount of CSIs.
Neural Markov Logic Networks
May 31, 2019
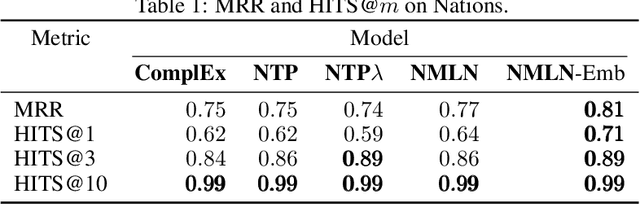

Abstract:We introduce Neural Markov Logic Networks (NMLNs), a statistical relational learning system that borrows ideas from Markov logic. Like Markov Logic Networks (MLNs), NMLNs are an exponential-family model for modelling distributions over possible worlds, but unlike MLNs, they do not rely on explicitly specified first-order logic rules. Instead, NMLNs learn an implicit representation of such rules as a neural network that acts as a potential function on fragments of the relational structure. Interestingly, any MLN can be represented as an NMLN. Similarly to recently proposed Neural theorem provers (NTPs) [Rockt\"aschel and Riedel, 2017], NMLNs can exploit embeddings of constants but, unlike NTPs, NMLNs work well also in their absence. This is extremely important for predicting in settings other than the transductive one. We showcase the potential of NMLNs on knowledge-base completion tasks and on generation of molecular (graph) data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge