Faster Repeated Evasion Attacks in Tree Ensembles

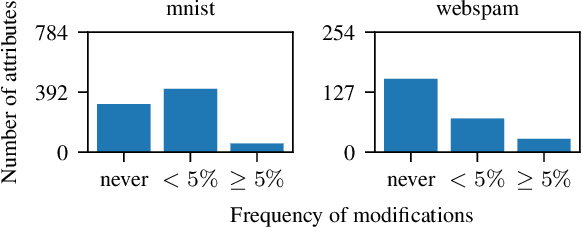
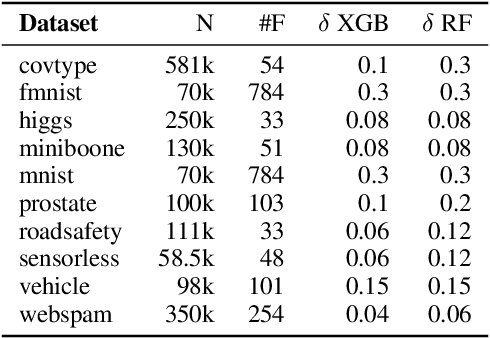
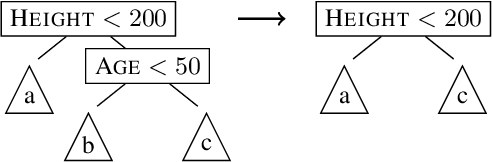
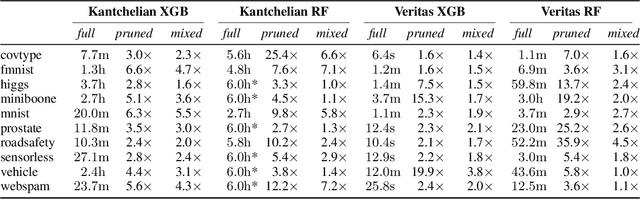
Tree ensembles are one of the most widely used model classes. However, these models are susceptible to adversarial examples, i.e., slightly perturbed examples that elicit a misprediction. There has been significant research on designing approaches to construct such examples for tree ensembles. But this is a computationally challenging problem that often must be solved a large number of times (e.g., for all examples in a training set). This is compounded by the fact that current approaches attempt to find such examples from scratch. In contrast, we exploit the fact that multiple similar problems are being solved. Specifically, our approach exploits the insight that adversarial examples for tree ensembles tend to perturb a consistent but relatively small set of features. We show that we can quickly identify this set of features and use this knowledge to speedup constructing adversarial examples.

Adversarial Example Detection in Deployed Tree Ensembles

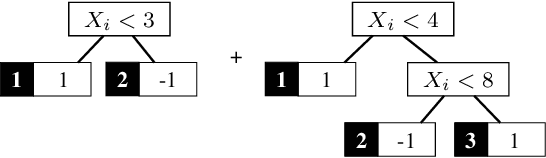
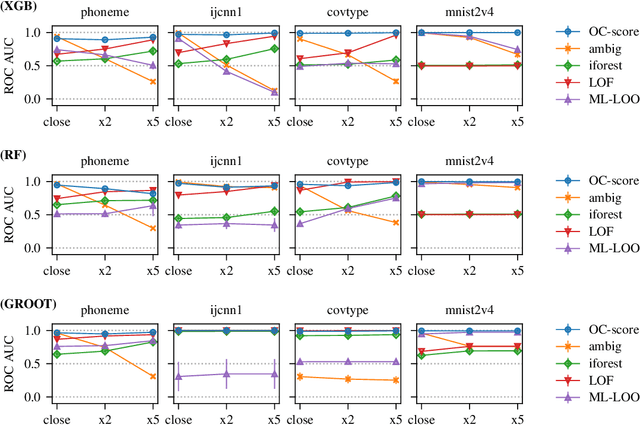
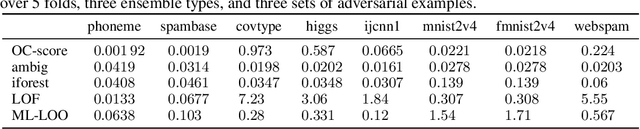
Tree ensembles are powerful models that are widely used. However, they are susceptible to adversarial examples, which are examples that purposely constructed to elicit a misprediction from the model. This can degrade performance and erode a user's trust in the model. Typically, approaches try to alleviate this problem by verifying how robust a learned ensemble is or robustifying the learning process. We take an alternative approach and attempt to detect adversarial examples in a post-deployment setting. We present a novel method for this task that works by analyzing an unseen example's output configuration, which is the set of predictions made by an ensemble's constituent trees. Our approach works with any additive tree ensemble and does not require training a separate model. We evaluate our approach on three different tree ensemble learners. We empirically show that our method is currently the best adversarial detection method for tree ensembles.

Versatile Verification of Tree Ensembles

Machine learned models often must abide by certain requirements (e.g., fairness or legal). This has spurred interested in developing approaches that can provably verify whether a model satisfies certain properties. This paper introduces a generic algorithm called Veritas that enables tackling multiple different verification tasks for tree ensemble models like random forests (RFs) and gradient boosting decision trees (GBDTs). This generality contrasts with previous work, which has focused exclusively on either adversarial example generation or robustness checking. Veritas formulates the verification task as a generic optimization problem and introduces a novel search space representation. Veritas offers two key advantages. First, it provides anytime lower and upper bounds when the optimization problem cannot be solved exactly. In contrast, many existing methods have focused on exact solutions and are thus limited by the verification problem being NP-complete. Second, Veritas produces full (bounded suboptimal) solutions that can be used to generate concrete examples. We experimentally show that Veritas outperforms the previous state of the art by (a) generating exact solutions more frequently, (b) producing tighter bounds when (a) is not possible, and (c) offering orders of magnitude speed ups. Subsequently, Veritas enables tackling more and larger real-world verification scenarios.

Additive Tree Ensembles: Reasoning About Potential Instances

Imagine being able to ask questions to a black box model such as "Which adversarial examples exist?", "Does a specific attribute have a disproportionate effect on the model's prediction?" or "What kind of predictions are possible for a partially described example?" This last question is particularly important if your partial description does not correspond to any observed example in your data, as it provides insight into how the model will extrapolate to unseen data. These capabilities would be extremely helpful as it would allow a user to better understand the model's behavior, particularly as it relates to issues such as robustness, fairness, and bias. In this paper, we propose such an approach for an ensemble of trees. Since, in general, this task is intractable we present a strategy that (1) can prune part of the input space given the question asked to simplify the problem; and (2) follows a divide and conquer approach that is incremental and can always return some answers and indicates which parts of the input domains are still uncertain. The usefulness of our approach is shown on a diverse set of use cases.