Erlin Pan
Attention Beyond Neighborhoods: Reviving Transformer for Graph Clustering
Sep 18, 2025Abstract:Attention mechanisms have become a cornerstone in modern neural networks, driving breakthroughs across diverse domains. However, their application to graph structured data, where capturing topological connections is essential, remains underexplored and underperforming compared to Graph Neural Networks (GNNs), particularly in the graph clustering task. GNN tends to overemphasize neighborhood aggregation, leading to a homogenization of node representations. Conversely, Transformer tends to over globalize, highlighting distant nodes at the expense of meaningful local patterns. This dichotomy raises a key question: Is attention inherently redundant for unsupervised graph learning? To address this, we conduct a comprehensive empirical analysis, uncovering the complementary weaknesses of GNN and Transformer in graph clustering. Motivated by these insights, we propose the Attentive Graph Clustering Network (AGCN) a novel architecture that reinterprets the notion that graph is attention. AGCN directly embeds the attention mechanism into the graph structure, enabling effective global information extraction while maintaining sensitivity to local topological cues. Our framework incorporates theoretical analysis to contrast AGCN behavior with GNN and Transformer and introduces two innovations: (1) a KV cache mechanism to improve computational efficiency, and (2) a pairwise margin contrastive loss to boost the discriminative capacity of the attention space. Extensive experimental results demonstrate that AGCN outperforms state-of-the-art methods.
Aggregation-aware MLP: An Unsupervised Approach for Graph Message-passing
Jul 27, 2025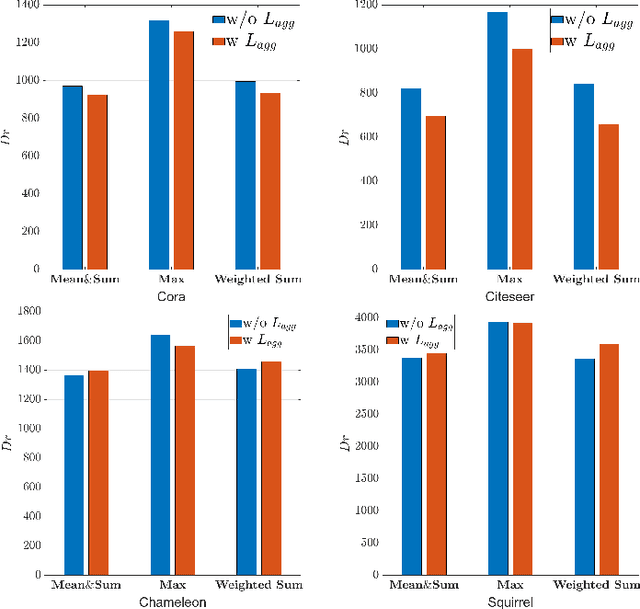

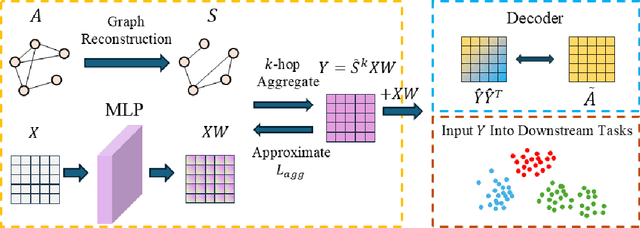
Abstract:Graph Neural Networks (GNNs) have become a dominant approach to learning graph representations, primarily because of their message-passing mechanisms. However, GNNs typically adopt a fixed aggregator function such as Mean, Max, or Sum without principled reasoning behind the selection. This rigidity, especially in the presence of heterophily, often leads to poor, problem dependent performance. Although some attempts address this by designing more sophisticated aggregation functions, these methods tend to rely heavily on labeled data, which is often scarce in real-world tasks. In this work, we propose a novel unsupervised framework, "Aggregation-aware Multilayer Perceptron" (AMLP), which shifts the paradigm from directly crafting aggregation functions to making MLP adaptive to aggregation. Our lightweight approach consists of two key steps: First, we utilize a graph reconstruction method that facilitates high-order grouping effects, and second, we employ a single-layer network to encode varying degrees of heterophily, thereby improving the capacity and applicability of the model. Extensive experiments on node clustering and classification demonstrate the superior performance of AMLP, highlighting its potential for diverse graph learning scenarios.
One Node One Model: Featuring the Missing-Half for Graph Clustering
Dec 13, 2024



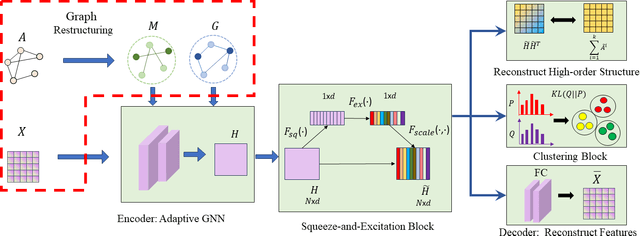
Abstract:Most existing graph clustering methods primarily focus on exploiting topological structure, often neglecting the ``missing-half" node feature information, especially how these features can enhance clustering performance. This issue is further compounded by the challenges associated with high-dimensional features. Feature selection in graph clustering is particularly difficult because it requires simultaneously discovering clusters and identifying the relevant features for these clusters. To address this gap, we introduce a novel paradigm called ``one node one model", which builds an exclusive model for each node and defines the node label as a combination of predictions for node groups. Specifically, the proposed ``Feature Personalized Graph Clustering (FPGC)" method identifies cluster-relevant features for each node using a squeeze-and-excitation block, integrating these features into each model to form the final representations. Additionally, the concept of feature cross is developed as a data augmentation technique to learn low-order feature interactions. Extensive experimental results demonstrate that FPGC outperforms state-of-the-art clustering methods. Moreover, the plug-and-play nature of our method provides a versatile solution to enhance GNN-based models from a feature perspective.
Provable Filter for Real-world Graph Clustering
Mar 06, 2024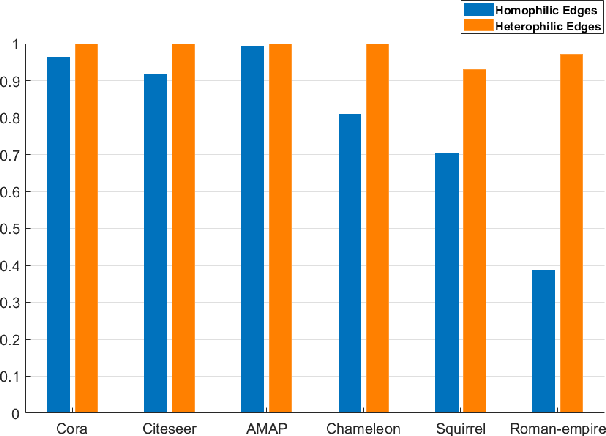
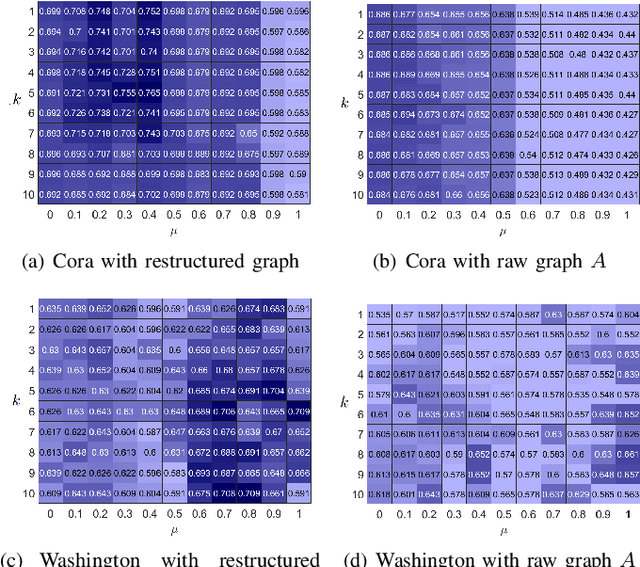
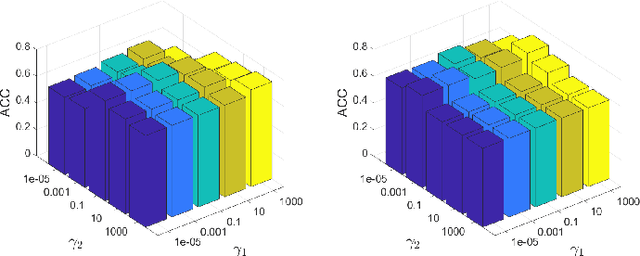
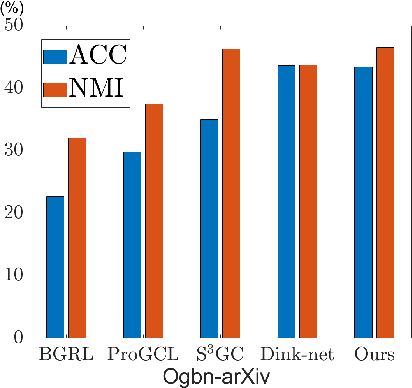
Abstract:Graph clustering, an important unsupervised problem, has been shown to be more resistant to advances in Graph Neural Networks (GNNs). In addition, almost all clustering methods focus on homophilic graphs and ignore heterophily. This significantly limits their applicability in practice, since real-world graphs exhibit a structural disparity and cannot simply be classified as homophily and heterophily. Thus, a principled way to handle practical graphs is urgently needed. To fill this gap, we provide a novel solution with theoretical support. Interestingly, we find that most homophilic and heterophilic edges can be correctly identified on the basis of neighbor information. Motivated by this finding, we construct two graphs that are highly homophilic and heterophilic, respectively. They are used to build low-pass and high-pass filters to capture holistic information. Important features are further enhanced by the squeeze-and-excitation block. We validate our approach through extensive experiments on both homophilic and heterophilic graphs. Empirical results demonstrate the superiority of our method compared to state-of-the-art clustering methods.
CDC: A Simple Framework for Complex Data Clustering
Mar 06, 2024



Abstract:In today's data-driven digital era, the amount as well as complexity, such as multi-view, non-Euclidean, and multi-relational, of the collected data are growing exponentially or even faster. Clustering, which unsupervisely extracts valid knowledge from data, is extremely useful in practice. However, existing methods are independently developed to handle one particular challenge at the expense of the others. In this work, we propose a simple but effective framework for complex data clustering (CDC) that can efficiently process different types of data with linear complexity. We first utilize graph filtering to fuse geometry structure and attribute information. We then reduce the complexity with high-quality anchors that are adaptively learned via a novel similarity-preserving regularizer. We illustrate the cluster-ability of our proposed method theoretically and experimentally. In particular, we deploy CDC to graph data of size 111M.
PC-Conv: Unifying Homophily and Heterophily with Two-fold Filtering
Dec 22, 2023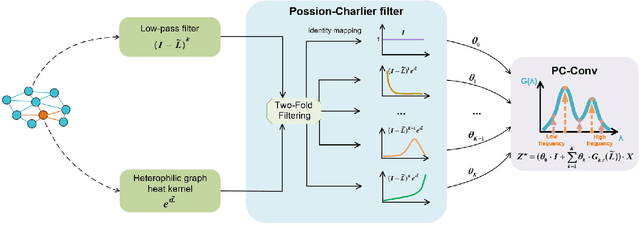
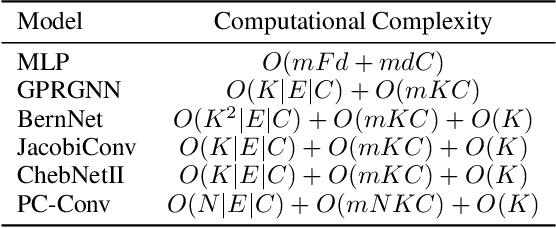
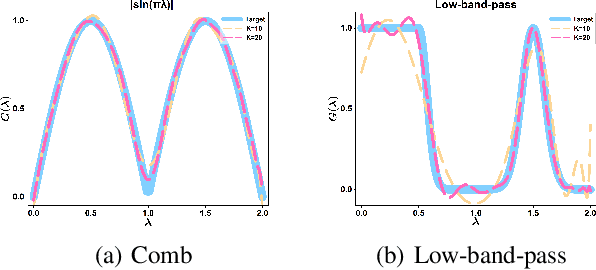

Abstract:Recently, many carefully crafted graph representation learning methods have achieved impressive performance on either strong heterophilic or homophilic graphs, but not both. Therefore, they are incapable of generalizing well across real-world graphs with different levels of homophily. This is attributed to their neglect of homophily in heterophilic graphs, and vice versa. In this paper, we propose a two-fold filtering mechanism to extract homophily in heterophilic graphs and vice versa. In particular, we extend the graph heat equation to perform heterophilic aggregation of global information from a long distance. The resultant filter can be exactly approximated by the Possion-Charlier (PC) polynomials. To further exploit information at multiple orders, we introduce a powerful graph convolution PC-Conv and its instantiation PCNet for the node classification task. Compared with state-of-the-art GNNs, PCNet shows competitive performance on well-known homophilic and heterophilic graphs. Our implementation is available at https://github.com/uestclbh/PC-Conv.
Beyond Homophily: Reconstructing Structure for Graph-agnostic Clustering
May 03, 2023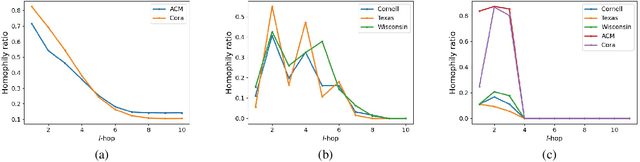
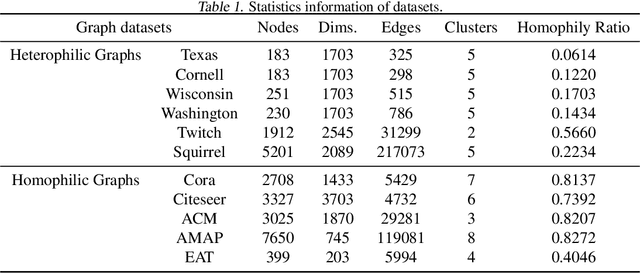
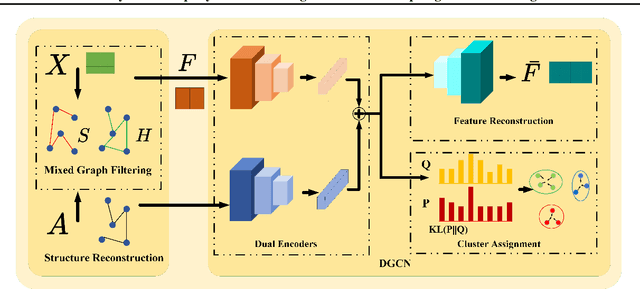
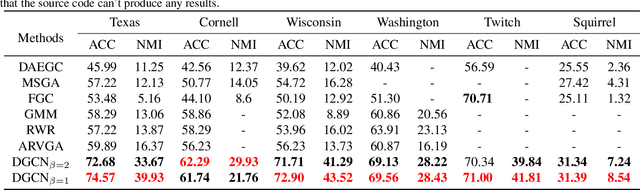
Abstract:Graph neural networks (GNNs) based methods have achieved impressive performance on node clustering task. However, they are designed on the homophilic assumption of graph and clustering on heterophilic graph is overlooked. Due to the lack of labels, it is impossible to first identify a graph as homophilic or heterophilic before a suitable GNN model can be found. Hence, clustering on real-world graph with various levels of homophily poses a new challenge to the graph research community. To fill this gap, we propose a novel graph clustering method, which contains three key components: graph reconstruction, a mixed filter, and dual graph clustering network. To be graph-agnostic, we empirically construct two graphs which are high homophily and heterophily from each data. The mixed filter based on the new graphs extracts both low-frequency and high-frequency information. To reduce the adverse coupling between node attribute and topological structure, we separately map them into two subspaces in dual graph clustering network. Extensive experiments on 11 benchmark graphs demonstrate our promising performance. In particular, our method dominates others on heterophilic graphs.
High-order Multi-view Clustering for Generic Data
Sep 22, 2022
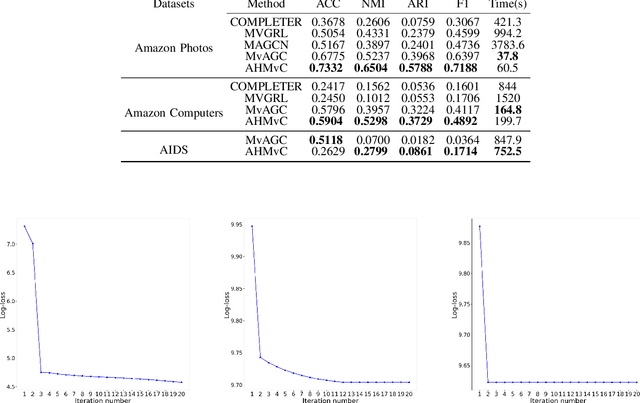
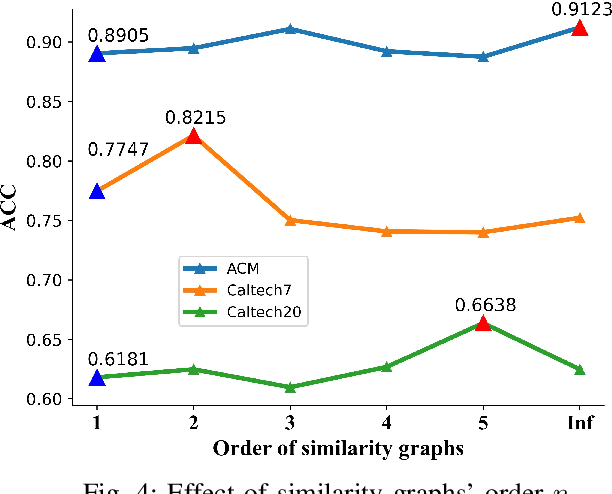
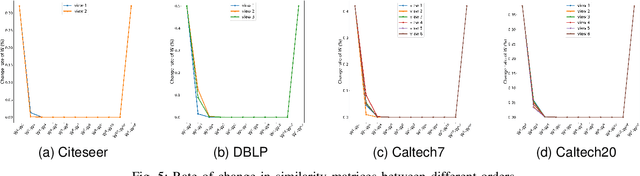
Abstract:Graph-based multi-view clustering has achieved better performance than most non-graph approaches. However, in many real-world scenarios, the graph structure of data is not given or the quality of initial graph is poor. Additionally, existing methods largely neglect the high-order neighborhood information that characterizes complex intrinsic interactions. To tackle these problems, we introduce an approach called high-order multi-view clustering (HMvC) to explore the topology structure information of generic data. Firstly, graph filtering is applied to encode structure information, which unifies the processing of attributed graph data and non-graph data in a single framework. Secondly, up to infinity-order intrinsic relationships are exploited to enrich the learned graph. Thirdly, to explore the consistent and complementary information of various views, an adaptive graph fusion mechanism is proposed to achieve a consensus graph. Comprehensive experimental results on both non-graph and attributed graph data show the superior performance of our method with respect to various state-of-the-art techniques, including some deep learning methods.
Multi-view Contrastive Graph Clustering
Oct 22, 2021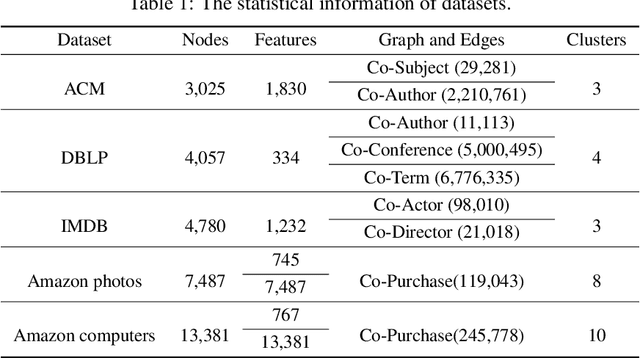
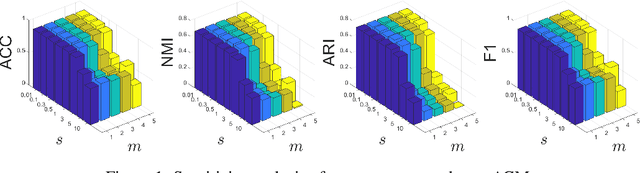
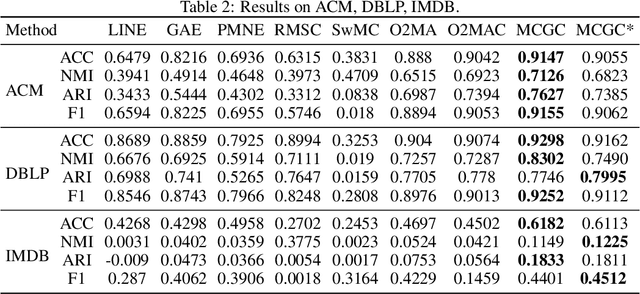
Abstract:With the explosive growth of information technology, multi-view graph data have become increasingly prevalent and valuable. Most existing multi-view clustering techniques either focus on the scenario of multiple graphs or multi-view attributes. In this paper, we propose a generic framework to cluster multi-view attributed graph data. Specifically, inspired by the success of contrastive learning, we propose multi-view contrastive graph clustering (MCGC) method to learn a consensus graph since the original graph could be noisy or incomplete and is not directly applicable. Our method composes of two key steps: we first filter out the undesirable high-frequency noise while preserving the graph geometric features via graph filtering and obtain a smooth representation of nodes; we then learn a consensus graph regularized by graph contrastive loss. Results on several benchmark datasets show the superiority of our method with respect to state-of-the-art approaches. In particular, our simple approach outperforms existing deep learning-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge