Entropy-Guided Dynamic Tokens for Graph-LLM Alignment in Molecular Understanding

Molecular understanding is central to advancing areas such as scientific discovery, yet Large Language Models (LLMs) struggle to understand molecular graphs effectively. Existing graph-LLM bridges often adapt the Q-Former-style connector with fixed-length static tokens, which is originally designed for vision tasks. These designs overlook stereochemistry and substructural context and typically require costly LLM-backbone fine-tuning, limiting efficiency and generalization. We introduce EDT-Former, an Entropy-guided Dynamic Token Transformer that generates tokens aligned with informative molecular patches, thereby preserving both local and global structural features for molecular graph understanding. Beyond prior approaches, EDT-Former enables alignment between frozen graph encoders and LLMs without tuning the LLM backbone (excluding the embedding layer), resulting in computationally efficient finetuning, and achieves stateof-the-art results on MoleculeQA, Molecule-oriented Mol-Instructions, and property prediction benchmarks (TDC, MoleculeNet), underscoring its effectiveness for scalable and generalizable multimodal molecular understanding

Scaling-Aware Adapter for Structure-Grounded LLM Reasoning

Large language models (LLMs) are enabling reasoning over biomolecular structures, yet existing methods remain modality-specific and typically compress structural inputs through sequence-based tokenization or fixed-length query connectors. Such architectures either omit the geometric groundings requisite for mitigating structural hallucinations or impose inflexible modality fusion bottlenecks that concurrently over-compress and suboptimally allocate structural tokens, thereby impeding the realization of generalized all-atom reasoning. We introduce Cuttlefish, a unified all-atom LLM that grounds language reasoning in geometric cues while scaling modality tokens with structural complexity. First, Scaling-Aware Patching leverages an instruction-conditioned gating mechanism to generate variable-size patches over structural graphs, adaptively scaling the query token budget with structural complexity to mitigate fixed-length connector bottlenecks. Second, Geometry Grounding Adapter refines these adaptive tokens via cross-attention to modality embeddings and injects the resulting modality tokens into the LLM, exposing explicit geometric cues to reduce structural hallucination. Experiments across diverse all-atom benchmarks demonstrate that Cuttlefish achieves superior performance in heterogeneous structure-grounded reasoning. Code is available at the project repository.

Homophily Enhanced Graph Domain Adaptation

Graph Domain Adaptation (GDA) transfers knowledge from labeled source graphs to unlabeled target graphs, addressing the challenge of label scarcity. In this paper, we highlight the significance of graph homophily, a pivotal factor for graph domain alignment, which, however, has long been overlooked in existing approaches. Specifically, our analysis first reveals that homophily discrepancies exist in benchmarks. Moreover, we also show that homophily discrepancies degrade GDA performance from both empirical and theoretical aspects, which further underscores the importance of homophily alignment in GDA. Inspired by this finding, we propose a novel homophily alignment algorithm that employs mixed filters to smooth graph signals, thereby effectively capturing and mitigating homophily discrepancies between graphs. Experimental results on a variety of benchmarks verify the effectiveness of our method.

Leveraging Group Classification with Descending Soft Labeling for Deep Imbalanced Regression

Deep imbalanced regression (DIR), where the target values have a highly skewed distribution and are also continuous, is an intriguing yet under-explored problem in machine learning. While recent works have already shown that incorporating various classification-based regularizers can produce enhanced outcomes, the role of classification remains elusive in DIR. Moreover, such regularizers (e.g., contrastive penalties) merely focus on learning discriminative features of data, which inevitably results in ignorance of either continuity or similarity across the data. To address these issues, we first bridge the connection between the objectives of DIR and classification from a Bayesian perspective. Consequently, this motivates us to decompose the objective of DIR into a combination of classification and regression tasks, which naturally guides us toward a divide-and-conquer manner to solve the DIR problem. Specifically, by aggregating the data at nearby labels into the same groups, we introduce an ordinal group-aware contrastive learning loss along with a multi-experts regressor to tackle the different groups of data thereby maintaining the data continuity. Meanwhile, considering the similarity between the groups, we also propose a symmetric descending soft labeling strategy to exploit the intrinsic similarity across the data, which allows classification to facilitate regression more effectively. Extensive experiments on real-world datasets also validate the effectiveness of our method.

Simplified PCNet with Robustness

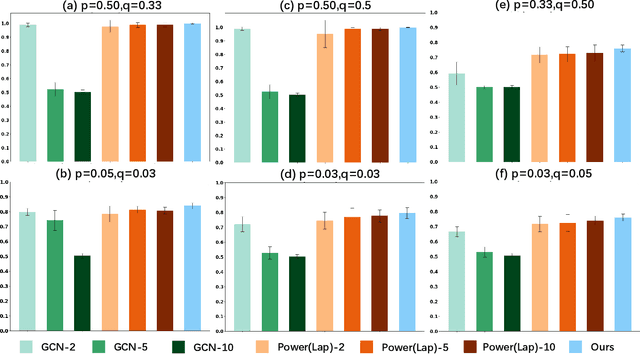
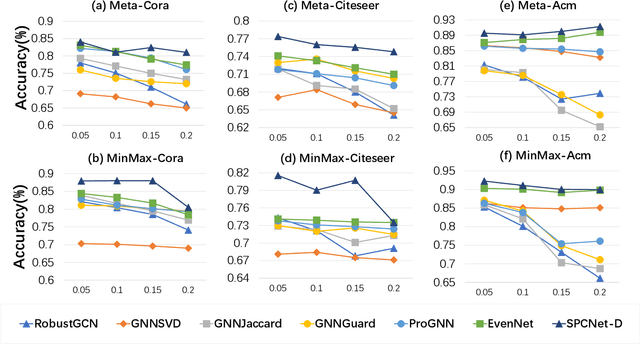
Graph Neural Networks (GNNs) have garnered significant attention for their success in learning the representation of homophilic or heterophilic graphs. However, they cannot generalize well to real-world graphs with different levels of homophily. In response, the Possion-Charlier Network (PCNet) \cite{li2024pc}, the previous work, allows graph representation to be learned from heterophily to homophily. Although PCNet alleviates the heterophily issue, there remain some challenges in further improving the efficacy and efficiency. In this paper, we simplify PCNet and enhance its robustness. We first extend the filter order to continuous values and reduce its parameters. Two variants with adaptive neighborhood sizes are implemented. Theoretical analysis shows our model's robustness to graph structure perturbations or adversarial attacks. We validate our approach through semi-supervised learning tasks on various datasets representing both homophilic and heterophilic graphs.

Structure-Preserving Graph Representation Learning

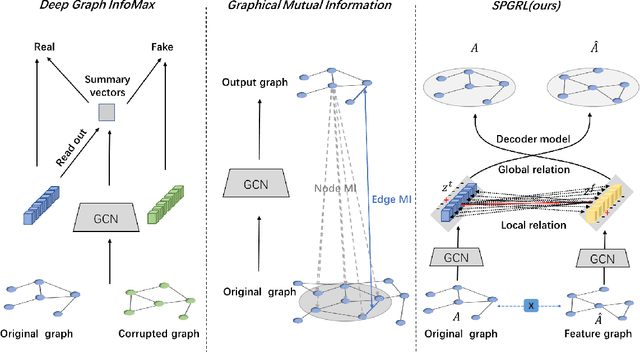
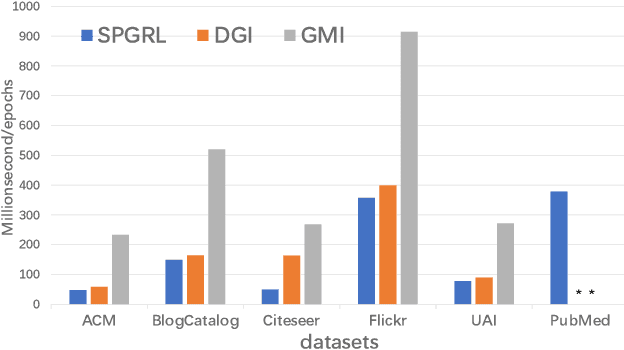
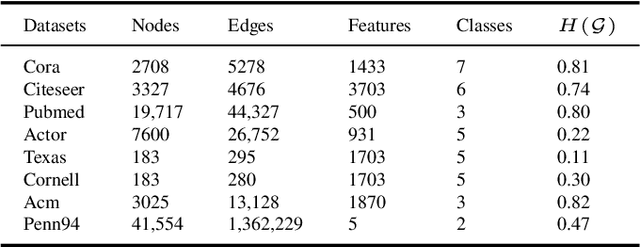
Though graph representation learning (GRL) has made significant progress, it is still a challenge to extract and embed the rich topological structure and feature information in an adequate way. Most existing methods focus on local structure and fail to fully incorporate the global topological structure. To this end, we propose a novel Structure-Preserving Graph Representation Learning (SPGRL) method, to fully capture the structure information of graphs. Specifically, to reduce the uncertainty and misinformation of the original graph, we construct a feature graph as a complementary view via k-Nearest Neighbor method. The feature graph can be used to contrast at node-level to capture the local relation. Besides, we retain the global topological structure information by maximizing the mutual information (MI) of the whole graph and feature embeddings, which is theoretically reduced to exchanging the feature embeddings of the feature and the original graphs to reconstruct themselves. Extensive experiments show that our method has quite superior performance on semi-supervised node classification task and excellent robustness under noise perturbation on graph structure or node features.