Simplified PCNet with Robustness
Paper and Code
Mar 06, 2024
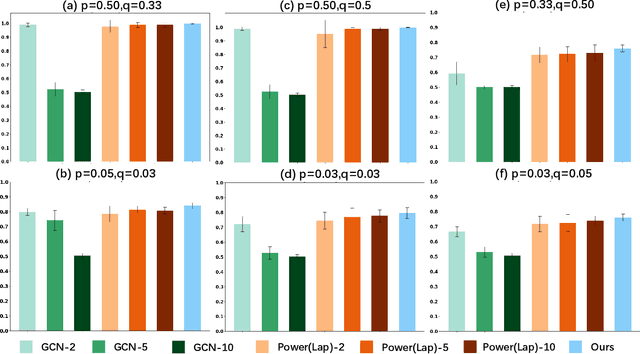
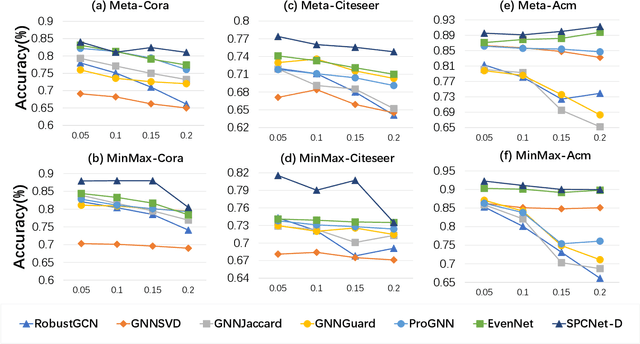
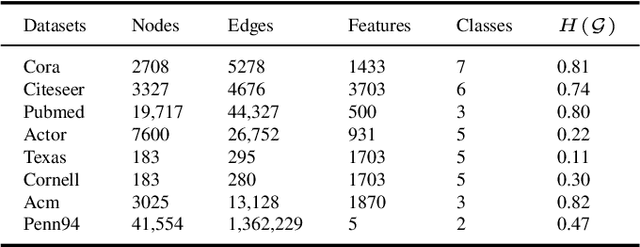
Graph Neural Networks (GNNs) have garnered significant attention for their success in learning the representation of homophilic or heterophilic graphs. However, they cannot generalize well to real-world graphs with different levels of homophily. In response, the Possion-Charlier Network (PCNet) \cite{li2024pc}, the previous work, allows graph representation to be learned from heterophily to homophily. Although PCNet alleviates the heterophily issue, there remain some challenges in further improving the efficacy and efficiency. In this paper, we simplify PCNet and enhance its robustness. We first extend the filter order to continuous values and reduce its parameters. Two variants with adaptive neighborhood sizes are implemented. Theoretical analysis shows our model's robustness to graph structure perturbations or adversarial attacks. We validate our approach through semi-supervised learning tasks on various datasets representing both homophilic and heterophilic graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge