Causal Representation Learning from Multimodal Biological Observations

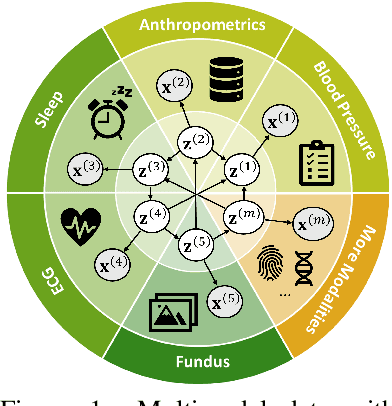
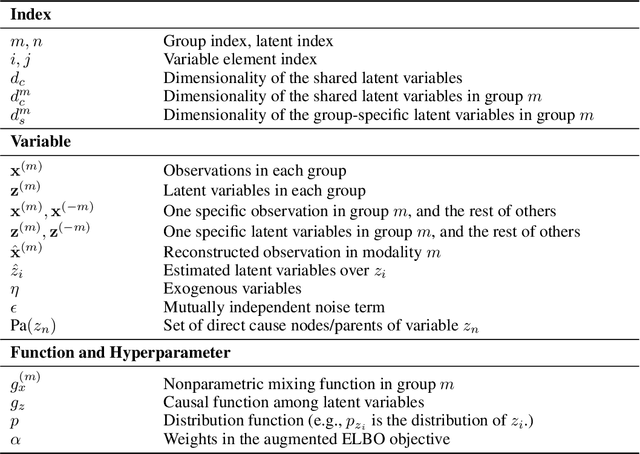
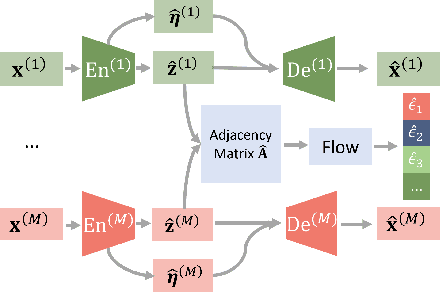
Prevalent in biological applications (e.g., human phenotype measurements), multimodal datasets can provide valuable insights into the underlying biological mechanisms. However, current machine learning models designed to analyze such datasets still lack interpretability and theoretical guarantees, which are essential to biological applications. Recent advances in causal representation learning have shown promise in uncovering the interpretable latent causal variables with formal theoretical certificates. Unfortunately, existing works for multimodal distributions either rely on restrictive parametric assumptions or provide rather coarse identification results, limiting their applicability to biological research which favors a detailed understanding of the mechanisms. In this work, we aim to develop flexible identification conditions for multimodal data and principled methods to facilitate the understanding of biological datasets. Theoretically, we consider a flexible nonparametric latent distribution (c.f., parametric assumptions in prior work) permitting causal relationships across potentially different modalities. We establish identifiability guarantees for each latent component, extending the subspace identification results from prior work. Our key theoretical ingredient is the structural sparsity of the causal connections among distinct modalities, which, as we will discuss, is natural for a large collection of biological systems. Empirically, we propose a practical framework to instantiate our theoretical insights. We demonstrate the effectiveness of our approach through extensive experiments on both numerical and synthetic datasets. Results on a real-world human phenotype dataset are consistent with established medical research, validating our theoretical and methodological framework.

$ψ$DAG: Projected Stochastic Approximation Iteration for DAG Structure Learning

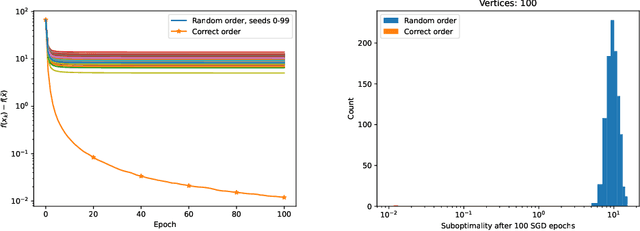
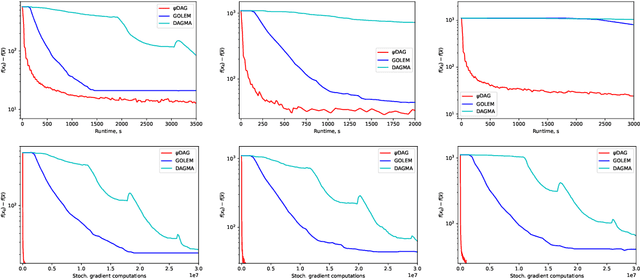
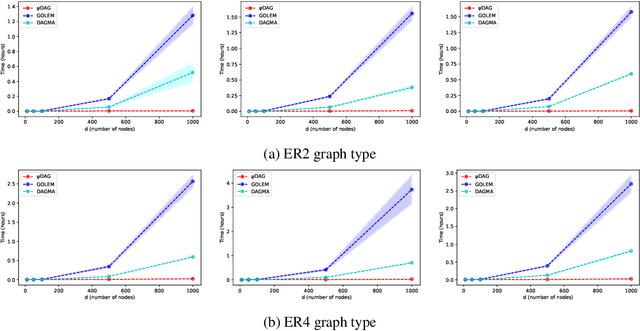
Learning the structure of Directed Acyclic Graphs (DAGs) presents a significant challenge due to the vast combinatorial search space of possible graphs, which scales exponentially with the number of nodes. Recent advancements have redefined this problem as a continuous optimization task by incorporating differentiable acyclicity constraints. These methods commonly rely on algebraic characterizations of DAGs, such as matrix exponentials, to enable the use of gradient-based optimization techniques. Despite these innovations, existing methods often face optimization difficulties due to the highly non-convex nature of DAG constraints and the per-iteration computational complexity. In this work, we present a novel framework for learning DAGs, employing a Stochastic Approximation approach integrated with Stochastic Gradient Descent (SGD)-based optimization techniques. Our framework introduces new projection methods tailored to efficiently enforce DAG constraints, ensuring that the algorithm converges to a feasible local minimum. With its low iteration complexity, the proposed method is well-suited for handling large-scale problems with improved computational efficiency. We demonstrate the effectiveness and scalability of our framework through comprehensive experimental evaluations, which confirm its superior performance across various settings.

Confidence Matters: Revisiting Intrinsic Self-Correction Capabilities of Large Language Models

The recent success of Large Language Models (LLMs) has catalyzed an increasing interest in their self-correction capabilities. This paper presents a comprehensive investigation into the intrinsic self-correction of LLMs, attempting to address the ongoing debate about its feasibility. Our research has identified an important latent factor - the "confidence" of LLMs - during the self-correction process. Overlooking this factor may cause the models to over-criticize themselves, resulting in unreliable conclusions regarding the efficacy of self-correction. We have experimentally observed that LLMs possess the capability to understand the "confidence" in their own responses. It motivates us to develop an "If-or-Else" (IoE) prompting framework, designed to guide LLMs in assessing their own "confidence", facilitating intrinsic self-corrections. We conduct extensive experiments and demonstrate that our IoE-based Prompt can achieve a consistent improvement regarding the accuracy of self-corrected responses over the initial answers. Our study not only sheds light on the underlying factors affecting self-correction in LLMs, but also introduces a practical framework that utilizes the IoE prompting principle to efficiently improve self-correction capabilities with "confidence". The code is available at https://github.com/MBZUAI-CLeaR/IoE-Prompting.git.

Federated Causal Discovery from Heterogeneous Data

Conventional causal discovery methods rely on centralized data, which is inconsistent with the decentralized nature of data in many real-world situations. This discrepancy has motivated the development of federated causal discovery (FCD) approaches. However, existing FCD methods may be limited by their potentially restrictive assumptions of identifiable functional causal models or homogeneous data distributions, narrowing their applicability in diverse scenarios. In this paper, we propose a novel FCD method attempting to accommodate arbitrary causal models and heterogeneous data. We first utilize a surrogate variable corresponding to the client index to account for the data heterogeneity across different clients. We then develop a federated conditional independence test (FCIT) for causal skeleton discovery and establish a federated independent change principle (FICP) to determine causal directions. These approaches involve constructing summary statistics as a proxy of the raw data to protect data privacy. Owing to the nonparametric properties, FCIT and FICP make no assumption about particular functional forms, thereby facilitating the handling of arbitrary causal models. We conduct extensive experiments on synthetic and real datasets to show the efficacy of our method. The code is available at https://github.com/lokali/FedCDH.git.