Causal Representation Learning from Multimodal Biological Observations
Paper and Code
Nov 10, 2024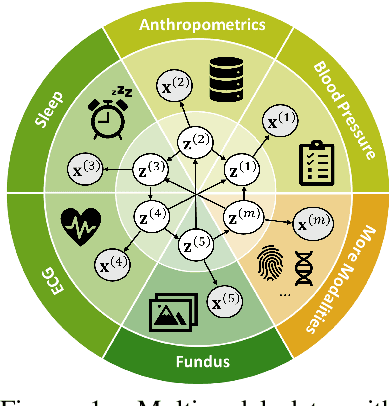

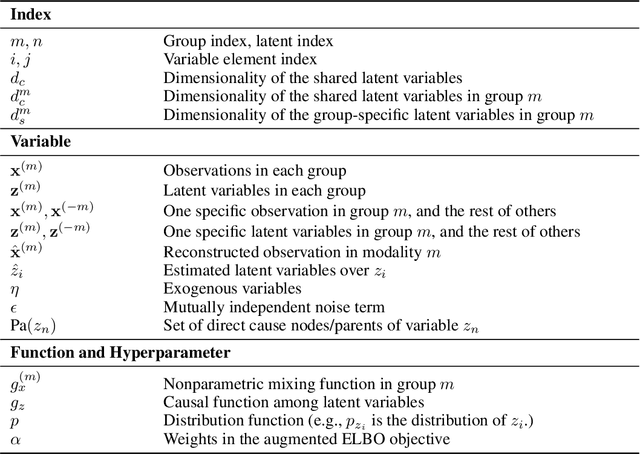
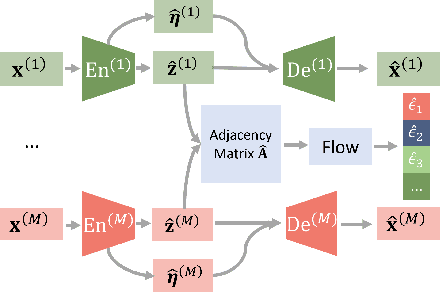
Prevalent in biological applications (e.g., human phenotype measurements), multimodal datasets can provide valuable insights into the underlying biological mechanisms. However, current machine learning models designed to analyze such datasets still lack interpretability and theoretical guarantees, which are essential to biological applications. Recent advances in causal representation learning have shown promise in uncovering the interpretable latent causal variables with formal theoretical certificates. Unfortunately, existing works for multimodal distributions either rely on restrictive parametric assumptions or provide rather coarse identification results, limiting their applicability to biological research which favors a detailed understanding of the mechanisms. In this work, we aim to develop flexible identification conditions for multimodal data and principled methods to facilitate the understanding of biological datasets. Theoretically, we consider a flexible nonparametric latent distribution (c.f., parametric assumptions in prior work) permitting causal relationships across potentially different modalities. We establish identifiability guarantees for each latent component, extending the subspace identification results from prior work. Our key theoretical ingredient is the structural sparsity of the causal connections among distinct modalities, which, as we will discuss, is natural for a large collection of biological systems. Empirically, we propose a practical framework to instantiate our theoretical insights. We demonstrate the effectiveness of our approach through extensive experiments on both numerical and synthetic datasets. Results on a real-world human phenotype dataset are consistent with established medical research, validating our theoretical and methodological framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge