Causal Representation Learning from Multimodal Biological Observations

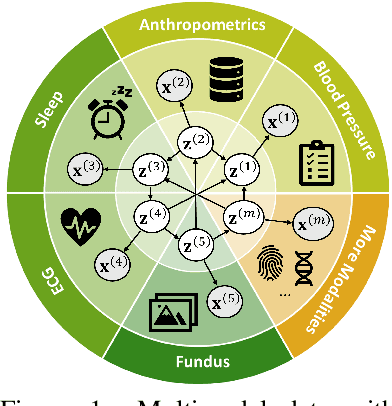
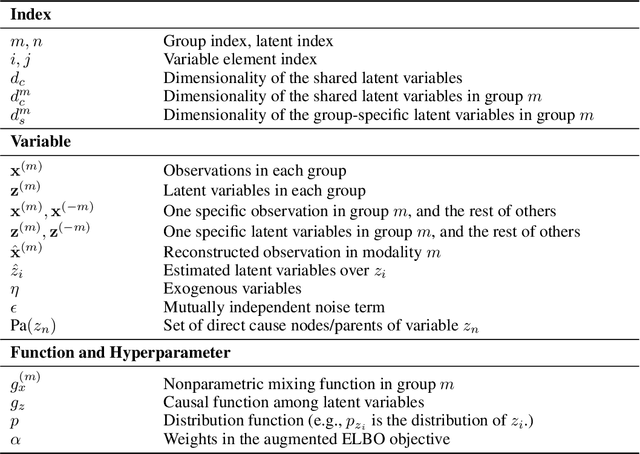
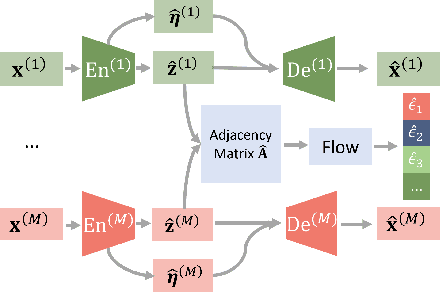
Prevalent in biological applications (e.g., human phenotype measurements), multimodal datasets can provide valuable insights into the underlying biological mechanisms. However, current machine learning models designed to analyze such datasets still lack interpretability and theoretical guarantees, which are essential to biological applications. Recent advances in causal representation learning have shown promise in uncovering the interpretable latent causal variables with formal theoretical certificates. Unfortunately, existing works for multimodal distributions either rely on restrictive parametric assumptions or provide rather coarse identification results, limiting their applicability to biological research which favors a detailed understanding of the mechanisms. In this work, we aim to develop flexible identification conditions for multimodal data and principled methods to facilitate the understanding of biological datasets. Theoretically, we consider a flexible nonparametric latent distribution (c.f., parametric assumptions in prior work) permitting causal relationships across potentially different modalities. We establish identifiability guarantees for each latent component, extending the subspace identification results from prior work. Our key theoretical ingredient is the structural sparsity of the causal connections among distinct modalities, which, as we will discuss, is natural for a large collection of biological systems. Empirically, we propose a practical framework to instantiate our theoretical insights. We demonstrate the effectiveness of our approach through extensive experiments on both numerical and synthetic datasets. Results on a real-world human phenotype dataset are consistent with established medical research, validating our theoretical and methodological framework.

Gene Regulatory Network Inference in the Presence of Dropouts: a Causal View

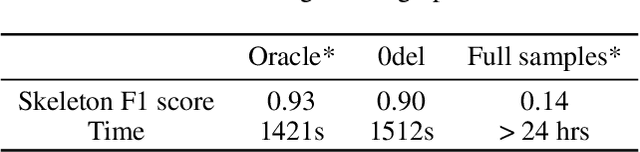
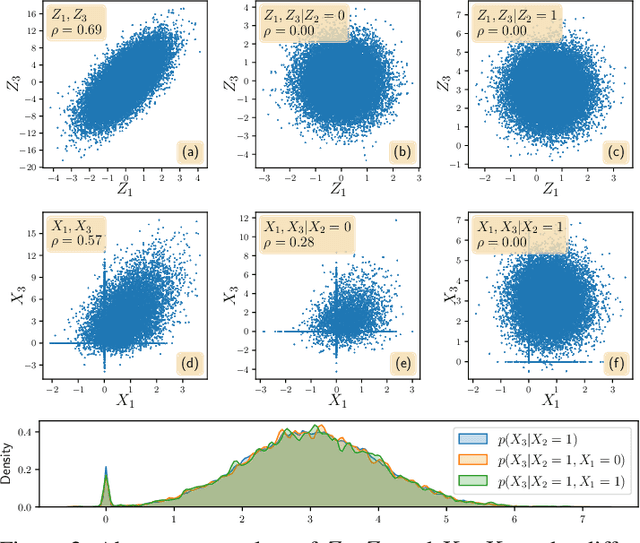
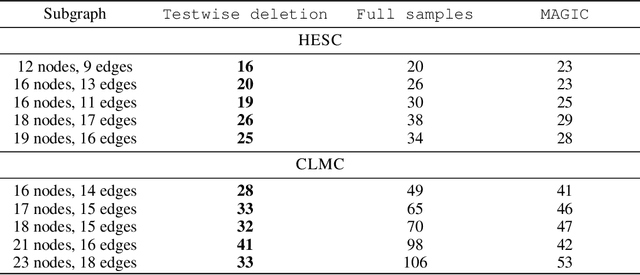
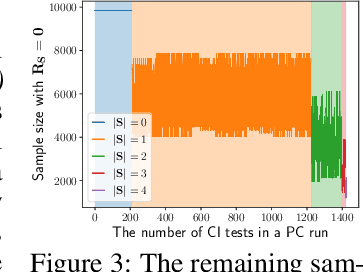
Gene regulatory network inference (GRNI) is a challenging problem, particularly owing to the presence of zeros in single-cell RNA sequencing data: some are biological zeros representing no gene expression, while some others are technical zeros arising from the sequencing procedure (aka dropouts), which may bias GRNI by distorting the joint distribution of the measured gene expressions. Existing approaches typically handle dropout error via imputation, which may introduce spurious relations as the true joint distribution is generally unidentifiable. To tackle this issue, we introduce a causal graphical model to characterize the dropout mechanism, namely, Causal Dropout Model. We provide a simple yet effective theoretical result: interestingly, the conditional independence (CI) relations in the data with dropouts, after deleting the samples with zero values (regardless if technical or not) for the conditioned variables, are asymptotically identical to the CI relations in the original data without dropouts. This particular test-wise deletion procedure, in which we perform CI tests on the samples without zeros for the conditioned variables, can be seamlessly integrated with existing structure learning approaches including constraint-based and greedy score-based methods, thus giving rise to a principled framework for GRNI in the presence of dropouts. We further show that the causal dropout model can be validated from data, and many existing statistical models to handle dropouts fit into our model as specific parametric instances. Empirical evaluation on synthetic, curated, and real-world experimental transcriptomic data comprehensively demonstrate the efficacy of our method.

Partial Identifiability for Domain Adaptation

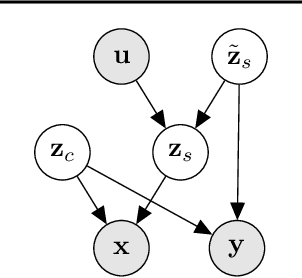
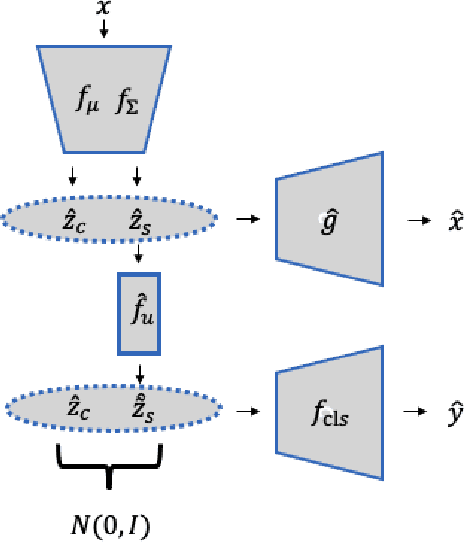
Unsupervised domain adaptation is critical to many real-world applications where label information is unavailable in the target domain. In general, without further assumptions, the joint distribution of the features and the label is not identifiable in the target domain. To address this issue, we rely on the property of minimal changes of causal mechanisms across domains to minimize unnecessary influences of distribution shifts. To encode this property, we first formulate the data-generating process using a latent variable model with two partitioned latent subspaces: invariant components whose distributions stay the same across domains and sparse changing components that vary across domains. We further constrain the domain shift to have a restrictive influence on the changing components. Under mild conditions, we show that the latent variables are partially identifiable, from which it follows that the joint distribution of data and labels in the target domain is also identifiable. Given the theoretical insights, we propose a practical domain adaptation framework called iMSDA. Extensive experimental results reveal that iMSDA outperforms state-of-the-art domain adaptation algorithms on benchmark datasets, demonstrating the effectiveness of our framework.

Domain Adaptation As a Problem of Inference on Graphical Models

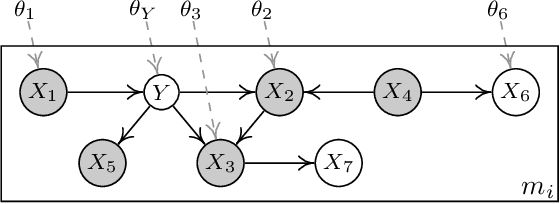
This paper is concerned with data-driven unsupervised domain adaptation, where it is unknown in advance how the joint distribution changes across domains, i.e., what factors or modules of the data distribution remain invariant or change across domains. To develop an automated way of domain adaptation with multiple source domains, we propose to use a graphical model as a compact way to encode the change property of the joint distribution, which can be learned from data, and then view domain adaptation as a problem of Bayesian inference on the graphical models. Such a graphical model distinguishes between constant and varied modules of the distribution and specifies the properties of the changes across domains, which serves as prior knowledge of the changing modules for the purpose of deriving the posterior of the target variable $Y$ in the target domain. This provides an end-to-end framework of domain adaptation, in which additional knowledge about how the joint distribution changes, if available, can be directly incorporated to improve the graphical representation. We discuss how causality-based domain adaptation can be put under this umbrella. Experimental results on both synthetic and real data demonstrate the efficacy of the proposed framework for domain adaptation.