Generalized Independent Noise Condition for Estimating Causal Structure with Latent Variables

We investigate the challenging task of learning causal structure in the presence of latent variables, including locating latent variables and determining their quantity, and identifying causal relationships among both latent and observed variables. To address this, we propose a Generalized Independent Noise (GIN) condition for linear non-Gaussian acyclic causal models that incorporate latent variables, which establishes the independence between a linear combination of certain measured variables and some other measured variables. Specifically, for two observed random vectors $\bf{Y}$ and $\bf{Z}$, GIN holds if and only if $\omega^{\intercal}\mathbf{Y}$ and $\mathbf{Z}$ are independent, where $\omega$ is a non-zero parameter vector determined by the cross-covariance between $\mathbf{Y}$ and $\mathbf{Z}$. We then give necessary and sufficient graphical criteria of the GIN condition in linear non-Gaussian acyclic causal models. Roughly speaking, GIN implies the existence of an exogenous set $\mathcal{S}$ relative to the parent set of $\mathbf{Y}$ (w.r.t. the causal ordering), such that $\mathcal{S}$ d-separates $\mathbf{Y}$ from $\mathbf{Z}$. Interestingly, we find that the independent noise condition (i.e., if there is no confounder, causes are independent of the residual derived from regressing the effect on the causes) can be seen as a special case of GIN. With such a connection between GIN and latent causal structures, we further leverage the proposed GIN condition, together with a well-designed search procedure, to efficiently estimate Linear, Non-Gaussian Latent Hierarchical Models (LiNGLaHs), where latent confounders may also be causally related and may even follow a hierarchical structure. We show that the underlying causal structure of a LiNGLaH is identifiable in light of GIN conditions under mild assumptions. Experimental results show the effectiveness of the proposed approach.

Latent Hierarchical Causal Structure Discovery with Rank Constraints

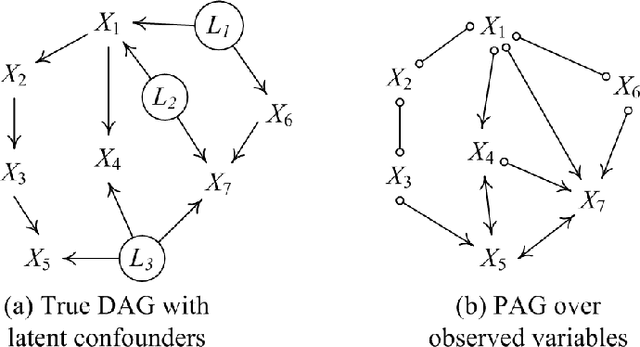
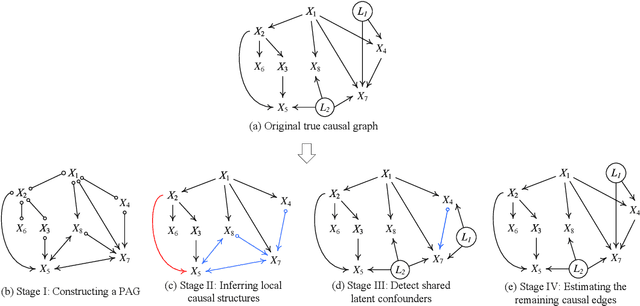
Most causal discovery procedures assume that there are no latent confounders in the system, which is often violated in real-world problems. In this paper, we consider a challenging scenario for causal structure identification, where some variables are latent and they form a hierarchical graph structure to generate the measured variables; the children of latent variables may still be latent and only leaf nodes are measured, and moreover, there can be multiple paths between every pair of variables (i.e., it is beyond tree structure). We propose an estimation procedure that can efficiently locate latent variables, determine their cardinalities, and identify the latent hierarchical structure, by leveraging rank deficiency constraints over the measured variables. We show that the proposed algorithm can find the correct Markov equivalence class of the whole graph asymptotically under proper restrictions on the graph structure.

Action-Sufficient State Representation Learning for Control with Structural Constraints

Perceived signals in real-world scenarios are usually high-dimensional and noisy, and finding and using their representation that contains essential and sufficient information required by downstream decision-making tasks will help improve computational efficiency and generalization ability in the tasks. In this paper, we focus on partially observable environments and propose to learn a minimal set of state representations that capture sufficient information for decision-making, termed \textit{Action-Sufficient state Representations} (ASRs). We build a generative environment model for the structural relationships among variables in the system and present a principled way to characterize ASRs based on structural constraints and the goal of maximizing cumulative reward in policy learning. We then develop a structured sequential Variational Auto-Encoder to estimate the environment model and extract ASRs. Our empirical results on CarRacing and VizDoom demonstrate a clear advantage of learning and using ASRs for policy learning. Moreover, the estimated environment model and ASRs allow learning behaviors from imagined outcomes in the compact latent space to improve sample efficiency.

FRITL: A Hybrid Method for Causal Discovery in the Presence of Latent Confounders

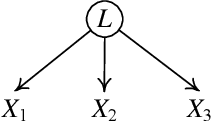
We consider the problem of estimating a particular type of linear non-Gaussian model. Without resorting to the overcomplete Independent Component Analysis (ICA), we show that under some mild assumptions, the model is uniquely identified by a hybrid method. Our method leverages the advantages of constraint-based methods and independent noise-based methods to handle both confounded and unconfounded situations. The first step of our method uses the FCI procedure, which allows confounders and is able to produce asymptotically correct results. The results, unfortunately, usually determine very few unconfounded direct causal relations, because whenever it is possible to have a confounder, it will indicate it. The second step of our procedure finds the unconfounded causal edges between observed variables among only those adjacent pairs informed by the FCI results. By making use of the so-called Triad condition, the third step is able to find confounders and their causal relations with other variables. Afterward, we apply ICA on a notably smaller set of graphs to identify remaining causal relationships if needed. Extensive experiments on simulated data and real-world data validate the correctness and effectiveness of the proposed method.

Generalized Independent Noise Condition for Estimating Linear Non-Gaussian Latent Variable Graphs

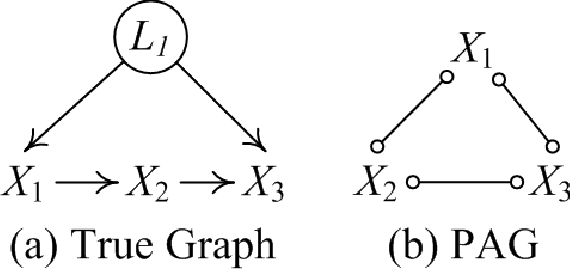
Causal discovery aims to recover causal structures or models underlying the observed data. Despite its success in certain domains, most existing methods focus on causal relations between observed variables, while in many scenarios the observed ones may not be the underlying causal variables (e.g., image pixels), but are generated by latent causal variables or confounders that are causally related. To this end, in this paper, we consider Linear, Non-Gaussian Latent variable Models (LiNGLaMs), in which latent confounders are also causally related, and propose a Generalized Independent Noise (GIN) condition to estimate such latent variable graphs. Specifically, for two observed random vectors $\mathbf{Y}$ and $\mathbf{Z}$, GIN holds if and only if $\omega^{\intercal}\mathbf{Y}$ and $\mathbf{Z}$ are statistically independent, where $\omega$ is a parameter vector characterized from the cross-covariance between $\mathbf{Y}$ and $\mathbf{Z}$. From the graphical view, roughly speaking, GIN implies that causally earlier latent common causes of variables in $\mathbf{Y}$ d-separate $\mathbf{Y}$ from $\mathbf{Z}$. Interestingly, we find that the independent noise condition, i.e., if there is no confounder, causes are independent from the error of regressing the effect on the causes, can be seen as a special case of GIN. Moreover, we show that GIN helps locate latent variables and identify their causal structure, including causal directions. We further develop a recursive learning algorithm to achieve these goals. Experimental results on synthetic and real-world data demonstrate the effectiveness of our method.

Domain Adaptation As a Problem of Inference on Graphical Models

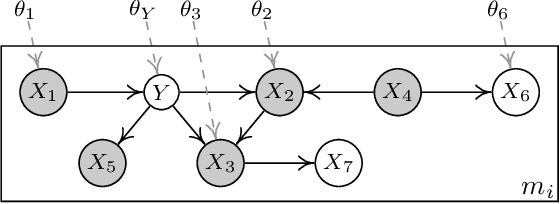
This paper is concerned with data-driven unsupervised domain adaptation, where it is unknown in advance how the joint distribution changes across domains, i.e., what factors or modules of the data distribution remain invariant or change across domains. To develop an automated way of domain adaptation with multiple source domains, we propose to use a graphical model as a compact way to encode the change property of the joint distribution, which can be learned from data, and then view domain adaptation as a problem of Bayesian inference on the graphical models. Such a graphical model distinguishes between constant and varied modules of the distribution and specifies the properties of the changes across domains, which serves as prior knowledge of the changing modules for the purpose of deriving the posterior of the target variable $Y$ in the target domain. This provides an end-to-end framework of domain adaptation, in which additional knowledge about how the joint distribution changes, if available, can be directly incorporated to improve the graphical representation. We discuss how causality-based domain adaptation can be put under this umbrella. Experimental results on both synthetic and real data demonstrate the efficacy of the proposed framework for domain adaptation.

Identification of Effective Connectivity Subregions

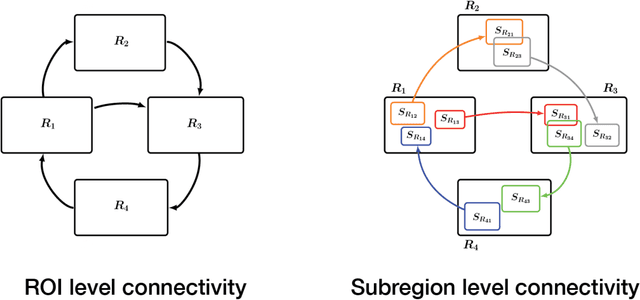
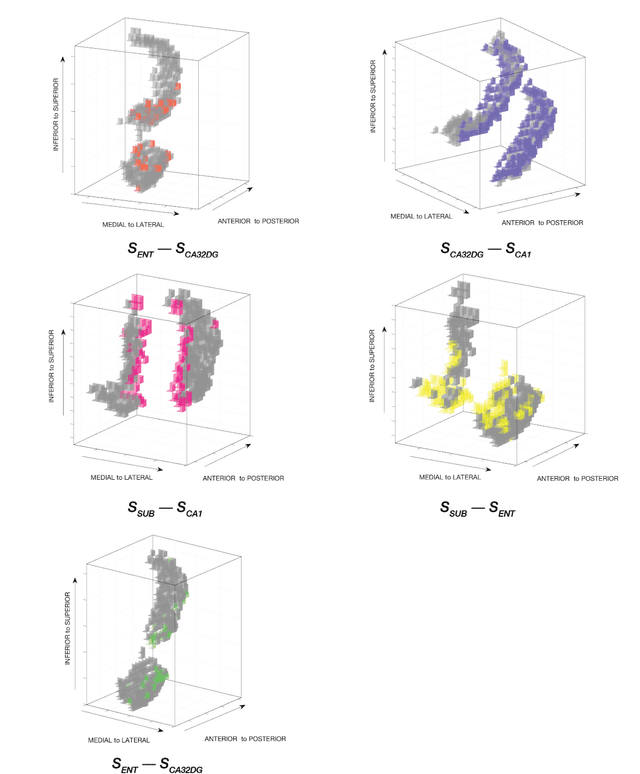
Standard fMRI connectivity analyses depend on aggregating the time series of individual voxels within regions of interest (ROIs). In certain cases, this spatial aggregation implies a loss of valuable functional and anatomical information about smaller subsets of voxels that drive the ROI level connectivity. We use two recently published graphical search methods to identify subsets of voxels that are highly responsible for the connectivity between larger ROIs. To illustrate the procedure, we apply both methods to longitudinal high-resolution resting state fMRI data from regions in the medial temporal lobe from a single individual. Both methods recovered similar subsets of voxels within larger ROIs of entorhinal cortex and hippocampus subfields that also show spatial consistency across different scanning sessions and across hemispheres. In contrast to standard functional connectivity methods, both algorithms applied here are robust against false positive connections produced by common causes and indirect paths (in contrast to Pearson's correlation) and common effect conditioning (in contrast to partial correlation based approaches). These algorithms allow for identification of subregions of voxels driving the connectivity between regions of interest, recovering valuable anatomical and functional information that is lost when ROIs are aggregated. Both methods are specially suited for voxelwise connectivity research, given their running times and scalability to big data problems.

Causal Discovery and Forecasting in Nonstationary Environments with State-Space Models

In many scientific fields, such as economics and neuroscience, we are often faced with nonstationary time series, and concerned with both finding causal relations and forecasting the values of variables of interest, both of which are particularly challenging in such nonstationary environments. In this paper, we study causal discovery and forecasting for nonstationary time series. By exploiting a particular type of state-space model to represent the processes, we show that nonstationarity helps to identify causal structure and that forecasting naturally benefits from learned causal knowledge. Specifically, we allow changes in both causal strengths and noise variances in the nonlinear state-space models, which, interestingly, renders both the causal structure and model parameters identifiable. Given the causal model, we treat forecasting as a problem in Bayesian inference in the causal model, which exploits the time-varying property of the data and adapts to new observations in a principled manner. Experimental results on synthetic and real-world data sets demonstrate the efficacy of the proposed methods.

Causal Discovery from Heterogeneous/Nonstationary Data

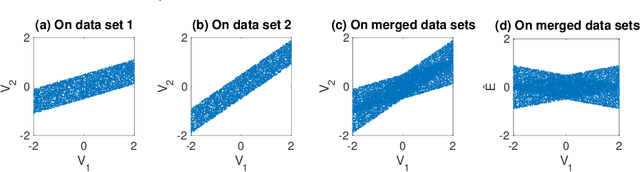
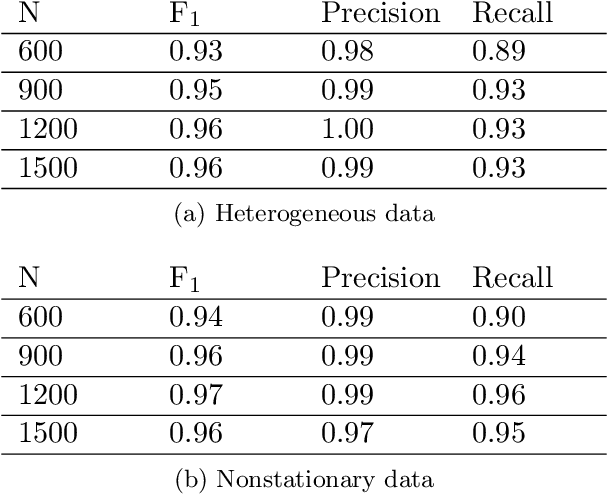
It is commonplace to encounter heterogeneous or nonstationary data, of which the underlying generating process changes across domains or over time. Such a distribution shift feature presents both challenges and opportunities for causal discovery. In this paper, we develop a framework for causal discovery from such data, called Constraint-based causal Discovery from heterogeneous/NOnstationary Data (CD-NOD), to find causal skeleton and directions and estimate the properties of mechanism changes. First, we propose an enhanced constraint-based procedure to detect variables whose local mechanisms change and recover the skeleton of the causal structure over observed variables. Second, we present a method to determine causal orientations by making use of independent changes in the data distribution implied by the underlying causal model, benefiting from information carried by changing distributions. After learning the causal structure, next, we investigate how to efficiently estimate the `driving force' of the nonstationarity of a causal mechanism. That is, we aim to extract from data a low-dimensional representation of changes. The proposed methods are nonparametric, with no hard restrictions on data distributions and causal mechanisms, and do not rely on window segmentation. Furthermore, we find that data heterogeneity benefits causal structure identification even with particular types of confounders. Finally, we show the connection between heterogeneity/nonstationarity and soft intervention in causal discovery. Experimental results on various synthetic and real-world data sets (task-fMRI and stock market data) are presented to demonstrate the efficacy of the proposed methods.

Causal Generative Domain Adaptation Networks

An essential problem in domain adaptation is to understand and make use of distribution changes across domains. For this purpose, we first propose a flexible Generative Domain Adaptation Network (G-DAN) with specific latent variables to capture changes in the generating process of features across domains. By explicitly modeling the changes, one can even generate data in new domains using the generating process with new values for the latent variables in G-DAN. In practice, the process to generate all features together may involve high-dimensional latent variables, requiring dealing with distributions in high dimensions and making it difficult to learn domain changes from few source domains. Interestingly, by further making use of the causal representation of joint distributions, we then decompose the joint distribution into separate modules, each of which involves different low-dimensional latent variables and can be learned separately, leading to a Causal G-DAN (CG-DAN). This improves both statistical and computational efficiency of the learning procedure. Finally, by matching the feature distribution in the target domain, we can recover the target-domain joint distribution and derive the learning machine for the target domain. We demonstrate the efficacy of both G-DAN and CG-DAN in domain generation and cross-domain prediction on both synthetic and real data experiments.