Continually Evolved Multimodal Foundation Models for Cancer Prognosis

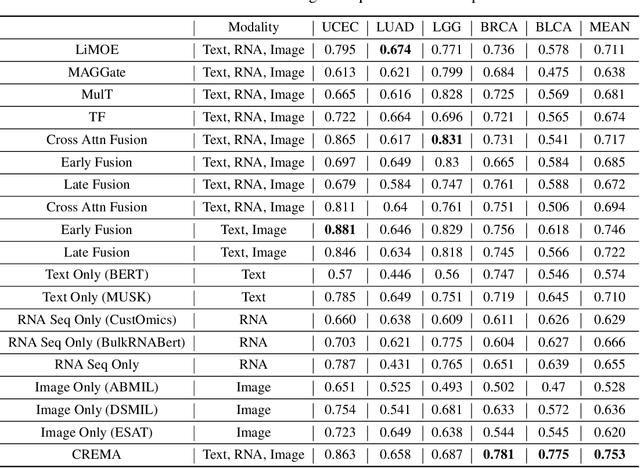
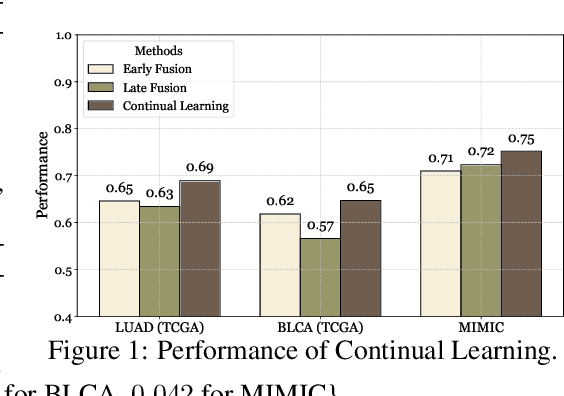
Cancer prognosis is a critical task that involves predicting patient outcomes and survival rates. To enhance prediction accuracy, previous studies have integrated diverse data modalities, such as clinical notes, medical images, and genomic data, leveraging their complementary information. However, existing approaches face two major limitations. First, they struggle to incorporate newly arrived data with varying distributions into training, such as patient records from different hospitals, thus rendering sub-optimal generalizability and limited utility in real-world applications. Second, most multimodal integration methods rely on simplistic concatenation or task-specific pipelines, which fail to capture the complex interdependencies across modalities. To address these, we propose a continually evolving multi-modal foundation model. Extensive experiments on the TCGA dataset demonstrate the effectiveness of our approach, highlighting its potential to advance cancer prognosis by enabling robust and adaptive multimodal integration.

Local Learning for Covariate Selection in Nonparametric Causal Effect Estimation with Latent Variables

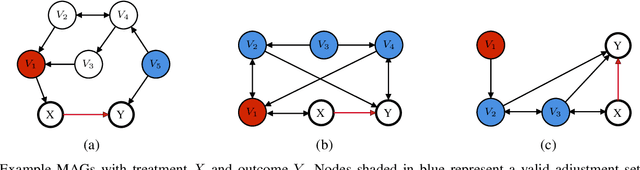
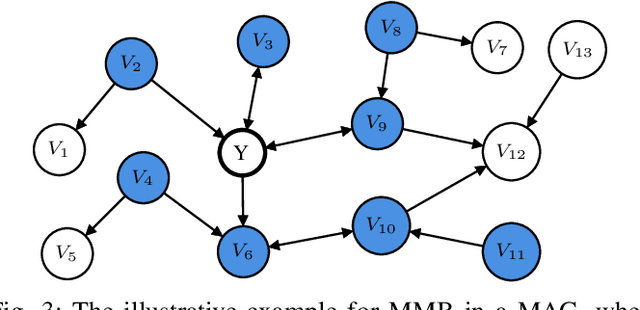
Estimating causal effects from nonexperimental data is a fundamental problem in many fields of science. A key component of this task is selecting an appropriate set of covariates for confounding adjustment to avoid bias. Most existing methods for covariate selection often assume the absence of latent variables and rely on learning the global network structure among variables. However, identifying the global structure can be unnecessary and inefficient, especially when our primary interest lies in estimating the effect of a treatment variable on an outcome variable. To address this limitation, we propose a novel local learning approach for covariate selection in nonparametric causal effect estimation, which accounts for the presence of latent variables. Our approach leverages testable independence and dependence relationships among observed variables to identify a valid adjustment set for a target causal relationship, ensuring both soundness and completeness under standard assumptions. We validate the effectiveness of our algorithm through extensive experiments on both synthetic and real-world data.

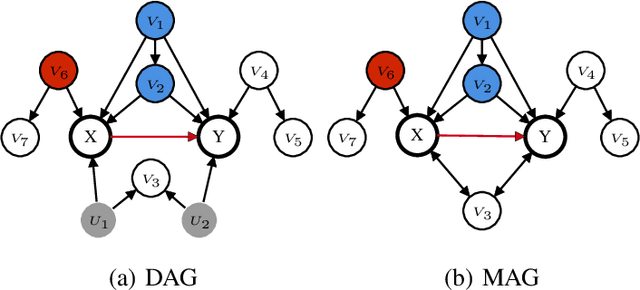
Testability of Instrumental Variables in Additive Nonlinear, Non-Constant Effects Models

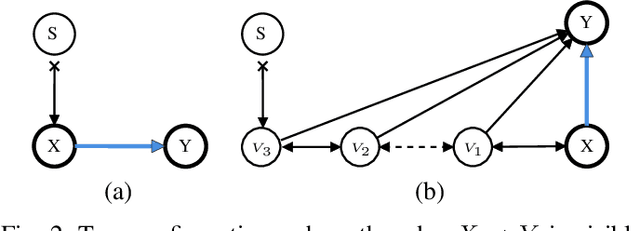
We address the issue of the testability of instrumental variables derived from observational data. Most existing testable implications are centered on scenarios where the treatment is a discrete variable, e.g., instrumental inequality (Pearl, 1995), or where the effect is assumed to be constant, e.g., instrumental variables condition based on the principle of independent mechanisms (Burauel, 2023). However, treatments can often be continuous variables, such as drug dosages or nutritional content levels, and non-constant effects may occur in many real-world scenarios. In this paper, we consider an additive nonlinear, non-constant effects model with unmeasured confounders, in which treatments can be either discrete or continuous, and propose an Auxiliary-based Independence Test (AIT) condition to test whether a variable is a valid instrument. We first show that if the candidate instrument is valid, then the AIT condition holds. Moreover, we illustrate the implications of the AIT condition and demonstrate that, in certain conditions, AIT conditions are necessary and sufficient to detect all invalid IVs. We also extend the AIT condition to include covariates and introduce a practical testing algorithm. Experimental results on both synthetic and three different real-world datasets show the effectiveness of our proposed condition.

Learning to Move Like Professional Counter-Strike Players

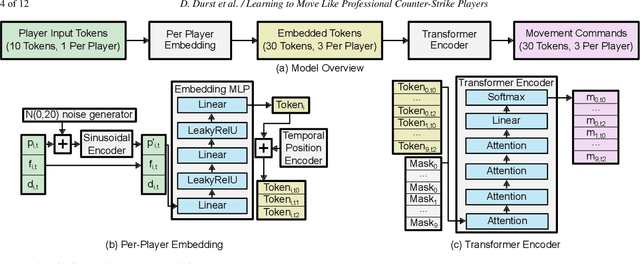
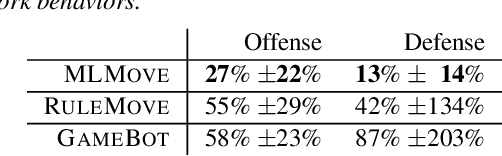
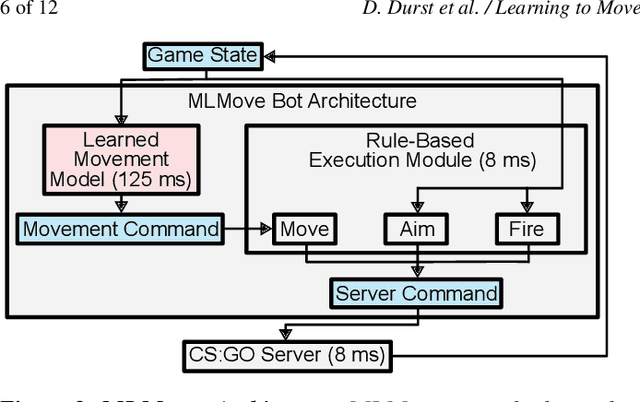
In multiplayer, first-person shooter games like Counter-Strike: Global Offensive (CS:GO), coordinated movement is a critical component of high-level strategic play. However, the complexity of team coordination and the variety of conditions present in popular game maps make it impractical to author hand-crafted movement policies for every scenario. We show that it is possible to take a data-driven approach to creating human-like movement controllers for CS:GO. We curate a team movement dataset comprising 123 hours of professional game play traces, and use this dataset to train a transformer-based movement model that generates human-like team movement for all players in a "Retakes" round of the game. Importantly, the movement prediction model is efficient. Performing inference for all players takes less than 0.5 ms per game step (amortized cost) on a single CPU core, making it plausible for use in commercial games today. Human evaluators assess that our model behaves more like humans than both commercially-available bots and procedural movement controllers scripted by experts (16% to 59% higher by TrueSkill rating of "human-like"). Using experiments involving in-game bot vs. bot self-play, we demonstrate that our model performs simple forms of teamwork, makes fewer common movement mistakes, and yields movement distributions, player lifetimes, and kill locations similar to those observed in professional CS:GO match play.

Identification and Estimation of the Bi-Directional MR with Some Invalid Instruments

We consider the challenging problem of estimating causal effects from purely observational data in the bi-directional Mendelian randomization (MR), where some invalid instruments, as well as unmeasured confounding, usually exist. To address this problem, most existing methods attempt to find proper valid instrumental variables (IVs) for the target causal effect by expert knowledge or by assuming that the causal model is a one-directional MR model. As such, in this paper, we first theoretically investigate the identification of the bi-directional MR from observational data. In particular, we provide necessary and sufficient conditions under which valid IV sets are correctly identified such that the bi-directional MR model is identifiable, including the causal directions of a pair of phenotypes (i.e., the treatment and outcome). Moreover, based on the identification theory, we develop a cluster fusion-like method to discover valid IV sets and estimate the causal effects of interest. We theoretically demonstrate the correctness of the proposed algorithm. Experimental results show the effectiveness of our method for estimating causal effects in bi-directional MR.

Learning Discrete Latent Variable Structures with Tensor Rank Conditions

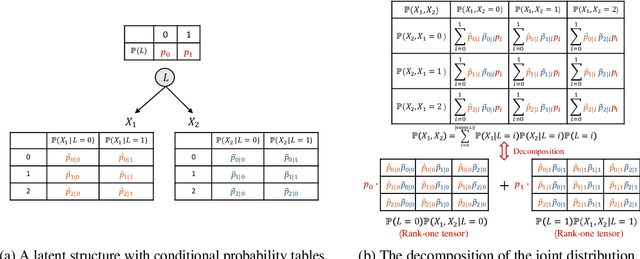
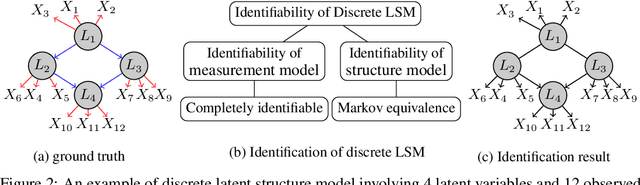
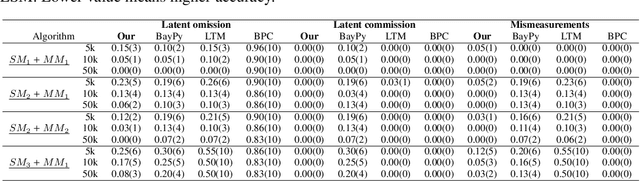
Unobserved discrete data are ubiquitous in many scientific disciplines, and how to learn the causal structure of these latent variables is crucial for uncovering data patterns. Most studies focus on the linear latent variable model or impose strict constraints on latent structures, which fail to address cases in discrete data involving non-linear relationships or complex latent structures. To achieve this, we explore a tensor rank condition on contingency tables for an observed variable set $\mathbf{X}_p$, showing that the rank is determined by the minimum support of a specific conditional set (not necessary in $\mathbf{X}_p$) that d-separates all variables in $\mathbf{X}_p$. By this, one can locate the latent variable through probing the rank on different observed variables set, and further identify the latent causal structure under some structure assumptions. We present the corresponding identification algorithm and conduct simulated experiments to verify the effectiveness of our method. In general, our results elegantly extend the identification boundary for causal discovery with discrete latent variables and expand the application scope of causal discovery with latent variables.

Local Causal Structure Learning in the Presence of Latent Variables

Discovering causal relationships from observational data, particularly in the presence of latent variables, poses a challenging problem. While current local structure learning methods have proven effective and efficient when the focus lies solely on the local relationships of a target variable, they operate under the assumption of causal sufficiency. This assumption implies that all the common causes of the measured variables are observed, leaving no room for latent variables. Such a premise can be easily violated in various real-world applications, resulting in inaccurate structures that may adversely impact downstream tasks. In light of this, our paper delves into the primary investigation of locally identifying potential parents and children of a target from observational data that may include latent variables. Specifically, we harness the causal information from m-separation and V-structures to derive theoretical consistency results, effectively bridging the gap between global and local structure learning. Together with the newly developed stop rules, we present a principled method for determining whether a variable is a direct cause or effect of a target. Further, we theoretically demonstrate the correctness of our approach under the standard causal Markov and faithfulness conditions, with infinite samples. Experimental results on both synthetic and real-world data validate the effectiveness and efficiency of our approach.

Automating the Selection of Proxy Variables of Unmeasured Confounders

Recently, interest has grown in the use of proxy variables of unobserved confounding for inferring the causal effect in the presence of unmeasured confounders from observational data. One difficulty inhibiting the practical use is finding valid proxy variables of unobserved confounding to a target causal effect of interest. These proxy variables are typically justified by background knowledge. In this paper, we investigate the estimation of causal effects among multiple treatments and a single outcome, all of which are affected by unmeasured confounders, within a linear causal model, without prior knowledge of the validity of proxy variables. To be more specific, we first extend the existing proxy variable estimator, originally addressing a single unmeasured confounder, to accommodate scenarios where multiple unmeasured confounders exist between the treatments and the outcome. Subsequently, we present two different sets of precise identifiability conditions for selecting valid proxy variables of unmeasured confounders, based on the second-order statistics and higher-order statistics of the data, respectively. Moreover, we propose two data-driven methods for the selection of proxy variables and for the unbiased estimation of causal effects. Theoretical analysis demonstrates the correctness of our proposed algorithms. Experimental results on both synthetic and real-world data show the effectiveness of the proposed approach.

Policy Learning for Balancing Short-Term and Long-Term Rewards

Empirical researchers and decision-makers spanning various domains frequently seek profound insights into the long-term impacts of interventions. While the significance of long-term outcomes is undeniable, an overemphasis on them may inadvertently overshadow short-term gains. Motivated by this, this paper formalizes a new framework for learning the optimal policy that effectively balances both long-term and short-term rewards, where some long-term outcomes are allowed to be missing. In particular, we first present the identifiability of both rewards under mild assumptions. Next, we deduce the semiparametric efficiency bounds, along with the consistency and asymptotic normality of their estimators. We also reveal that short-term outcomes, if associated, contribute to improving the estimator of the long-term reward. Based on the proposed estimators, we develop a principled policy learning approach and further derive the convergence rates of regret and estimation errors associated with the learned policy. Extensive experiments are conducted to validate the effectiveness of the proposed method, demonstrating its practical applicability.

Survival modeling using deep learning, machine learning and statistical methods: A comparative analysis for predicting mortality after hospital admission

Survival analysis is essential for studying time-to-event outcomes and providing a dynamic understanding of the probability of an event occurring over time. Various survival analysis techniques, from traditional statistical models to state-of-the-art machine learning algorithms, support healthcare intervention and policy decisions. However, there remains ongoing discussion about their comparative performance. We conducted a comparative study of several survival analysis methods, including Cox proportional hazards (CoxPH), stepwise CoxPH, elastic net penalized Cox model, Random Survival Forests (RSF), Gradient Boosting machine (GBM) learning, AutoScore-Survival, DeepSurv, time-dependent Cox model based on neural network (CoxTime), and DeepHit survival neural network. We applied the concordance index (C-index) for model goodness-of-fit, and integral Brier scores (IBS) for calibration, and considered the model interpretability. As a case study, we performed a retrospective analysis of patients admitted through the emergency department of a tertiary hospital from 2017 to 2019, predicting 90-day all-cause mortality based on patient demographics, clinicopathological features, and historical data. The results of the C-index indicate that deep learning achieved comparable performance, with DeepSurv producing the best discrimination (DeepSurv: 0.893; CoxTime: 0.892; DeepHit: 0.891). The calibration of DeepSurv (IBS: 0.041) performed the best, followed by RSF (IBS: 0.042) and GBM (IBS: 0.0421), all using the full variables. Moreover, AutoScore-Survival, using a minimal variable subset, is easy to interpret, and can achieve good discrimination and calibration (C-index: 0.867; IBS: 0.044). While all models were satisfactory, DeepSurv exhibited the best discrimination and calibration. In addition, AutoScore-Survival offers a more parsimonious model and excellent interpretability.