Should Bias Always be Eliminated? A Principled Framework to Use Data Bias for OOD Generation

Most existing methods for adapting models to out-of-distribution (OOD) domains rely on invariant representation learning to eliminate the influence of biased features. However, should bias always be eliminated -- and if not, when should it be retained, and how can it be leveraged? To address these questions, we first present a theoretical analysis that explores the conditions under which biased features can be identified and effectively utilized. Building on this theoretical foundation, we introduce a novel framework that strategically leverages bias to complement invariant representations during inference. The framework comprises two key components that leverage bias in both direct and indirect ways: (1) using invariance as guidance to extract predictive ingredients from bias, and (2) exploiting identified bias to estimate the environmental condition and then use it to explore appropriate bias-aware predictors to alleviate environment gaps. We validate our approach through experiments on both synthetic datasets and standard domain generalization benchmarks. Results consistently demonstrate that our method outperforms existing approaches, underscoring its robustness and adaptability.

Sequential Treatment Effect Estimation with Unmeasured Confounders

This paper studies the cumulative causal effects of sequential treatments in the presence of unmeasured confounders. It is a critical issue in sequential decision-making scenarios where treatment decisions and outcomes dynamically evolve over time. Advanced causal methods apply transformer as a backbone to model such time sequences, which shows superiority in capturing long time dependence and periodic patterns via attention mechanism. However, even they control the observed confounding, these estimators still suffer from unmeasured confounders, which influence both treatment assignments and outcomes. How to adjust the latent confounding bias in sequential treatment effect estimation remains an open challenge. Therefore, we propose a novel Decomposing Sequential Instrumental Variable framework for CounterFactual Regression (DSIV-CFR), relying on a common negative control assumption. Specifically, an instrumental variable (IV) is a special negative control exposure, while the previous outcome serves as a negative control outcome. This allows us to recover the IVs latent in observation variables and estimate sequential treatment effects via a generalized moment condition. We conducted experiments on 4 datasets and achieved significant performance in one- and multi-step prediction, supported by which we can identify optimal treatments for dynamic systems.

General Information Metrics for Improving AI Model Training Efficiency

To address the growing size of AI model training data and the lack of a universal data selection methodology-factors that significantly drive up training costs -- this paper presents the General Information Metrics Evaluation (GIME) method. GIME leverages general information metrics from Objective Information Theory (OIT), including volume, delay, scope, granularity, variety, duration, sampling rate, aggregation, coverage, distortion, and mismatch to optimize dataset selection for training purposes. Comprehensive experiments conducted across diverse domains, such as CTR Prediction, Civil Case Prediction, and Weather Forecasting, demonstrate that GIME effectively preserves model performance while substantially reducing both training time and costs. Additionally, applying GIME within the Judicial AI Program led to a remarkable 39.56% reduction in total model training expenses, underscoring its potential to support efficient and sustainable AI development.

Causality for Large Language Models

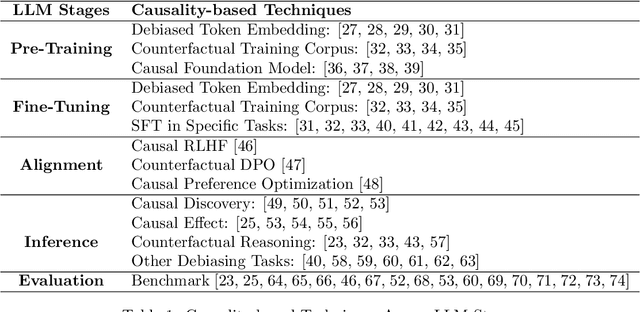
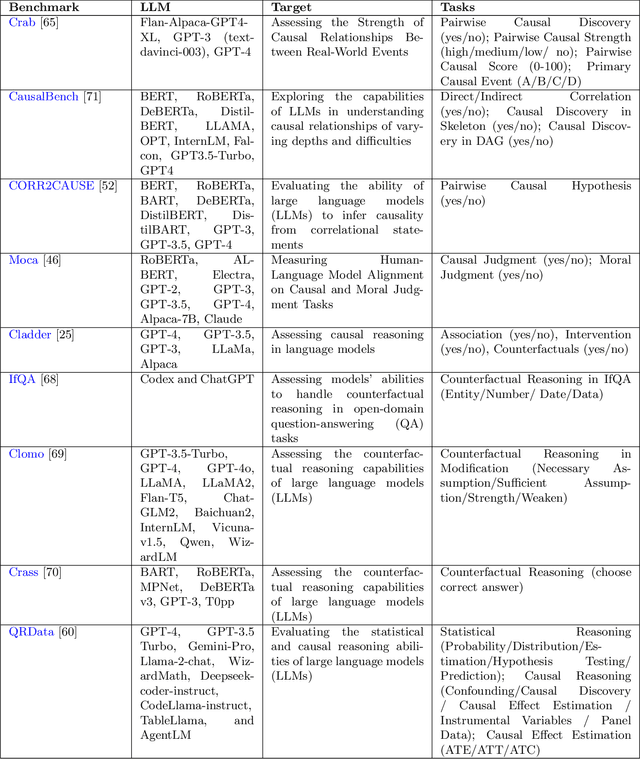
Recent breakthroughs in artificial intelligence have driven a paradigm shift, where large language models (LLMs) with billions or trillions of parameters are trained on vast datasets, achieving unprecedented success across a series of language tasks. However, despite these successes, LLMs still rely on probabilistic modeling, which often captures spurious correlations rooted in linguistic patterns and social stereotypes, rather than the true causal relationships between entities and events. This limitation renders LLMs vulnerable to issues such as demographic biases, social stereotypes, and LLM hallucinations. These challenges highlight the urgent need to integrate causality into LLMs, moving beyond correlation-driven paradigms to build more reliable and ethically aligned AI systems. While many existing surveys and studies focus on utilizing prompt engineering to activate LLMs for causal knowledge or developing benchmarks to assess their causal reasoning abilities, most of these efforts rely on human intervention to activate pre-trained models. How to embed causality into the training process of LLMs and build more general and intelligent models remains unexplored. Recent research highlights that LLMs function as causal parrots, capable of reciting causal knowledge without truly understanding or applying it. These prompt-based methods are still limited to human interventional improvements. This survey aims to address this gap by exploring how causality can enhance LLMs at every stage of their lifecycle-from token embedding learning and foundation model training to fine-tuning, alignment, inference, and evaluation-paving the way for more interpretable, reliable, and causally-informed models. Additionally, we further outline six promising future directions to advance LLM development, enhance their causal reasoning capabilities, and address the current limitations these models face.

Generalized Encouragement-Based Instrumental Variables for Counterfactual Regression

In causal inference, encouragement designs (EDs) are widely used to analyze causal effects, when randomized controlled trials (RCTs) are impractical or compliance to treatment cannot be perfectly enforced. Unlike RCTs, which directly allocate treatments, EDs randomly assign encouragement policies that positively motivate individuals to engage in a specific treatment. These random encouragements act as instrumental variables (IVs), facilitating the identification of causal effects through leveraging exogenous perturbations in discrete treatment scenarios. However, real-world applications of encouragement designs often face challenges such as incomplete randomization, limited experimental data, and significantly fewer encouragements compared to treatments, hindering precise causal effect estimation. To address this, this paper introduces novel theories and algorithms for identifying the Conditional Average Treatment Effect (CATE) using variations in encouragement. Further, by leveraging both observational and encouragement data, we propose a generalized IV estimator, named Encouragement-based Counterfactual Regression (EnCounteR), to effectively estimate the causal effects. Extensive experiments on both synthetic and real-world datasets demonstrate the superiority of EnCounteR over existing methods.

Causal Inference with Complex Treatments: A Survey

Causal inference plays an important role in explanatory analysis and decision making across various fields like statistics, marketing, health care, and education. Its main task is to estimate treatment effects and make intervention policies. Traditionally, most of the previous works typically focus on the binary treatment setting that there is only one treatment for a unit to adopt or not. However, in practice, the treatment can be much more complex, encompassing multi-valued, continuous, or bundle options. In this paper, we refer to these as complex treatments and systematically and comprehensively review the causal inference methods for addressing them. First, we formally revisit the problem definition, the basic assumptions, and their possible variations under specific conditions. Second, we sequentially review the related methods for multi-valued, continuous, and bundled treatment settings. In each situation, we tentatively divide the methods into two categories: those conforming to the unconfoundedness assumption and those violating it. Subsequently, we discuss the available datasets and open-source codes. Finally, we provide a brief summary of these works and suggest potential directions for future research.

Stable Heterogeneous Treatment Effect Estimation across Out-of-Distribution Populations

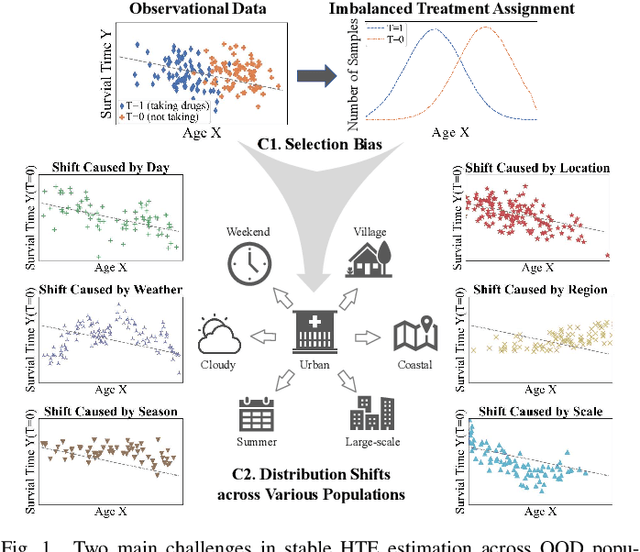
Heterogeneous treatment effect (HTE) estimation is vital for understanding the change of treatment effect across individuals or subgroups. Most existing HTE estimation methods focus on addressing selection bias induced by imbalanced distributions of confounders between treated and control units, but ignore distribution shifts across populations. Thereby, their applicability has been limited to the in-distribution (ID) population, which shares a similar distribution with the training dataset. In real-world applications, where population distributions are subject to continuous changes, there is an urgent need for stable HTE estimation across out-of-distribution (OOD) populations, which, however, remains an open problem. As pioneers in resolving this problem, we propose a novel Stable Balanced Representation Learning with Hierarchical-Attention Paradigm (SBRL-HAP) framework, which consists of 1) Balancing Regularizer for eliminating selection bias, 2) Independence Regularizer for addressing the distribution shift issue, 3) Hierarchical-Attention Paradigm for coordination between balance and independence. In this way, SBRL-HAP regresses counterfactual outcomes using ID data, while ensuring the resulting HTE estimation can be successfully generalized to out-of-distribution scenarios, thereby enhancing the model's applicability in real-world settings. Extensive experiments conducted on synthetic and real-world datasets demonstrate the effectiveness of our SBRL-HAP in achieving stable HTE estimation across OOD populations, with an average 10% reduction in the error metric PEHE and 11% decrease in the ATE bias, compared to the SOTA methods.

Learning Discrete Latent Variable Structures with Tensor Rank Conditions

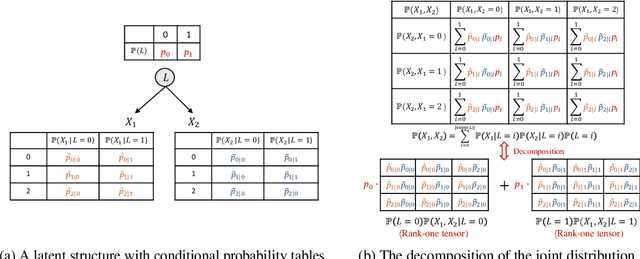
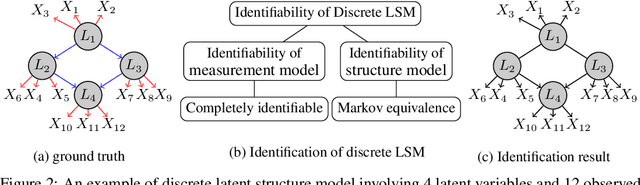
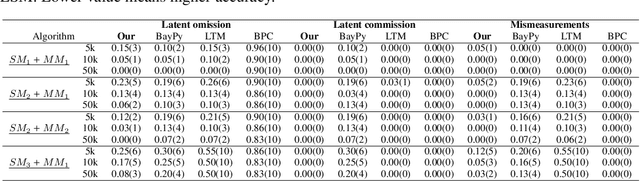
Unobserved discrete data are ubiquitous in many scientific disciplines, and how to learn the causal structure of these latent variables is crucial for uncovering data patterns. Most studies focus on the linear latent variable model or impose strict constraints on latent structures, which fail to address cases in discrete data involving non-linear relationships or complex latent structures. To achieve this, we explore a tensor rank condition on contingency tables for an observed variable set $\mathbf{X}_p$, showing that the rank is determined by the minimum support of a specific conditional set (not necessary in $\mathbf{X}_p$) that d-separates all variables in $\mathbf{X}_p$. By this, one can locate the latent variable through probing the rank on different observed variables set, and further identify the latent causal structure under some structure assumptions. We present the corresponding identification algorithm and conduct simulated experiments to verify the effectiveness of our method. In general, our results elegantly extend the identification boundary for causal discovery with discrete latent variables and expand the application scope of causal discovery with latent variables.

Contrastive Balancing Representation Learning for Heterogeneous Dose-Response Curves Estimation

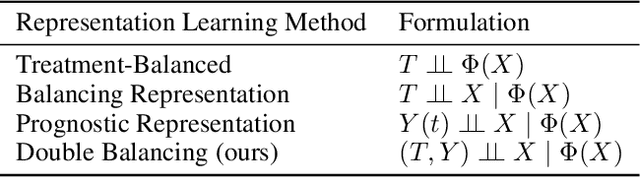
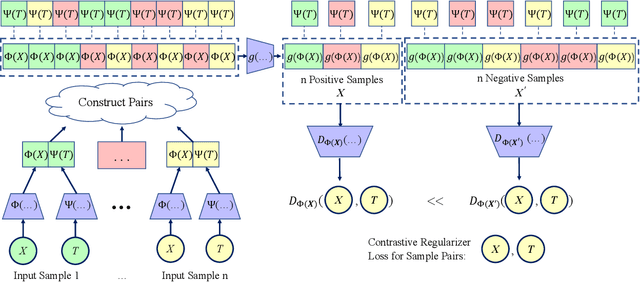
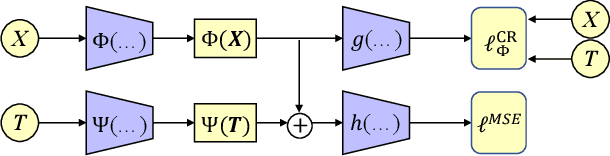
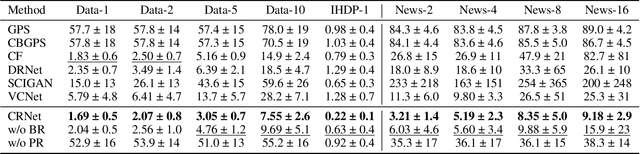
Estimating the individuals' potential response to varying treatment doses is crucial for decision-making in areas such as precision medicine and management science. Most recent studies predict counterfactual outcomes by learning a covariate representation that is independent of the treatment variable. However, such independence constraints neglect much of the covariate information that is useful for counterfactual prediction, especially when the treatment variables are continuous. To tackle the above issue, in this paper, we first theoretically demonstrate the importance of the balancing and prognostic representations for unbiased estimation of the heterogeneous dose-response curves, that is, the learned representations are constrained to satisfy the conditional independence between the covariates and both of the treatment variables and the potential responses. Based on this, we propose a novel Contrastive balancing Representation learning Network using a partial distance measure, called CRNet, for estimating the heterogeneous dose-response curves without losing the continuity of treatments. Extensive experiments are conducted on synthetic and real-world datasets demonstrating that our proposal significantly outperforms previous methods.

Pareto-Optimal Estimation and Policy Learning on Short-term and Long-term Treatment Effects

This paper focuses on developing Pareto-optimal estimation and policy learning to identify the most effective treatment that maximizes the total reward from both short-term and long-term effects, which might conflict with each other. For example, a higher dosage of medication might increase the speed of a patient's recovery (short-term) but could also result in severe long-term side effects. Although recent works have investigated the problems about short-term or long-term effects or the both, how to trade-off between them to achieve optimal treatment remains an open challenge. Moreover, when multiple objectives are directly estimated using conventional causal representation learning, the optimization directions among various tasks can conflict as well. In this paper, we systematically investigate these issues and introduce a Pareto-Efficient algorithm, comprising Pareto-Optimal Estimation (POE) and Pareto-Optimal Policy Learning (POPL), to tackle them. POE incorporates a continuous Pareto module with representation balancing, enhancing estimation efficiency across multiple tasks. As for POPL, it involves deriving short-term and long-term outcomes linked with various treatment levels, facilitating an exploration of the Pareto frontier emanating from these outcomes. Results on both the synthetic and real-world datasets demonstrate the superiority of our method.