Long-Term Individual Causal Effect Estimation via Identifiable Latent Representation Learning

Estimating long-term causal effects by combining long-term observational and short-term experimental data is a crucial but challenging problem in many real-world scenarios. In existing methods, several ideal assumptions, e.g. latent unconfoundedness assumption or additive equi-confounding bias assumption, are proposed to address the latent confounder problem raised by the observational data. However, in real-world applications, these assumptions are typically violated which limits their practical effectiveness. In this paper, we tackle the problem of estimating the long-term individual causal effects without the aforementioned assumptions. Specifically, we propose to utilize the natural heterogeneity of data, such as data from multiple sources, to identify latent confounders, thereby significantly avoiding reliance on idealized assumptions. Practically, we devise a latent representation learning-based estimator of long-term causal effects. Theoretically, we establish the identifiability of latent confounders, with which we further achieve long-term effect identification. Extensive experimental studies, conducted on multiple synthetic and semi-synthetic datasets, demonstrate the effectiveness of our proposed method.

Treatment Effect Estimation for Exponential Family Outcomes using Neural Networks with Targeted Regularization

Neural Networks (NNs) have became a natural choice for treatment effect estimation due to their strong approximation capabilities. Nevertheless, how to design NN-based estimators with desirable properties, such as low bias and doubly robustness, still remains a significant challenge. A common approach to address this is targeted regularization, which modifies the objective function of NNs. However, existing works on targeted regularization are limited to Gaussian-distributed outcomes, significantly restricting their applicability in real-world scenarios. In this work, we aim to bridge this blank by extending this framework to the boarder exponential family outcomes. Specifically, we first derive the von-Mises expansion of the Average Dose function of Canonical Functions (ADCF), which inspires us how to construct a doubly robust estimator with good properties. Based on this, we develop a NN-based estimator for ADCF by generalizing functional targeted regularization to exponential families, and provide the corresponding theoretical convergence rate. Extensive experimental results demonstrate the effectiveness of our proposed model.

DFF: Decision-Focused Fine-tuning for Smarter Predict-then-Optimize with Limited Data

Decision-focused learning (DFL) offers an end-to-end approach to the predict-then-optimize (PO) framework by training predictive models directly on decision loss (DL), enhancing decision-making performance within PO contexts. However, the implementation of DFL poses distinct challenges. Primarily, DL can result in deviation from the physical significance of the predictions under limited data. Additionally, some predictive models are non-differentiable or black-box, which cannot be adjusted using gradient-based methods. To tackle the above challenges, we propose a novel framework, Decision-Focused Fine-tuning (DFF), which embeds the DFL module into the PO pipeline via a novel bias correction module. DFF is formulated as a constrained optimization problem that maintains the proximity of the DL-enhanced model to the original predictive model within a defined trust region. We theoretically prove that DFF strictly confines prediction bias within a predetermined upper bound, even with limited datasets, thereby substantially reducing prediction shifts caused by DL under limited data. Furthermore, the bias correction module can be integrated into diverse predictive models, enhancing adaptability to a broad range of PO tasks. Extensive evaluations on synthetic and real-world datasets, including network flow, portfolio optimization, and resource allocation problems with different predictive models, demonstrate that DFF not only improves decision performance but also adheres to fine-tuning constraints, showcasing robust adaptability across various scenarios.

Contrastive Balancing Representation Learning for Heterogeneous Dose-Response Curves Estimation

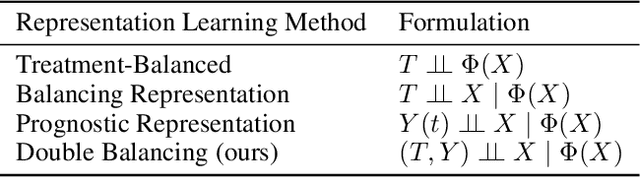
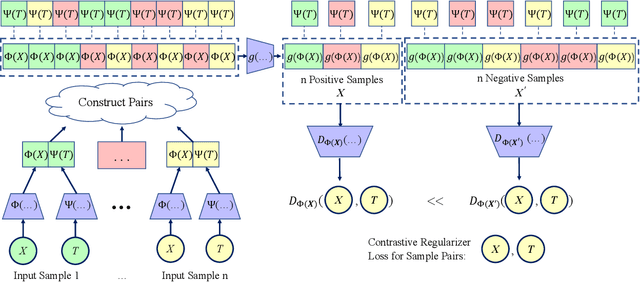
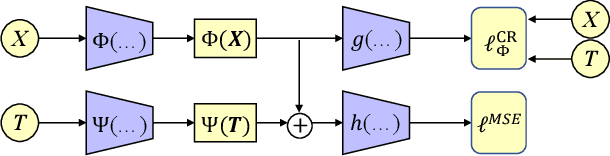
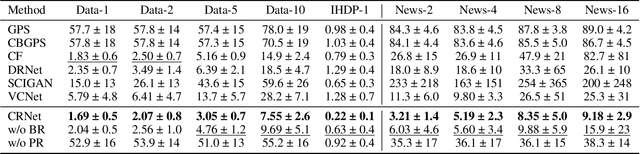
Estimating the individuals' potential response to varying treatment doses is crucial for decision-making in areas such as precision medicine and management science. Most recent studies predict counterfactual outcomes by learning a covariate representation that is independent of the treatment variable. However, such independence constraints neglect much of the covariate information that is useful for counterfactual prediction, especially when the treatment variables are continuous. To tackle the above issue, in this paper, we first theoretically demonstrate the importance of the balancing and prognostic representations for unbiased estimation of the heterogeneous dose-response curves, that is, the learned representations are constrained to satisfy the conditional independence between the covariates and both of the treatment variables and the potential responses. Based on this, we propose a novel Contrastive balancing Representation learning Network using a partial distance measure, called CRNet, for estimating the heterogeneous dose-response curves without losing the continuity of treatments. Extensive experiments are conducted on synthetic and real-world datasets demonstrating that our proposal significantly outperforms previous methods.