Weilin Chen
Long-Term Individual Causal Effect Estimation via Identifiable Latent Representation Learning
May 08, 2025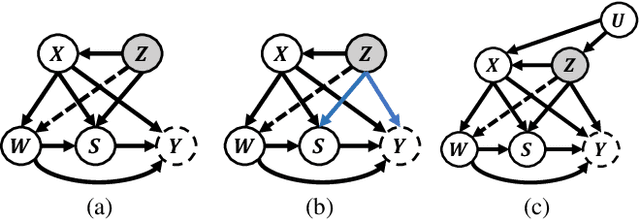
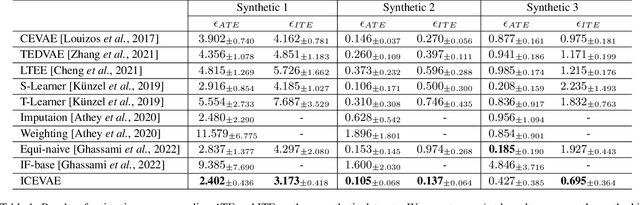
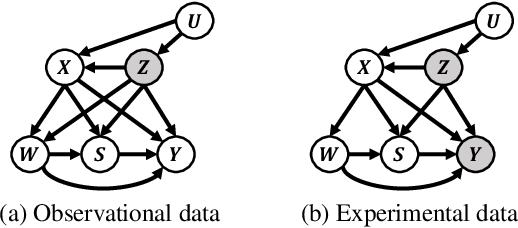
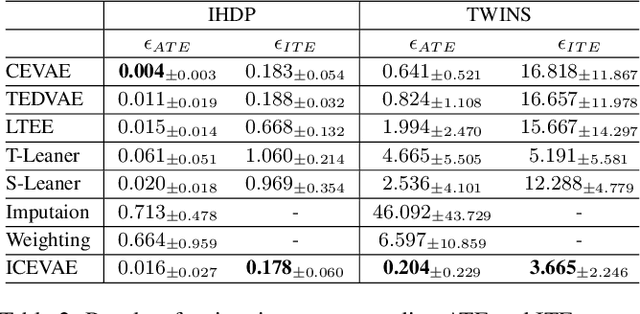
Abstract:Estimating long-term causal effects by combining long-term observational and short-term experimental data is a crucial but challenging problem in many real-world scenarios. In existing methods, several ideal assumptions, e.g. latent unconfoundedness assumption or additive equi-confounding bias assumption, are proposed to address the latent confounder problem raised by the observational data. However, in real-world applications, these assumptions are typically violated which limits their practical effectiveness. In this paper, we tackle the problem of estimating the long-term individual causal effects without the aforementioned assumptions. Specifically, we propose to utilize the natural heterogeneity of data, such as data from multiple sources, to identify latent confounders, thereby significantly avoiding reliance on idealized assumptions. Practically, we devise a latent representation learning-based estimator of long-term causal effects. Theoretically, we establish the identifiability of latent confounders, with which we further achieve long-term effect identification. Extensive experimental studies, conducted on multiple synthetic and semi-synthetic datasets, demonstrate the effectiveness of our proposed method.
Causal Effect Estimation under Networked Interference without Networked Unconfoundedness Assumption
Feb 27, 2025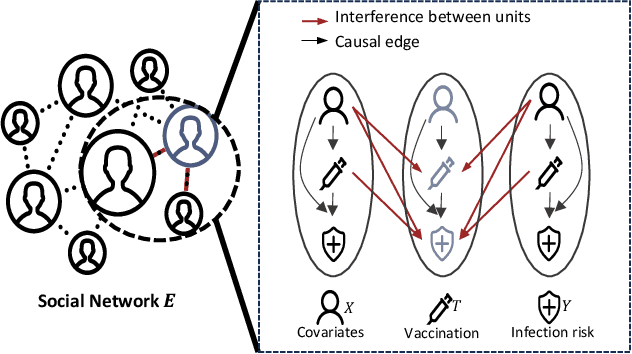
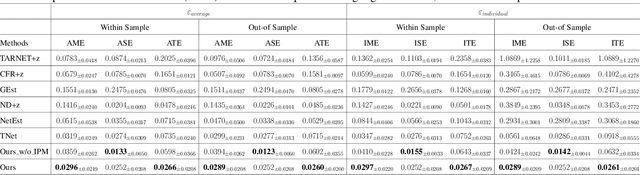
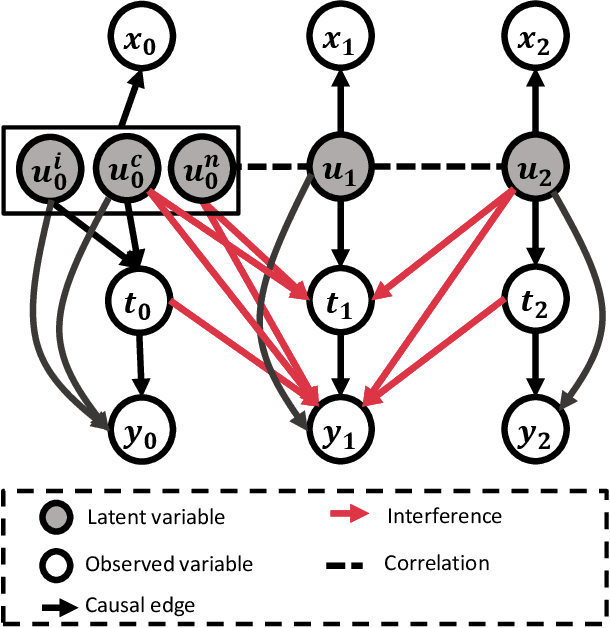
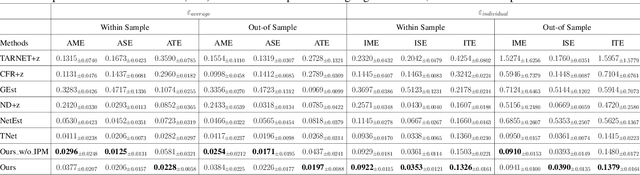
Abstract:Estimating causal effects under networked interference is a crucial yet challenging problem. Existing methods based on observational data mainly rely on the networked unconfoundedness assumption, which guarantees the identification of networked effects. However, the networked unconfoundedness assumption is usually violated due to the latent confounders in observational data, hindering the identification of networked effects. Interestingly, in such networked settings, interactions between units provide valuable information for recovering latent confounders. In this paper, we identify three types of latent confounders in networked inference that hinder identification: those affecting only the individual, those affecting only neighbors, and those influencing both. Specifically, we devise a networked effect estimator based on identifiable representation learning techniques. Theoretically, we establish the identifiability of all latent confounders, and leveraging the identified latent confounders, we provide the networked effect identification result. Extensive experiments validate our theoretical results and demonstrate the effectiveness of the proposed method.
Nonparametric Heterogeneous Long-term Causal Effect Estimation via Data Combination
Feb 26, 2025Abstract:Long-term causal inference has drawn increasing attention in many scientific domains. Existing methods mainly focus on estimating average long-term causal effects by combining long-term observational data and short-term experimental data. However, it is still understudied how to robustly and effectively estimate heterogeneous long-term causal effects, significantly limiting practical applications. In this paper, we propose several two-stage style nonparametric estimators for heterogeneous long-term causal effect estimation, including propensity-based, regression-based, and multiple robust estimators. We conduct a comprehensive theoretical analysis of their asymptotic properties under mild assumptions, with the ultimate goal of building a better understanding of the conditions under which some estimators can be expected to perform better. Extensive experiments across several semi-synthetic and real-world datasets validate the theoretical results and demonstrate the effectiveness of the proposed estimators.
Long-term Causal Inference via Modeling Sequential Latent Confounding
Feb 26, 2025Abstract:Long-term causal inference is an important but challenging problem across various scientific domains. To solve the latent confounding problem in long-term observational studies, existing methods leverage short-term experimental data. Ghassami et al. propose an approach based on the Conditional Additive Equi-Confounding Bias (CAECB) assumption, which asserts that the confounding bias in the short-term outcome is equal to that in the long-term outcome, so that the long-term confounding bias and the causal effects can be identified. While effective in certain cases, this assumption is limited to scenarios with a one-dimensional short-term outcome. In this paper, we introduce a novel assumption that extends the CAECB assumption to accommodate temporal short-term outcomes. Our proposed assumption states a functional relationship between sequential confounding biases across temporal short-term outcomes, under which we theoretically establish the identification of long-term causal effects. Based on the identification result, we develop an estimator and conduct a theoretical analysis of its asymptotic properties. Extensive experiments validate our theoretical results and demonstrate the effectiveness of the proposed method.
Estimating Long-term Heterogeneous Dose-response Curve: Generalization Bound Leveraging Optimal Transport Weights
Jun 27, 2024



Abstract:Long-term causal effect estimation is a significant but challenging problem in many applications. Existing methods rely on ideal assumptions to estimate long-term average effects, e.g., no unobserved confounders or a binary treatment,while in numerous real-world applications, these assumptions could be violated and average effects are unable to provide individual-level suggestions.In this paper,we address a more general problem of estimating the long-term heterogeneous dose-response curve (HDRC) while accounting for unobserved confounders. Specifically, to remove unobserved confounding in observational data, we introduce an optimal transport weighting framework to align the observational data to the experimental data with theoretical guarantees. Furthermore,to accurately predict the heterogeneous effects of continuous treatment, we establish a generalization bound on counterfactual prediction error by leveraging the reweighted distribution induced by optimal transport. Finally, we develop an HDRC estimator building upon the above theoretical foundations. Extensive experimental studies conducted on multiple synthetic and semi-synthetic datasets demonstrate the effectiveness of our proposed method.
From Orthogonality to Dependency: Learning Disentangled Representation for Multi-Modal Time-Series Sensing Signals
May 25, 2024



Abstract:Existing methods for multi-modal time series representation learning aim to disentangle the modality-shared and modality-specific latent variables. Although achieving notable performances on downstream tasks, they usually assume an orthogonal latent space. However, the modality-specific and modality-shared latent variables might be dependent on real-world scenarios. Therefore, we propose a general generation process, where the modality-shared and modality-specific latent variables are dependent, and further develop a \textbf{M}ulti-mod\textbf{A}l \textbf{TE}mporal Disentanglement (\textbf{MATE}) model. Specifically, our \textbf{MATE} model is built on a temporally variational inference architecture with the modality-shared and modality-specific prior networks for the disentanglement of latent variables. Furthermore, we establish identifiability results to show that the extracted representation is disentangled. More specifically, we first achieve the subspace identifiability for modality-shared and modality-specific latent variables by leveraging the pairing of multi-modal data. Then we establish the component-wise identifiability of modality-specific latent variables by employing sufficient changes of historical latent variables. Extensive experimental studies on multi-modal sensors, human activity recognition, and healthcare datasets show a general improvement in different downstream tasks, highlighting the effectiveness of our method in real-world scenarios.
Doubly Robust Causal Effect Estimation under Networked Interference via Targeted Learning
May 06, 2024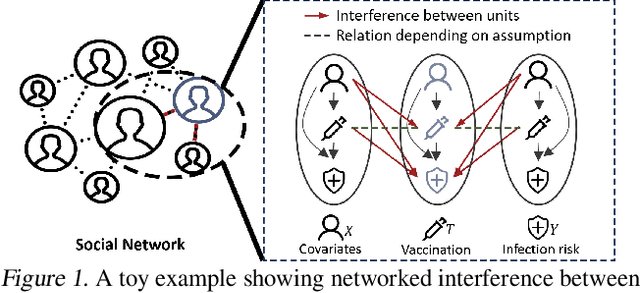
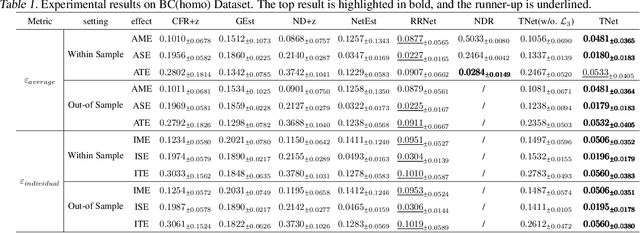
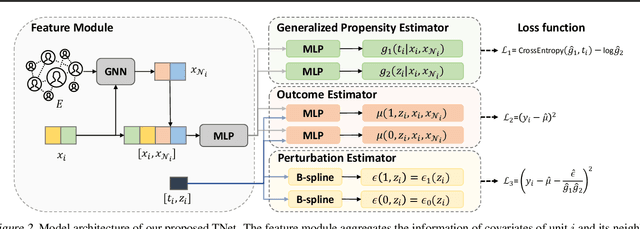
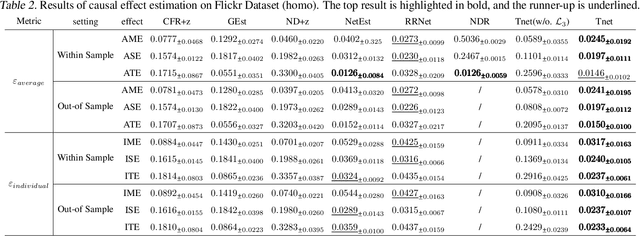
Abstract:Causal effect estimation under networked interference is an important but challenging problem. Available parametric methods are limited in their model space, while previous semiparametric methods, e.g., leveraging neural networks to fit only one single nuisance function, may still encounter misspecification problems under networked interference without appropriate assumptions on the data generation process. To mitigate bias stemming from misspecification, we propose a novel doubly robust causal effect estimator under networked interference, by adapting the targeted learning technique to the training of neural networks. Specifically, we generalize the targeted learning technique into the networked interference setting and establish the condition under which an estimator achieves double robustness. Based on the condition, we devise an end-to-end causal effect estimator by transforming the identified theoretical condition into a targeted loss. Moreover, we provide a theoretical analysis of our designed estimator, revealing a faster convergence rate compared to a single nuisance model. Extensive experimental results on two real-world networks with semisynthetic data demonstrate the effectiveness of our proposed estimators.
Generalization bound for estimating causal effects from observational network data
Aug 08, 2023Abstract:Estimating causal effects from observational network data is a significant but challenging problem. Existing works in causal inference for observational network data lack an analysis of the generalization bound, which can theoretically provide support for alleviating the complex confounding bias and practically guide the design of learning objectives in a principled manner. To fill this gap, we derive a generalization bound for causal effect estimation in network scenarios by exploiting 1) the reweighting schema based on joint propensity score and 2) the representation learning schema based on Integral Probability Metric (IPM). We provide two perspectives on the generalization bound in terms of reweighting and representation learning, respectively. Motivated by the analysis of the bound, we propose a weighting regression method based on the joint propensity score augmented with representation learning. Extensive experimental studies on two real-world networks with semi-synthetic data demonstrate the effectiveness of our algorithm.
Long-term Causal Effects Estimation via Latent Surrogates Representation Learning
Aug 09, 2022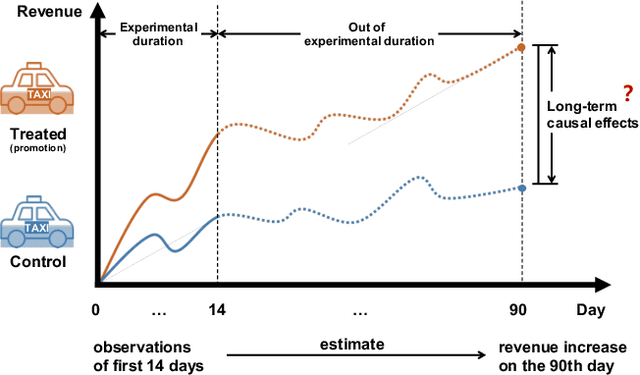
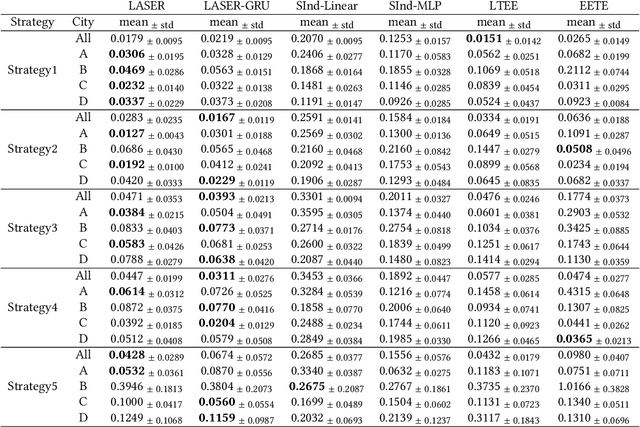
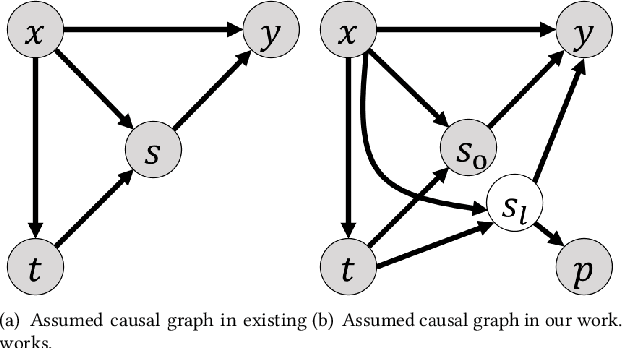
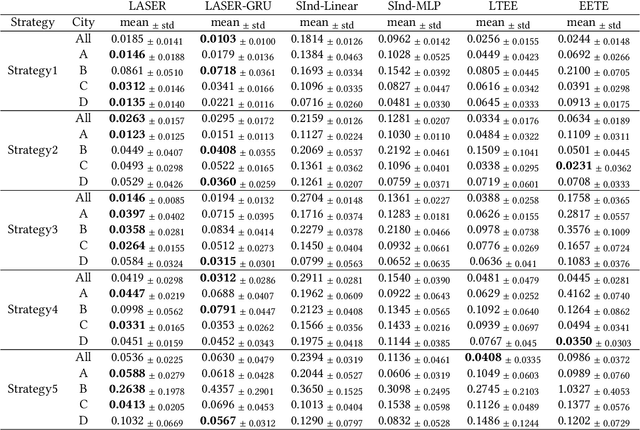
Abstract:Estimating long-term causal effects based on short-term surrogates is a significant but challenging problem in many real-world applications, e.g., marketing and medicine. Despite its success in certain domains, most existing methods estimate causal effects in an idealistic and simplistic way - ignoring the causal structure among short-term outcomes and treating all of them as surrogates. However, such methods cannot be well applied to real-world scenarios, in which the partially observed surrogates are mixed with their proxies among short-term outcomes. To this end, we develop our flexible method, Laser, to estimate long-term causal effects in the more realistic situation that the surrogates are observed or have observed proxies.Given the indistinguishability between the surrogates and proxies, we utilize identifiable variational auto-encoder (iVAE) to recover the whole valid surrogates on all the surrogates candidates without the need of distinguishing the observed surrogates or the proxies of latent surrogates. With the help of the recovered surrogates, we further devise an unbiased estimation of long-term causal effects. Extensive experimental results on the real-world and semi-synthetic datasets demonstrate the effectiveness of our proposed method.
On the Role of Entropy-based Loss for Learning Causal Structures with Continuous Optimization
Jun 17, 2021
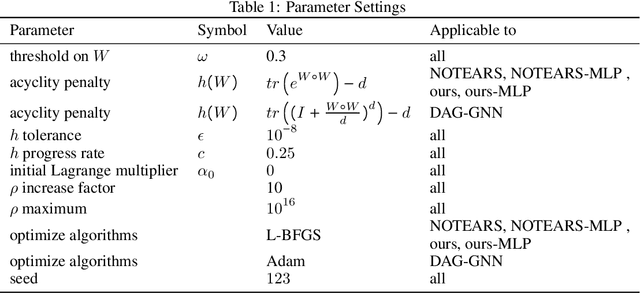
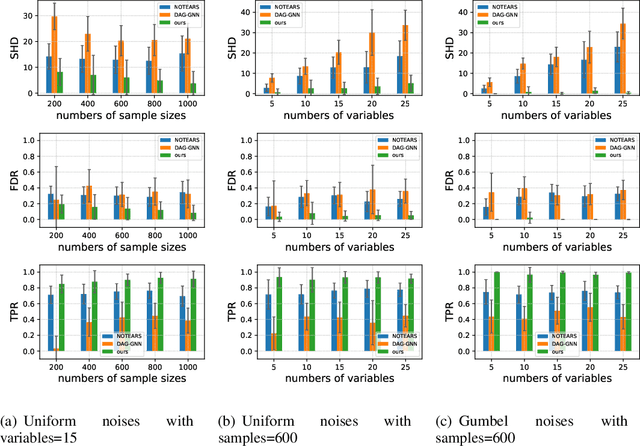
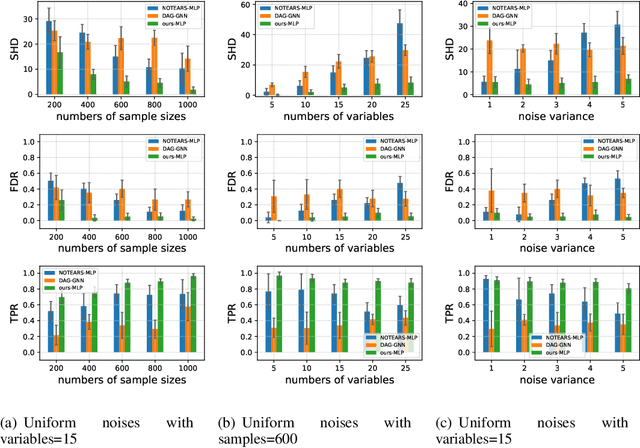
Abstract:Causal discovery from observational data is an important but challenging task in many scientific fields. Recently, NOTEARS [Zheng et al., 2018] formulates the causal structure learning problem as a continuous optimization problem using least-square loss with an acyclicity constraint. Though the least-square loss function is well justified under the standard Gaussian noise assumption, it is limited if the assumption does not hold. In this work, we theoretically show that the violation of the Gaussian noise assumption will hinder the causal direction identification, making the causal orientation fully determined by the causal strength as well as the variances of noises in the linear case and the noises of strong non-Gaussianity in the nonlinear case. Consequently, we propose a more general entropy-based loss that is theoretically consistent with the likelihood score under any noise distribution. We run extensive empirical evaluations on both synthetic data and real-world data to validate the effectiveness of the proposed method and show that our method achieves the best in Structure Hamming Distance, False Discovery Rate, and True Positive Rate matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge