Unifying Invariant and Variant Features for Graph Out-of-Distribution via Probability of Necessity and Sufficiency

Graph Out-of-Distribution (OOD), requiring that models trained on biased data generalize to the unseen test data, has considerable real-world applications. One of the most mainstream methods is to extract the invariant subgraph by aligning the original and augmented data with the help of environment augmentation. However, these solutions might lead to the loss or redundancy of semantic subgraphs and result in suboptimal generalization. To address this challenge, we propose exploiting Probability of Necessity and Sufficiency (PNS) to extract sufficient and necessary invariant substructures. Beyond that, we further leverage the domain variant subgraphs related to the labels to boost the generalization performance in an ensemble manner. Specifically, we first consider the data generation process for graph data. Under mild conditions, we show that the sufficient and necessary invariant subgraph can be extracted by minimizing an upper bound, built on the theoretical advance of the probability of necessity and sufficiency. To further bridge the theory and algorithm, we devise the model called Sufficiency and Necessity Inspired Graph Learning (SNIGL), which ensembles an invariant subgraph classifier on top of latent sufficient and necessary invariant subgraphs, and a domain variant subgraph classifier specific to the test domain for generalization enhancement. Experimental results demonstrate that our SNIGL model outperforms the state-of-the-art techniques on six public benchmarks, highlighting its effectiveness in real-world scenarios.

From Orthogonality to Dependency: Learning Disentangled Representation for Multi-Modal Time-Series Sensing Signals

Existing methods for multi-modal time series representation learning aim to disentangle the modality-shared and modality-specific latent variables. Although achieving notable performances on downstream tasks, they usually assume an orthogonal latent space. However, the modality-specific and modality-shared latent variables might be dependent on real-world scenarios. Therefore, we propose a general generation process, where the modality-shared and modality-specific latent variables are dependent, and further develop a \textbf{M}ulti-mod\textbf{A}l \textbf{TE}mporal Disentanglement (\textbf{MATE}) model. Specifically, our \textbf{MATE} model is built on a temporally variational inference architecture with the modality-shared and modality-specific prior networks for the disentanglement of latent variables. Furthermore, we establish identifiability results to show that the extracted representation is disentangled. More specifically, we first achieve the subspace identifiability for modality-shared and modality-specific latent variables by leveraging the pairing of multi-modal data. Then we establish the component-wise identifiability of modality-specific latent variables by employing sufficient changes of historical latent variables. Extensive experimental studies on multi-modal sensors, human activity recognition, and healthcare datasets show a general improvement in different downstream tasks, highlighting the effectiveness of our method in real-world scenarios.

Unifying Invariance and Spuriousity for Graph Out-of-Distribution via Probability of Necessity and Sufficiency

Graph Out-of-Distribution (OOD), requiring that models trained on biased data generalize to the unseen test data, has a massive of real-world applications. One of the most mainstream methods is to extract the invariant subgraph by aligning the original and augmented data with the help of environment augmentation. However, these solutions might lead to the loss or redundancy of semantic subgraph and further result in suboptimal generalization. To address this challenge, we propose a unified framework to exploit the Probability of Necessity and Sufficiency to extract the Invariant Substructure (PNSIS). Beyond that, this framework further leverages the spurious subgraph to boost the generalization performance in an ensemble manner to enhance the robustness on the noise data. Specificially, we first consider the data generation process for graph data. Under mild conditions, we show that the invariant subgraph can be extracted by minimizing an upper bound, which is built on the theoretical advance of probability of necessity and sufficiency. To further bridge the theory and algorithm, we devise the PNSIS model, which involves an invariant subgraph extractor for invariant graph learning as well invariant and spurious subgraph classifiers for generalization enhancement. Experimental results demonstrate that our \textbf{PNSIS} model outperforms the state-of-the-art techniques on graph OOD on several benchmarks, highlighting the effectiveness in real-world scenarios.

Feature Attribution with Necessity and Sufficiency via Dual-stage Perturbation Test for Causal Explanation

We investigate the problem of explainability in machine learning.To address this problem, Feature Attribution Methods (FAMs) measure the contribution of each feature through a perturbation test, where the difference in prediction is compared under different perturbations.However, such perturbation tests may not accurately distinguish the contributions of different features, when their change in prediction is the same after perturbation.In order to enhance the ability of FAMs to distinguish different features' contributions in this challenging setting, we propose to utilize the probability (PNS) that perturbing a feature is a necessary and sufficient cause for the prediction to change as a measure of feature importance.Our approach, Feature Attribution with Necessity and Sufficiency (FANS), computes the PNS via a perturbation test involving two stages (factual and interventional).In practice, to generate counterfactual samples, we use a resampling-based approach on the observed samples to approximate the required conditional distribution.Finally, we combine FANS and gradient-based optimization to extract the subset with the largest PNS.We demonstrate that FANS outperforms existing feature attribution methods on six benchmarks.

On the Probability of Necessity and Sufficiency of Explaining Graph Neural Networks: A Lower Bound Optimization Approach

Explainability of Graph Neural Networks (GNNs) is critical to various GNN applications but remains an open challenge. A convincing explanation should be both necessary and sufficient simultaneously. However, existing GNN explaining approaches focus on only one of the two aspects, necessity or sufficiency, or a trade-off between the two. To search for the most necessary and sufficient explanation, the Probability of Necessity and Sufficiency (PNS) can be applied since it can mathematically quantify the necessity and sufficiency of an explanation. Nevertheless, the difficulty of obtaining PNS due to non-monotonicity and the challenge of counterfactual estimation limits its wide use. To address the non-identifiability of PNS, we resort to a lower bound of PNS that can be optimized via counterfactual estimation, and propose Necessary and Sufficient Explanation for GNN (NSEG) via optimizing that lower bound. Specifically, we employ nearest neighbor matching to generate counterfactual samples for the features, which is different from the random perturbation. In particular, NSEG combines the edges and node features to generate an explanation, where the common edge explanation is a special case of the combined explanation. Empirical study shows that NSEG achieves excellent performance in generating the most necessary and sufficient explanations among a series of state-of-the-art methods.

Motif Graph Neural Network

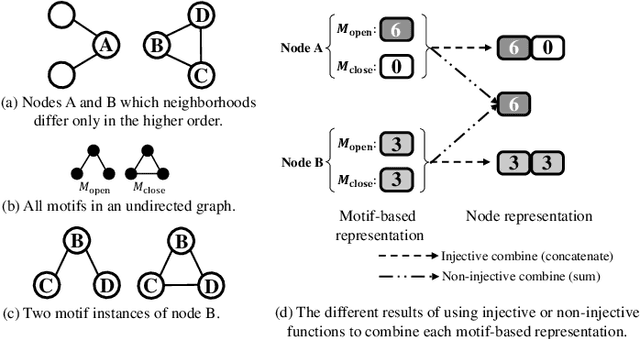
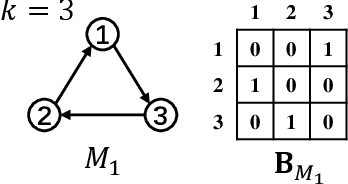
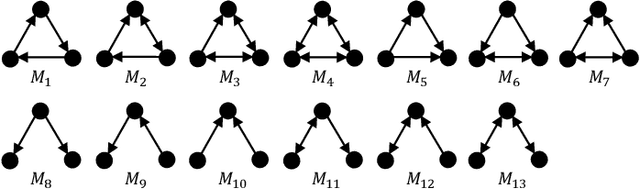
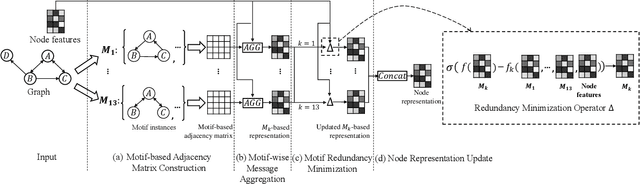
Graphs can model complicated interactions between entities, which naturally emerge in many important applications. These applications can often be cast into standard graph learning tasks, in which a crucial step is to learn low-dimensional graph representations. Graph neural networks (GNNs) are currently the most popular model in graph embedding approaches. However, standard GNNs in the neighborhood aggregation paradigm suffer from limited discriminative power in distinguishing \emph{high-order} graph structures as opposed to \emph{low-order} structures. To capture high-order structures, researchers have resorted to motifs and developed motif-based GNNs. However, existing motif-based GNNs still often suffer from less discriminative power on high-order structures. To overcome the above limitations, we propose Motif Graph Neural Network (MGNN), a novel framework to better capture high-order structures, hinging on our proposed motif redundancy minimization operator and injective motif combination. First, MGNN produces a set of node representations w.r.t. each motif. The next phase is our proposed redundancy minimization among motifs which compares the motifs with each other and distills the features unique to each motif. Finally, MGNN performs the updating of node representations by combining multiple representations from different motifs. In particular, to enhance the discriminative power, MGNN utilizes an injective function to combine the representations w.r.t. different motifs. We further show that our proposed architecture increases the expressive power of GNNs with a theoretical analysis. We demonstrate that MGNN outperforms state-of-the-art methods on seven public benchmarks on both node classification and graph classification tasks.