Learning Discrete Latent Variable Structures with Tensor Rank Conditions

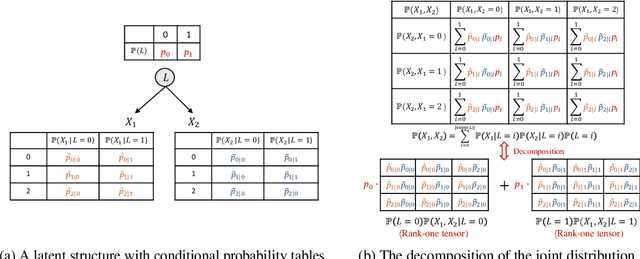
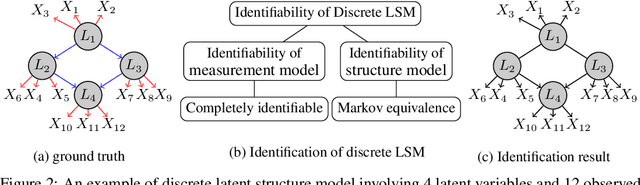
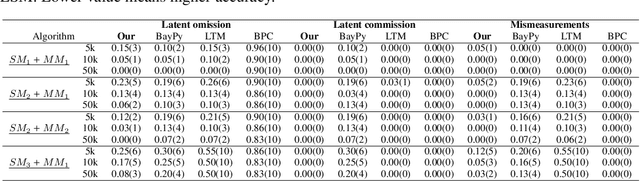
Unobserved discrete data are ubiquitous in many scientific disciplines, and how to learn the causal structure of these latent variables is crucial for uncovering data patterns. Most studies focus on the linear latent variable model or impose strict constraints on latent structures, which fail to address cases in discrete data involving non-linear relationships or complex latent structures. To achieve this, we explore a tensor rank condition on contingency tables for an observed variable set $\mathbf{X}_p$, showing that the rank is determined by the minimum support of a specific conditional set (not necessary in $\mathbf{X}_p$) that d-separates all variables in $\mathbf{X}_p$. By this, one can locate the latent variable through probing the rank on different observed variables set, and further identify the latent causal structure under some structure assumptions. We present the corresponding identification algorithm and conduct simulated experiments to verify the effectiveness of our method. In general, our results elegantly extend the identification boundary for causal discovery with discrete latent variables and expand the application scope of causal discovery with latent variables.

Doubly Robust Causal Effect Estimation under Networked Interference via Targeted Learning

Causal effect estimation under networked interference is an important but challenging problem. Available parametric methods are limited in their model space, while previous semiparametric methods, e.g., leveraging neural networks to fit only one single nuisance function, may still encounter misspecification problems under networked interference without appropriate assumptions on the data generation process. To mitigate bias stemming from misspecification, we propose a novel doubly robust causal effect estimator under networked interference, by adapting the targeted learning technique to the training of neural networks. Specifically, we generalize the targeted learning technique into the networked interference setting and establish the condition under which an estimator achieves double robustness. Based on the condition, we devise an end-to-end causal effect estimator by transforming the identified theoretical condition into a targeted loss. Moreover, we provide a theoretical analysis of our designed estimator, revealing a faster convergence rate compared to a single nuisance model. Extensive experimental results on two real-world networks with semisynthetic data demonstrate the effectiveness of our proposed estimators.

Causal Discovery from Poisson Branching Structural Causal Model Using High-Order Cumulant with Path Analysis

Count data naturally arise in many fields, such as finance, neuroscience, and epidemiology, and discovering causal structure among count data is a crucial task in various scientific and industrial scenarios. One of the most common characteristics of count data is the inherent branching structure described by a binomial thinning operator and an independent Poisson distribution that captures both branching and noise. For instance, in a population count scenario, mortality and immigration contribute to the count, where survival follows a Bernoulli distribution, and immigration follows a Poisson distribution. However, causal discovery from such data is challenging due to the non-identifiability issue: a single causal pair is Markov equivalent, i.e., $X\rightarrow Y$ and $Y\rightarrow X$ are distributed equivalent. Fortunately, in this work, we found that the causal order from $X$ to its child $Y$ is identifiable if $X$ is a root vertex and has at least two directed paths to $Y$, or the ancestor of $X$ with the most directed path to $X$ has a directed path to $Y$ without passing $X$. Specifically, we propose a Poisson Branching Structure Causal Model (PB-SCM) and perform a path analysis on PB-SCM using high-order cumulants. Theoretical results establish the connection between the path and cumulant and demonstrate that the path information can be obtained from the cumulant. With the path information, causal order is identifiable under some graphical conditions. A practical algorithm for learning causal structure under PB-SCM is proposed and the experiments demonstrate and verify the effectiveness of the proposed method.

Learning by Doing: An Online Causal Reinforcement Learning Framework with Causal-Aware Policy

As a key component to intuitive cognition and reasoning solutions in human intelligence, causal knowledge provides great potential for reinforcement learning (RL) agents' interpretability towards decision-making by helping reduce the searching space. However, there is still a considerable gap in discovering and incorporating causality into RL, which hinders the rapid development of causal RL. In this paper, we consider explicitly modeling the generation process of states with the causal graphical model, based on which we augment the policy. We formulate the causal structure updating into the RL interaction process with active intervention learning of the environment. To optimize the derived objective, we propose a framework with theoretical performance guarantees that alternates between two steps: using interventions for causal structure learning during exploration and using the learned causal structure for policy guidance during exploitation. Due to the lack of public benchmarks that allow direct intervention in the state space, we design the root cause localization task in our simulated fault alarm environment and then empirically show the effectiveness and robustness of the proposed method against state-of-the-art baselines. Theoretical analysis shows that our performance improvement attributes to the virtuous cycle of causal-guided policy learning and causal structure learning, which aligns with our experimental results.

Where and How to Attack? A Causality-Inspired Recipe for Generating Counterfactual Adversarial Examples

Deep neural networks (DNNs) have been demonstrated to be vulnerable to well-crafted \emph{adversarial examples}, which are generated through either well-conceived $\mathcal{L}_p$-norm restricted or unrestricted attacks. Nevertheless, the majority of those approaches assume that adversaries can modify any features as they wish, and neglect the causal generating process of the data, which is unreasonable and unpractical. For instance, a modification in income would inevitably impact features like the debt-to-income ratio within a banking system. By considering the underappreciated causal generating process, first, we pinpoint the source of the vulnerability of DNNs via the lens of causality, then give theoretical results to answer \emph{where to attack}. Second, considering the consequences of the attack interventions on the current state of the examples to generate more realistic adversarial examples, we propose CADE, a framework that can generate \textbf{C}ounterfactual \textbf{AD}versarial \textbf{E}xamples to answer \emph{how to attack}. The empirical results demonstrate CADE's effectiveness, as evidenced by its competitive performance across diverse attack scenarios, including white-box, transfer-based, and random intervention attacks.

Identification of Causal Structure in the Presence of Missing Data with Additive Noise Model

Missing data are an unavoidable complication frequently encountered in many causal discovery tasks. When a missing process depends on the missing values themselves (known as self-masking missingness), the recovery of the joint distribution becomes unattainable, and detecting the presence of such self-masking missingness remains a perplexing challenge. Consequently, due to the inability to reconstruct the original distribution and to discern the underlying missingness mechanism, simply applying existing causal discovery methods would lead to wrong conclusions. In this work, we found that the recent advances additive noise model has the potential for learning causal structure under the existence of the self-masking missingness. With this observation, we aim to investigate the identification problem of learning causal structure from missing data under an additive noise model with different missingness mechanisms, where the `no self-masking missingness' assumption can be eliminated appropriately. Specifically, we first elegantly extend the scope of identifiability of causal skeleton to the case with weak self-masking missingness (i.e., no other variable could be the cause of self-masking indicators except itself). We further provide the sufficient and necessary identification conditions of the causal direction under additive noise model and show that the causal structure can be identified up to an IN-equivalent pattern. We finally propose a practical algorithm based on the above theoretical results on learning the causal skeleton and causal direction. Extensive experiments on synthetic and real data demonstrate the efficiency and effectiveness of the proposed algorithms.

TNPAR: Topological Neural Poisson Auto-Regressive Model for Learning Granger Causal Structure from Event Sequences

Learning Granger causality from event sequences is a challenging but essential task across various applications. Most existing methods rely on the assumption that event sequences are independent and identically distributed (i.i.d.). However, this i.i.d. assumption is often violated due to the inherent dependencies among the event sequences. Fortunately, in practice, we find these dependencies can be modeled by a topological network, suggesting a potential solution to the non-i.i.d. problem by introducing the prior topological network into Granger causal discovery. This observation prompts us to tackle two ensuing challenges: 1) how to model the event sequences while incorporating both the prior topological network and the latent Granger causal structure, and 2) how to learn the Granger causal structure. To this end, we devise a two-stage unified topological neural Poisson auto-regressive model. During the generation stage, we employ a variant of the neural Poisson process to model the event sequences, considering influences from both the topological network and the Granger causal structure. In the inference stage, we formulate an amortized inference algorithm to infer the latent Granger causal structure. We encapsulate these two stages within a unified likelihood function, providing an end-to-end framework for this task.

Structural Hawkes Processes for Learning Causal Structure from Discrete-Time Event Sequences

Learning causal structure among event types from discrete-time event sequences is a particularly important but challenging task. Existing methods, such as the multivariate Hawkes processes based methods, mostly boil down to learning the so-called Granger causality which assumes that the cause event happens strictly prior to its effect event. Such an assumption is often untenable beyond applications, especially when dealing with discrete-time event sequences in low-resolution; and typical discrete Hawkes processes mainly suffer from identifiability issues raised by the instantaneous effect, i.e., the causal relationship that occurred simultaneously due to the low-resolution data will not be captured by Granger causality. In this work, we propose Structure Hawkes Processes (SHPs) that leverage the instantaneous effect for learning the causal structure among events type in discrete-time event sequence. The proposed method is featured with the minorization-maximization of the likelihood function and a sparse optimization scheme. Theoretical results show that the instantaneous effect is a blessing rather than a curse, and the causal structure is identifiable under the existence of the instantaneous effect. Experiments on synthetic and real-world data verify the effectiveness of the proposed method.

On the Probability of Necessity and Sufficiency of Explaining Graph Neural Networks: A Lower Bound Optimization Approach

Explainability of Graph Neural Networks (GNNs) is critical to various GNN applications but remains an open challenge. A convincing explanation should be both necessary and sufficient simultaneously. However, existing GNN explaining approaches focus on only one of the two aspects, necessity or sufficiency, or a trade-off between the two. To search for the most necessary and sufficient explanation, the Probability of Necessity and Sufficiency (PNS) can be applied since it can mathematically quantify the necessity and sufficiency of an explanation. Nevertheless, the difficulty of obtaining PNS due to non-monotonicity and the challenge of counterfactual estimation limits its wide use. To address the non-identifiability of PNS, we resort to a lower bound of PNS that can be optimized via counterfactual estimation, and propose Necessary and Sufficient Explanation for GNN (NSEG) via optimizing that lower bound. Specifically, we employ nearest neighbor matching to generate counterfactual samples for the features, which is different from the random perturbation. In particular, NSEG combines the edges and node features to generate an explanation, where the common edge explanation is a special case of the combined explanation. Empirical study shows that NSEG achieves excellent performance in generating the most necessary and sufficient explanations among a series of state-of-the-art methods.

REST: Debiased Social Recommendation via Reconstructing Exposure Strategies

The recommendation system, relying on historical observational data to model the complex relationships among the users and items, has achieved great success in real-world applications. Selection bias is one of the most important issues of the existing observational data based approaches, which is actually caused by multiple types of unobserved exposure strategies (e.g. promotions and holiday effects). Though various methods have been proposed to address this problem, they are mainly relying on the implicit debiasing techniques but not explicitly modeling the unobserved exposure strategies. By explicitly Reconstructing Exposure STrategies (REST in short), we formalize the recommendation problem as the counterfactual reasoning and propose the debiased social recommendation method. In REST, we assume that the exposure of an item is controlled by the latent exposure strategies, the user, and the item. Based on the above generation process, we first provide the theoretical guarantee of our method via identification analysis. Second, we employ a variational auto-encoder to reconstruct the latent exposure strategies, with the help of the social networks and the items. Third, we devise a counterfactual reasoning based recommendation algorithm by leveraging the recovered exposure strategies. Experiments on four real-world datasets, including three published datasets and one private WeChat Official Account dataset, demonstrate significant improvements over several state-of-the-art methods.