Learning Discrete Latent Variable Structures with Tensor Rank Conditions

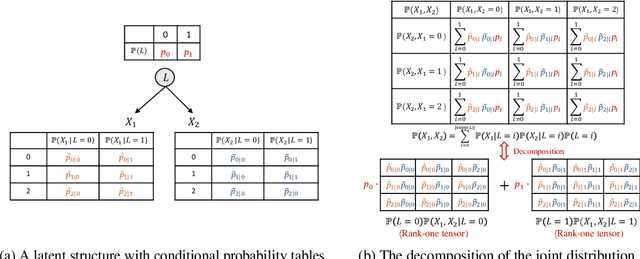
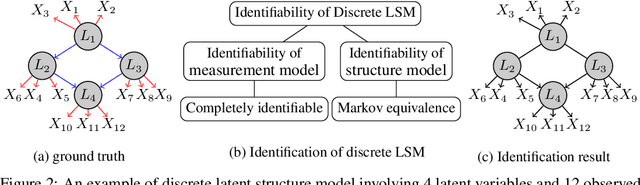
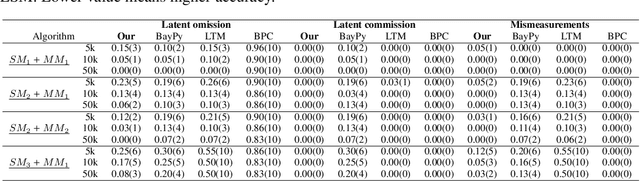
Unobserved discrete data are ubiquitous in many scientific disciplines, and how to learn the causal structure of these latent variables is crucial for uncovering data patterns. Most studies focus on the linear latent variable model or impose strict constraints on latent structures, which fail to address cases in discrete data involving non-linear relationships or complex latent structures. To achieve this, we explore a tensor rank condition on contingency tables for an observed variable set $\mathbf{X}_p$, showing that the rank is determined by the minimum support of a specific conditional set (not necessary in $\mathbf{X}_p$) that d-separates all variables in $\mathbf{X}_p$. By this, one can locate the latent variable through probing the rank on different observed variables set, and further identify the latent causal structure under some structure assumptions. We present the corresponding identification algorithm and conduct simulated experiments to verify the effectiveness of our method. In general, our results elegantly extend the identification boundary for causal discovery with discrete latent variables and expand the application scope of causal discovery with latent variables.

HateDebias: On the Diversity and Variability of Hate Speech Debiasing

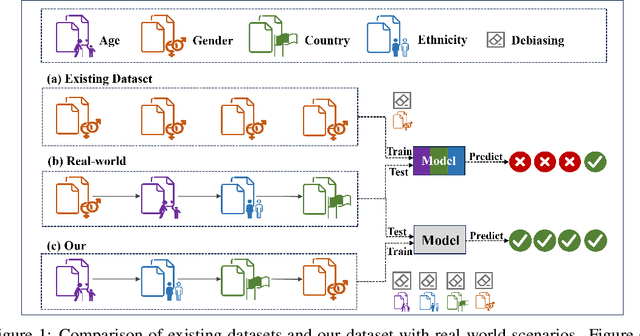
Hate speech on social media is ubiquitous but urgently controlled. Without detecting and mitigating the biases brought by hate speech, different types of ethical problems. While a number of datasets have been proposed to address the problem of hate speech detection, these datasets seldom consider the diversity and variability of bias, making it far from real-world scenarios. To fill this gap, we propose a benchmark, named HateDebias, to analyze the model ability of hate speech detection under continuous, changing environments. Specifically, to meet the diversity of biases, we collect existing hate speech detection datasets with different types of biases. To further meet the variability (i.e., the changing of bias attributes in datasets), we reorganize datasets to follow the continuous learning setting. We evaluate the detection accuracy of models trained on the datasets with a single type of bias with the performance on the HateDebias, where a significant performance drop is observed. To provide a potential direction for debiasing, we further propose a debiasing framework based on continuous learning and bias information regularization, as well as the memory replay strategies to ensure the debiasing ability of the model. Experiment results on the proposed benchmark show that the aforementioned method can improve several baselines with a distinguished margin, highlighting its effectiveness in real-world applications.

Automating the Selection of Proxy Variables of Unmeasured Confounders

Recently, interest has grown in the use of proxy variables of unobserved confounding for inferring the causal effect in the presence of unmeasured confounders from observational data. One difficulty inhibiting the practical use is finding valid proxy variables of unobserved confounding to a target causal effect of interest. These proxy variables are typically justified by background knowledge. In this paper, we investigate the estimation of causal effects among multiple treatments and a single outcome, all of which are affected by unmeasured confounders, within a linear causal model, without prior knowledge of the validity of proxy variables. To be more specific, we first extend the existing proxy variable estimator, originally addressing a single unmeasured confounder, to accommodate scenarios where multiple unmeasured confounders exist between the treatments and the outcome. Subsequently, we present two different sets of precise identifiability conditions for selecting valid proxy variables of unmeasured confounders, based on the second-order statistics and higher-order statistics of the data, respectively. Moreover, we propose two data-driven methods for the selection of proxy variables and for the unbiased estimation of causal effects. Theoretical analysis demonstrates the correctness of our proposed algorithms. Experimental results on both synthetic and real-world data show the effectiveness of the proposed approach.

Causal Discovery from Poisson Branching Structural Causal Model Using High-Order Cumulant with Path Analysis

Count data naturally arise in many fields, such as finance, neuroscience, and epidemiology, and discovering causal structure among count data is a crucial task in various scientific and industrial scenarios. One of the most common characteristics of count data is the inherent branching structure described by a binomial thinning operator and an independent Poisson distribution that captures both branching and noise. For instance, in a population count scenario, mortality and immigration contribute to the count, where survival follows a Bernoulli distribution, and immigration follows a Poisson distribution. However, causal discovery from such data is challenging due to the non-identifiability issue: a single causal pair is Markov equivalent, i.e., $X\rightarrow Y$ and $Y\rightarrow X$ are distributed equivalent. Fortunately, in this work, we found that the causal order from $X$ to its child $Y$ is identifiable if $X$ is a root vertex and has at least two directed paths to $Y$, or the ancestor of $X$ with the most directed path to $X$ has a directed path to $Y$ without passing $X$. Specifically, we propose a Poisson Branching Structure Causal Model (PB-SCM) and perform a path analysis on PB-SCM using high-order cumulants. Theoretical results establish the connection between the path and cumulant and demonstrate that the path information can be obtained from the cumulant. With the path information, causal order is identifiable under some graphical conditions. A practical algorithm for learning causal structure under PB-SCM is proposed and the experiments demonstrate and verify the effectiveness of the proposed method.

When and How: Learning Identifiable Latent States for Nonstationary Time Series Forecasting

Temporal distribution shifts are ubiquitous in time series data. One of the most popular methods assumes that the temporal distribution shift occurs uniformly to disentangle the stationary and nonstationary dependencies. But this assumption is difficult to meet, as we do not know when the distribution shifts occur. To solve this problem, we propose to learn IDentifiable latEnt stAtes (IDEA) to detect when the distribution shifts occur. Beyond that, we further disentangle the stationary and nonstationary latent states via sufficient observation assumption to learn how the latent states change. Specifically, we formalize the causal process with environment-irrelated stationary and environment-related nonstationary variables. Under mild conditions, we show that latent environments and stationary/nonstationary variables are identifiable. Based on these theories, we devise the IDEA model, which incorporates an autoregressive hidden Markov model to estimate latent environments and modular prior networks to identify latent states. The IDEA model outperforms several latest nonstationary forecasting methods on various benchmark datasets, highlighting its advantages in real-world scenarios.

Identification of Causal Structure in the Presence of Missing Data with Additive Noise Model

Missing data are an unavoidable complication frequently encountered in many causal discovery tasks. When a missing process depends on the missing values themselves (known as self-masking missingness), the recovery of the joint distribution becomes unattainable, and detecting the presence of such self-masking missingness remains a perplexing challenge. Consequently, due to the inability to reconstruct the original distribution and to discern the underlying missingness mechanism, simply applying existing causal discovery methods would lead to wrong conclusions. In this work, we found that the recent advances additive noise model has the potential for learning causal structure under the existence of the self-masking missingness. With this observation, we aim to investigate the identification problem of learning causal structure from missing data under an additive noise model with different missingness mechanisms, where the `no self-masking missingness' assumption can be eliminated appropriately. Specifically, we first elegantly extend the scope of identifiability of causal skeleton to the case with weak self-masking missingness (i.e., no other variable could be the cause of self-masking indicators except itself). We further provide the sufficient and necessary identification conditions of the causal direction under additive noise model and show that the causal structure can be identified up to an IN-equivalent pattern. We finally propose a practical algorithm based on the above theoretical results on learning the causal skeleton and causal direction. Extensive experiments on synthetic and real data demonstrate the efficiency and effectiveness of the proposed algorithms.

Generalized Independent Noise Condition for Estimating Causal Structure with Latent Variables

We investigate the challenging task of learning causal structure in the presence of latent variables, including locating latent variables and determining their quantity, and identifying causal relationships among both latent and observed variables. To address this, we propose a Generalized Independent Noise (GIN) condition for linear non-Gaussian acyclic causal models that incorporate latent variables, which establishes the independence between a linear combination of certain measured variables and some other measured variables. Specifically, for two observed random vectors $\bf{Y}$ and $\bf{Z}$, GIN holds if and only if $\omega^{\intercal}\mathbf{Y}$ and $\mathbf{Z}$ are independent, where $\omega$ is a non-zero parameter vector determined by the cross-covariance between $\mathbf{Y}$ and $\mathbf{Z}$. We then give necessary and sufficient graphical criteria of the GIN condition in linear non-Gaussian acyclic causal models. Roughly speaking, GIN implies the existence of an exogenous set $\mathcal{S}$ relative to the parent set of $\mathbf{Y}$ (w.r.t. the causal ordering), such that $\mathcal{S}$ d-separates $\mathbf{Y}$ from $\mathbf{Z}$. Interestingly, we find that the independent noise condition (i.e., if there is no confounder, causes are independent of the residual derived from regressing the effect on the causes) can be seen as a special case of GIN. With such a connection between GIN and latent causal structures, we further leverage the proposed GIN condition, together with a well-designed search procedure, to efficiently estimate Linear, Non-Gaussian Latent Hierarchical Models (LiNGLaHs), where latent confounders may also be causally related and may even follow a hierarchical structure. We show that the underlying causal structure of a LiNGLaH is identifiable in light of GIN conditions under mild assumptions. Experimental results show the effectiveness of the proposed approach.