Local Learning for Covariate Selection in Nonparametric Causal Effect Estimation with Latent Variables

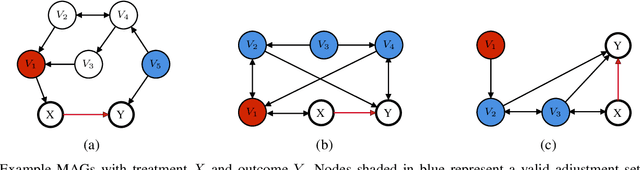
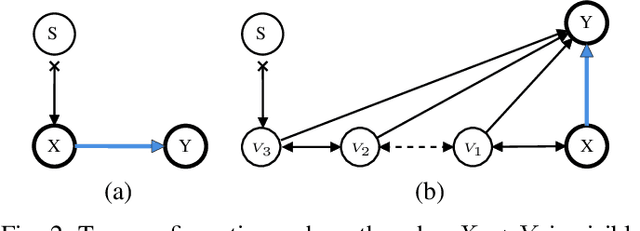
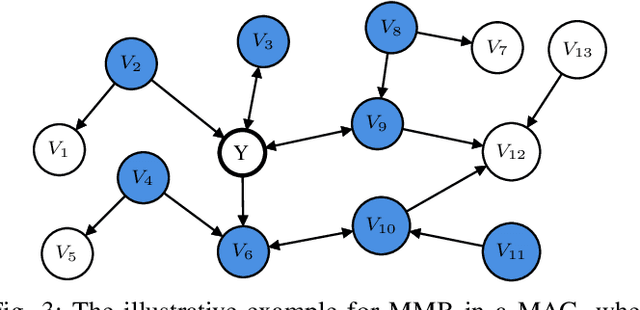
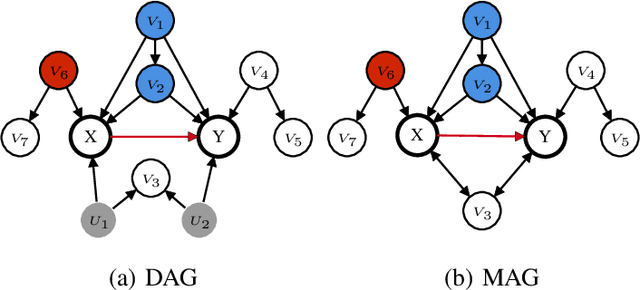
Estimating causal effects from nonexperimental data is a fundamental problem in many fields of science. A key component of this task is selecting an appropriate set of covariates for confounding adjustment to avoid bias. Most existing methods for covariate selection often assume the absence of latent variables and rely on learning the global network structure among variables. However, identifying the global structure can be unnecessary and inefficient, especially when our primary interest lies in estimating the effect of a treatment variable on an outcome variable. To address this limitation, we propose a novel local learning approach for covariate selection in nonparametric causal effect estimation, which accounts for the presence of latent variables. Our approach leverages testable independence and dependence relationships among observed variables to identify a valid adjustment set for a target causal relationship, ensuring both soundness and completeness under standard assumptions. We validate the effectiveness of our algorithm through extensive experiments on both synthetic and real-world data.

Testability of Instrumental Variables in Additive Nonlinear, Non-Constant Effects Models

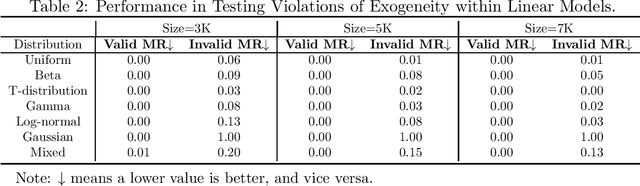
We address the issue of the testability of instrumental variables derived from observational data. Most existing testable implications are centered on scenarios where the treatment is a discrete variable, e.g., instrumental inequality (Pearl, 1995), or where the effect is assumed to be constant, e.g., instrumental variables condition based on the principle of independent mechanisms (Burauel, 2023). However, treatments can often be continuous variables, such as drug dosages or nutritional content levels, and non-constant effects may occur in many real-world scenarios. In this paper, we consider an additive nonlinear, non-constant effects model with unmeasured confounders, in which treatments can be either discrete or continuous, and propose an Auxiliary-based Independence Test (AIT) condition to test whether a variable is a valid instrument. We first show that if the candidate instrument is valid, then the AIT condition holds. Moreover, we illustrate the implications of the AIT condition and demonstrate that, in certain conditions, AIT conditions are necessary and sufficient to detect all invalid IVs. We also extend the AIT condition to include covariates and introduce a practical testing algorithm. Experimental results on both synthetic and three different real-world datasets show the effectiveness of our proposed condition.

Identification and Estimation of the Bi-Directional MR with Some Invalid Instruments

We consider the challenging problem of estimating causal effects from purely observational data in the bi-directional Mendelian randomization (MR), where some invalid instruments, as well as unmeasured confounding, usually exist. To address this problem, most existing methods attempt to find proper valid instrumental variables (IVs) for the target causal effect by expert knowledge or by assuming that the causal model is a one-directional MR model. As such, in this paper, we first theoretically investigate the identification of the bi-directional MR from observational data. In particular, we provide necessary and sufficient conditions under which valid IV sets are correctly identified such that the bi-directional MR model is identifiable, including the causal directions of a pair of phenotypes (i.e., the treatment and outcome). Moreover, based on the identification theory, we develop a cluster fusion-like method to discover valid IV sets and estimate the causal effects of interest. We theoretically demonstrate the correctness of the proposed algorithm. Experimental results show the effectiveness of our method for estimating causal effects in bi-directional MR.

Local Causal Structure Learning in the Presence of Latent Variables

Discovering causal relationships from observational data, particularly in the presence of latent variables, poses a challenging problem. While current local structure learning methods have proven effective and efficient when the focus lies solely on the local relationships of a target variable, they operate under the assumption of causal sufficiency. This assumption implies that all the common causes of the measured variables are observed, leaving no room for latent variables. Such a premise can be easily violated in various real-world applications, resulting in inaccurate structures that may adversely impact downstream tasks. In light of this, our paper delves into the primary investigation of locally identifying potential parents and children of a target from observational data that may include latent variables. Specifically, we harness the causal information from m-separation and V-structures to derive theoretical consistency results, effectively bridging the gap between global and local structure learning. Together with the newly developed stop rules, we present a principled method for determining whether a variable is a direct cause or effect of a target. Further, we theoretically demonstrate the correctness of our approach under the standard causal Markov and faithfulness conditions, with infinite samples. Experimental results on both synthetic and real-world data validate the effectiveness and efficiency of our approach.

Automating the Selection of Proxy Variables of Unmeasured Confounders

Recently, interest has grown in the use of proxy variables of unobserved confounding for inferring the causal effect in the presence of unmeasured confounders from observational data. One difficulty inhibiting the practical use is finding valid proxy variables of unobserved confounding to a target causal effect of interest. These proxy variables are typically justified by background knowledge. In this paper, we investigate the estimation of causal effects among multiple treatments and a single outcome, all of which are affected by unmeasured confounders, within a linear causal model, without prior knowledge of the validity of proxy variables. To be more specific, we first extend the existing proxy variable estimator, originally addressing a single unmeasured confounder, to accommodate scenarios where multiple unmeasured confounders exist between the treatments and the outcome. Subsequently, we present two different sets of precise identifiability conditions for selecting valid proxy variables of unmeasured confounders, based on the second-order statistics and higher-order statistics of the data, respectively. Moreover, we propose two data-driven methods for the selection of proxy variables and for the unbiased estimation of causal effects. Theoretical analysis demonstrates the correctness of our proposed algorithms. Experimental results on both synthetic and real-world data show the effectiveness of the proposed approach.

Debiased Collaborative Filtering with Kernel-Based Causal Balancing

Debiased collaborative filtering aims to learn an unbiased prediction model by removing different biases in observational datasets. To solve this problem, one of the simple and effective methods is based on the propensity score, which adjusts the observational sample distribution to the target one by reweighting observed instances. Ideally, propensity scores should be learned with causal balancing constraints. However, existing methods usually ignore such constraints or implement them with unreasonable approximations, which may affect the accuracy of the learned propensity scores. To bridge this gap, in this paper, we first analyze the gaps between the causal balancing requirements and existing methods such as learning the propensity with cross-entropy loss or manually selecting functions to balance. Inspired by these gaps, we propose to approximate the balancing functions in reproducing kernel Hilbert space and demonstrate that, based on the universal property and representer theorem of kernel functions, the causal balancing constraints can be better satisfied. Meanwhile, we propose an algorithm that adaptively balances the kernel function and theoretically analyze the generalization error bound of our methods. We conduct extensive experiments to demonstrate the effectiveness of our methods, and to promote this research direction, we have released our project at https://github.com/haoxuanli-pku/ICLR24-Kernel-Balancing.

Be Aware of the Neighborhood Effect: Modeling Selection Bias under Interference

Selection bias in recommender system arises from the recommendation process of system filtering and the interactive process of user selection. Many previous studies have focused on addressing selection bias to achieve unbiased learning of the prediction model, but ignore the fact that potential outcomes for a given user-item pair may vary with the treatments assigned to other user-item pairs, named neighborhood effect. To fill the gap, this paper formally formulates the neighborhood effect as an interference problem from the perspective of causal inference and introduces a treatment representation to capture the neighborhood effect. On this basis, we propose a novel ideal loss that can be used to deal with selection bias in the presence of neighborhood effect. We further develop two new estimators for estimating the proposed ideal loss. We theoretically establish the connection between the proposed and previous debiasing methods ignoring the neighborhood effect, showing that the proposed methods can achieve unbiased learning when both selection bias and neighborhood effect are present, while the existing methods are biased. Extensive semi-synthetic and real-world experiments are conducted to demonstrate the effectiveness of the proposed methods.

Generalized Independent Noise Condition for Estimating Causal Structure with Latent Variables

We investigate the challenging task of learning causal structure in the presence of latent variables, including locating latent variables and determining their quantity, and identifying causal relationships among both latent and observed variables. To address this, we propose a Generalized Independent Noise (GIN) condition for linear non-Gaussian acyclic causal models that incorporate latent variables, which establishes the independence between a linear combination of certain measured variables and some other measured variables. Specifically, for two observed random vectors $\bf{Y}$ and $\bf{Z}$, GIN holds if and only if $\omega^{\intercal}\mathbf{Y}$ and $\mathbf{Z}$ are independent, where $\omega$ is a non-zero parameter vector determined by the cross-covariance between $\mathbf{Y}$ and $\mathbf{Z}$. We then give necessary and sufficient graphical criteria of the GIN condition in linear non-Gaussian acyclic causal models. Roughly speaking, GIN implies the existence of an exogenous set $\mathcal{S}$ relative to the parent set of $\mathbf{Y}$ (w.r.t. the causal ordering), such that $\mathcal{S}$ d-separates $\mathbf{Y}$ from $\mathbf{Z}$. Interestingly, we find that the independent noise condition (i.e., if there is no confounder, causes are independent of the residual derived from regressing the effect on the causes) can be seen as a special case of GIN. With such a connection between GIN and latent causal structures, we further leverage the proposed GIN condition, together with a well-designed search procedure, to efficiently estimate Linear, Non-Gaussian Latent Hierarchical Models (LiNGLaHs), where latent confounders may also be causally related and may even follow a hierarchical structure. We show that the underlying causal structure of a LiNGLaH is identifiable in light of GIN conditions under mild assumptions. Experimental results show the effectiveness of the proposed approach.

Modeling High-Dimensional Data with Unknown Cut Points: A Fusion Penalized Logistic Threshold Regression

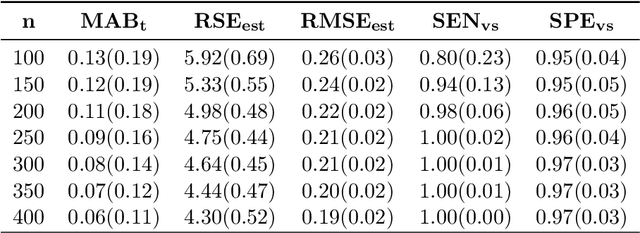
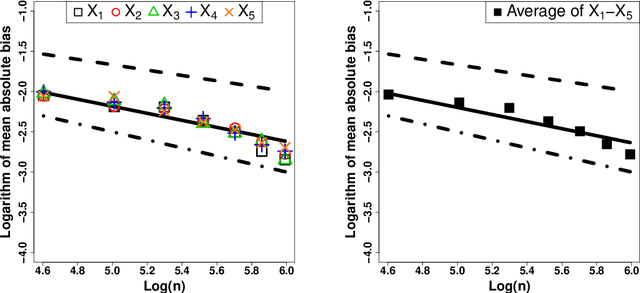
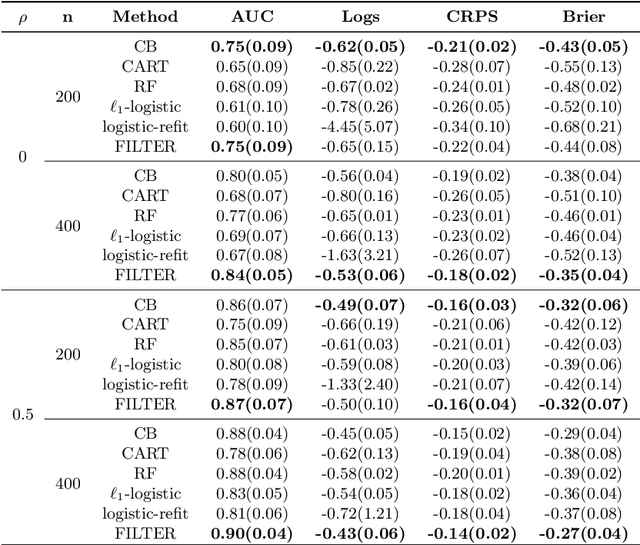
In traditional logistic regression models, the link function is often assumed to be linear and continuous in predictors. Here, we consider a threshold model that all continuous features are discretized into ordinal levels, which further determine the binary responses. Both the threshold points and regression coefficients are unknown and to be estimated. For high dimensional data, we propose a fusion penalized logistic threshold regression (FILTER) model, where a fused lasso penalty is employed to control the total variation and shrink the coefficients to zero as a method of variable selection. Under mild conditions on the estimate of unknown threshold points, we establish the non-asymptotic error bound for coefficient estimation and the model selection consistency. With a careful characterization of the error propagation, we have also shown that the tree-based method, such as CART, fulfill the threshold estimation conditions. We find the FILTER model is well suited in the problem of early detection and prediction for chronic disease like diabetes, using physical examination data. The finite sample behavior of our proposed method are also explored and compared with extensive Monte Carlo studies, which supports our theoretical discoveries.

A Local Method for Identifying Causal Relations under Markov Equivalence

Causality is important for designing interpretable and robust methods in artificial intelligence research. We propose a local approach to identify whether a variable is a cause of a given target based on causal graphical models of directed acyclic graphs (DAGs). In general, the causal relation between two variables may not be identifiable from observational data as many causal DAGs encoding different causal relations are Markov equivalent. In this paper, we first introduce a sufficient and necessary graphical condition to check the existence of a causal path from a variable to a target in every Markov equivalent DAG. Next, we provide local criteria for identifying whether the variable is a cause/non-cause of the target. Finally, we propose a local learning algorithm for this causal query via learning local structure of the variable and some additional statistical independence tests related to the target. Simulation studies show that our local algorithm is efficient and effective, compared with other state-of-art methods.