Zhuangyan Fang
On the Representation of Causal Background Knowledge and its Applications in Causal Inference
Jul 10, 2022

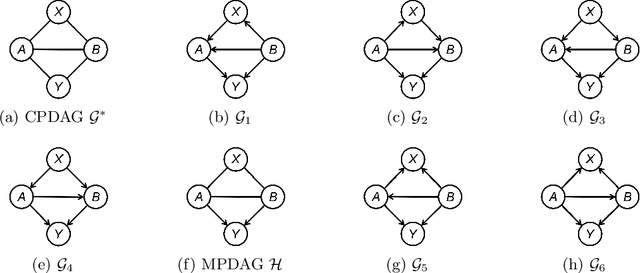

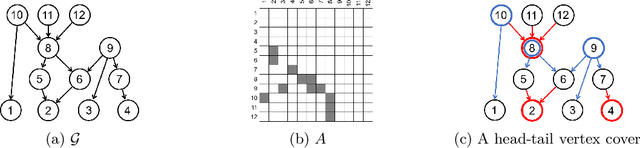
Abstract:Causal background knowledge about the existence or the absence of causal edges and paths is frequently encountered in observational studies. The shared directed edges and links of a subclass of Markov equivalent DAGs refined due to background knowledge can be represented by a causal maximally partially directed acyclic graph (MPDAG). In this paper, we first provide a sound and complete graphical characterization of causal MPDAGs and give a minimal representation of a causal MPDAG. Then, we introduce a novel representation called direct causal clause (DCC) to represent all types of causal background knowledge in a unified form. Using DCCs, we study the consistency and equivalency of causal background knowledge and show that any causal background knowledge set can be equivalently decomposed into a causal MPDAG plus a minimal residual set of DCCs. Polynomial-time algorithms are also provided for checking the consistency, equivalency, and finding the decomposed MPDAG and residual DCCs. Finally, with causal background knowledge, we prove a sufficient and necessary condition to identify causal effects and surprisingly find that the identifiability of causal effects only depends on the decomposed MPDAG. We also develop a local IDA-type algorithm to estimate the possible values of an unidentifiable effect. Simulations suggest that causal background knowledge can significantly improve the identifiability of causal effects.
A Local Method for Identifying Causal Relations under Markov Equivalence
Feb 25, 2021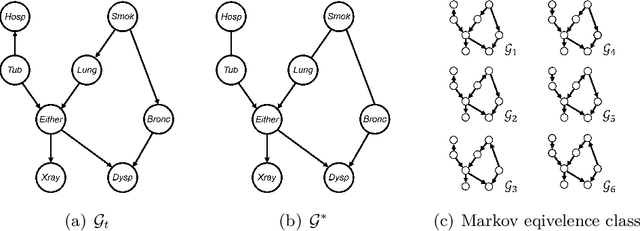
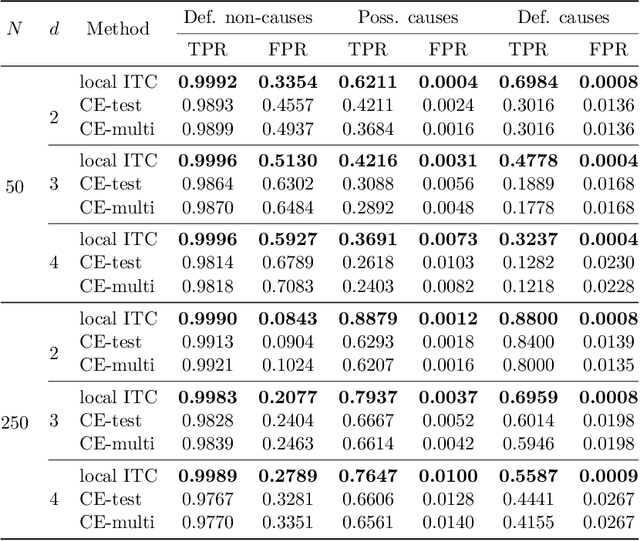
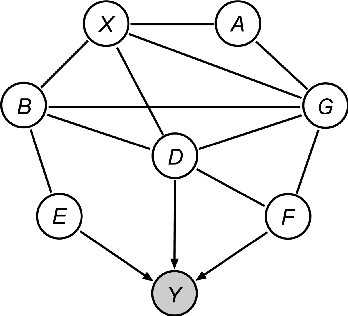
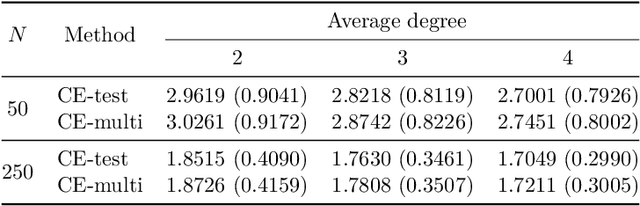
Abstract:Causality is important for designing interpretable and robust methods in artificial intelligence research. We propose a local approach to identify whether a variable is a cause of a given target based on causal graphical models of directed acyclic graphs (DAGs). In general, the causal relation between two variables may not be identifiable from observational data as many causal DAGs encoding different causal relations are Markov equivalent. In this paper, we first introduce a sufficient and necessary graphical condition to check the existence of a causal path from a variable to a target in every Markov equivalent DAG. Next, we provide local criteria for identifying whether the variable is a cause/non-cause of the target. Finally, we propose a local learning algorithm for this causal query via learning local structure of the variable and some additional statistical independence tests related to the target. Simulation studies show that our local algorithm is efficient and effective, compared with other state-of-art methods.
Low Rank Directed Acyclic Graphs and Causal Structure Learning
Jun 10, 2020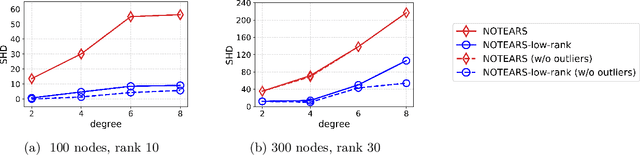
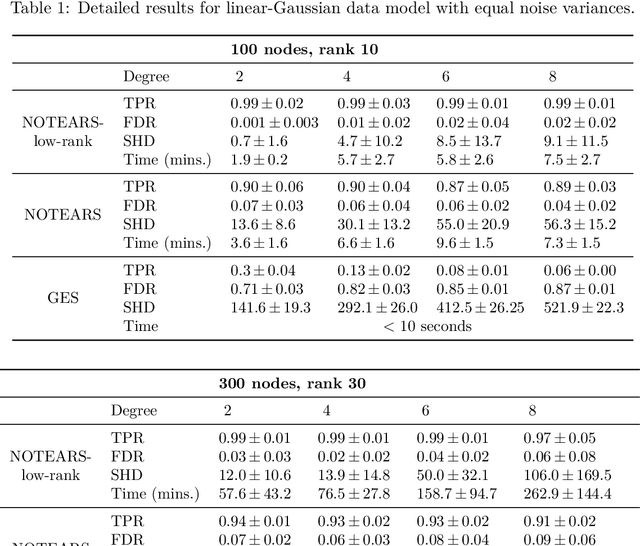
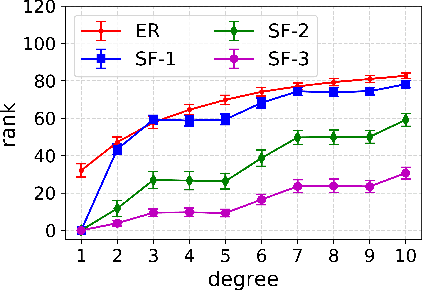
Abstract:Despite several important advances in recent years, learning causal structures represented by directed acyclic graphs (DAGs) remains a challenging task in high dimensional settings when the graphs to be learned are not sparse. In particular, the recent formulation of structure learning as a continuous optimization problem proved to have considerable advantages over the traditional combinatorial formulation, but the performance of the resulting algorithms is still wanting when the target graph is relatively large and dense. In this paper we propose a novel approach to mitigate this problem, by exploiting a low rank assumption regarding the (weighted) adjacency matrix of a DAG causal model. We establish several useful results relating interpretable graphical conditions to the low rank assumption, and show how to adapt existing methods for causal structure learning to take advantage of this assumption. We also provide empirical evidence for the utility of our low rank algorithms, especially on graphs that are not sparse. Not only do they outperform state-of-the-art algorithms when the low rank condition is satisfied, the performance on randomly generated scale-free graphs is also very competitive even though the true ranks may not be as low as is assumed.
A Graph Autoencoder Approach to Causal Structure Learning
Nov 18, 2019


Abstract:Causal structure learning has been a challenging task in the past decades and several mainstream approaches such as constraint- and score-based methods have been studied with theoretical guarantees. Recently, a new approach has transformed the combinatorial structure learning problem into a continuous one and then solved it using gradient-based optimization methods. Following the recent state-of-the-arts, we propose a new gradient-based method to learn causal structures from observational data. The proposed method generalizes the recent gradient-based methods to a graph autoencoder framework that allows nonlinear structural equation models and is easily applicable to vector-valued variables. We demonstrate that on synthetic datasets, our proposed method outperforms other gradient-based methods significantly, especially on large causal graphs. We further investigate the scalability and efficiency of our method, and observe a near linear training time when scaling up the graph size.
Masked Gradient-Based Causal Structure Learning
Oct 18, 2019



Abstract:Learning causal graphical models based on directed acyclic graphs is an important task in causal discovery and causal inference. We consider a general framework towards efficient causal structure learning with potentially large graphs. Within this framework, we propose a masked gradient-based structure learning method based on binary adjacency matrix that exists for any structural equation model. To enable first-order optimization methods, we use Gumbel-Softmax approach to approximate the binary valued entries of the adjacency matrix, which usually results in real values that are close to zero or one. The proposed method can readily include any differentiable score function and model function for learning causal structures. Experiments on both synthetic and real-world datasets are conducted to show the effectiveness of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge