Latent Variable Causal Discovery under Selection Bias

Addressing selection bias in latent variable causal discovery is important yet underexplored, largely due to a lack of suitable statistical tools: While various tools beyond basic conditional independencies have been developed to handle latent variables, none have been adapted for selection bias. We make an attempt by studying rank constraints, which, as a generalization to conditional independence constraints, exploits the ranks of covariance submatrices in linear Gaussian models. We show that although selection can significantly complicate the joint distribution, interestingly, the ranks in the biased covariance matrices still preserve meaningful information about both causal structures and selection mechanisms. We provide a graph-theoretic characterization of such rank constraints. Using this tool, we demonstrate that the one-factor model, a classical latent variable model, can be identified under selection bias. Simulations and real-world experiments confirm the effectiveness of using our rank constraints.

Higher-Order Causal Structure Learning with Additive Models

Causal structure learning has long been the central task of inferring causal insights from data. Despite the abundance of real-world processes exhibiting higher-order mechanisms, however, an explicit treatment of interactions in causal discovery has received little attention. In this work, we focus on extending the causal additive model (CAM) to additive models with higher-order interactions. This second level of modularity we introduce to the structure learning problem is most easily represented by a directed acyclic hypergraph which extends the DAG. We introduce the necessary definitions and theoretical tools to handle the novel structure we introduce and then provide identifiability results for the hyper DAG, extending the typical Markov equivalence classes. We next provide insights into why learning the more complex hypergraph structure may actually lead to better empirical results. In particular, more restrictive assumptions like CAM correspond to easier-to-learn hyper DAGs and better finite sample complexity. We finally develop an extension of the greedy CAM algorithm which can handle the more complex hyper DAG search space and demonstrate its empirical usefulness in synthetic experiments.

Score-based Greedy Search for Structure Identification of Partially Observed Linear Causal Models

Identifying the structure of a partially observed causal system is essential to various scientific fields. Recent advances have focused on constraint-based causal discovery to solve this problem, and yet in practice these methods often face challenges related to multiple testing and error propagation. These issues could be mitigated by a score-based method and thus it has raised great attention whether there exists a score-based greedy search method that can handle the partially observed scenario. In this work, we propose the first score-based greedy search method for the identification of structure involving latent variables with identifiability guarantees. Specifically, we propose Generalized N Factor Model and establish the global consistency: the true structure including latent variables can be identified up to the Markov equivalence class by using score. We then design Latent variable Greedy Equivalence Search (LGES), a greedy search algorithm for this class of model with well-defined operators, which search very efficiently over the graph space to find the optimal structure. Our experiments on both synthetic and real-life data validate the effectiveness of our method (code will be publicly available).

Analytic DAG Constraints for Differentiable DAG Learning

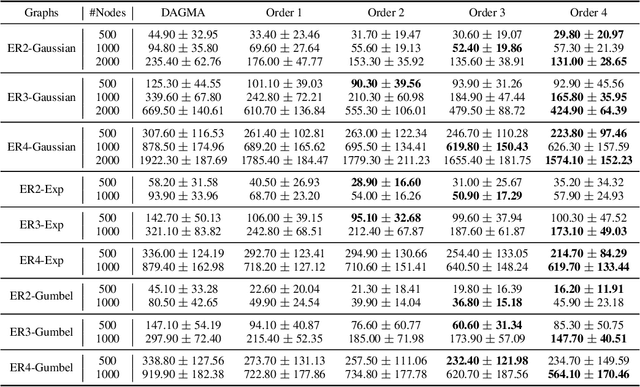
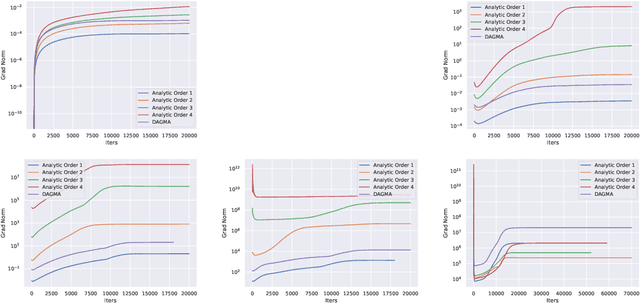
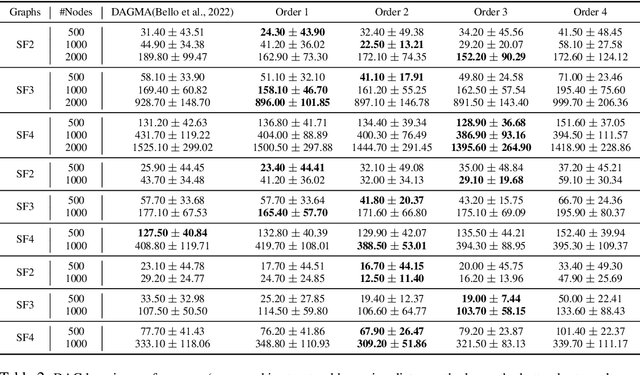
Recovering the underlying Directed Acyclic Graph (DAG) structures from observational data presents a formidable challenge, partly due to the combinatorial nature of the DAG-constrained optimization problem. Recently, researchers have identified gradient vanishing as one of the primary obstacles in differentiable DAG learning and have proposed several DAG constraints to mitigate this issue. By developing the necessary theory to establish a connection between analytic functions and DAG constraints, we demonstrate that analytic functions from the set $\{f(x) = c_0 + \sum_{i=1}^{\infty}c_ix^i | \forall i > 0, c_i > 0; r = \lim_{i\rightarrow \infty}c_{i}/c_{i+1} > 0\}$ can be employed to formulate effective DAG constraints. Furthermore, we establish that this set of functions is closed under several functional operators, including differentiation, summation, and multiplication. Consequently, these operators can be leveraged to create novel DAG constraints based on existing ones. Using these properties, we design a series of DAG constraints and develop an efficient algorithm to evaluate them. Experiments in various settings demonstrate that our DAG constraints outperform previous state-of-the-art comparators. Our implementation is available at https://github.com/zzhang1987/AnalyticDAGLearning.

When Selection Meets Intervention: Additional Complexities in Causal Discovery

We address the common yet often-overlooked selection bias in interventional studies, where subjects are selectively enrolled into experiments. For instance, participants in a drug trial are usually patients of the relevant disease; A/B tests on mobile applications target existing users only, and gene perturbation studies typically focus on specific cell types, such as cancer cells. Ignoring this bias leads to incorrect causal discovery results. Even when recognized, the existing paradigm for interventional causal discovery still fails to address it. This is because subtle differences in when and where interventions happen can lead to significantly different statistical patterns. We capture this dynamic by introducing a graphical model that explicitly accounts for both the observed world (where interventions are applied) and the counterfactual world (where selection occurs while interventions have not been applied). We characterize the Markov property of the model, and propose a provably sound algorithm to identify causal relations as well as selection mechanisms up to the equivalence class, from data with soft interventions and unknown targets. Through synthetic and real-world experiments, we demonstrate that our algorithm effectively identifies true causal relations despite the presence of selection bias.

Permutation-Based Rank Test in the Presence of Discretization and Application in Causal Discovery with Mixed Data

Recent advances have shown that statistical tests for the rank of cross-covariance matrices play an important role in causal discovery. These rank tests include partial correlation tests as special cases and provide further graphical information about latent variables. Existing rank tests typically assume that all the continuous variables can be perfectly measured, and yet, in practice many variables can only be measured after discretization. For example, in psychometric studies, the continuous level of certain personality dimensions of a person can only be measured after being discretized into order-preserving options such as disagree, neutral, and agree. Motivated by this, we propose Mixed data Permutation-based Rank Test (MPRT), which properly controls the statistical errors even when some or all variables are discretized. Theoretically, we establish the exchangeability and estimate the asymptotic null distribution by permutations; as a consequence, MPRT can effectively control the Type I error in the presence of discretization while previous methods cannot. Empirically, our method is validated by extensive experiments on synthetic data and real-world data to demonstrate its effectiveness as well as applicability in causal discovery.

Differentiable Causal Discovery For Latent Hierarchical Causal Models

Discovering causal structures with latent variables from observational data is a fundamental challenge in causal discovery. Existing methods often rely on constraint-based, iterative discrete searches, limiting their scalability to large numbers of variables. Moreover, these methods frequently assume linearity or invertibility, restricting their applicability to real-world scenarios. We present new theoretical results on the identifiability of nonlinear latent hierarchical causal models, relaxing previous assumptions in literature about the deterministic nature of latent variables and exogenous noise. Building on these insights, we develop a novel differentiable causal discovery algorithm that efficiently estimates the structure of such models. To the best of our knowledge, this is the first work to propose a differentiable causal discovery method for nonlinear latent hierarchical models. Our approach outperforms existing methods in both accuracy and scalability. We demonstrate its practical utility by learning interpretable hierarchical latent structures from high-dimensional image data and demonstrate its effectiveness on downstream tasks.

Revisiting Differentiable Structure Learning: Inconsistency of $\ell_1$ Penalty and Beyond

Recent advances in differentiable structure learning have framed the combinatorial problem of learning directed acyclic graphs as a continuous optimization problem. Various aspects, including data standardization, have been studied to identify factors that influence the empirical performance of these methods. In this work, we investigate critical limitations in differentiable structure learning methods, focusing on settings where the true structure can be identified up to Markov equivalence classes, particularly in the linear Gaussian case. While Ng et al. (2024) highlighted potential non-convexity issues in this setting, we demonstrate and explain why the use of $\ell_1$-penalized likelihood in such cases is fundamentally inconsistent, even if the global optimum of the optimization problem can be found. To resolve this limitation, we develop a hybrid differentiable structure learning method based on $\ell_0$-penalized likelihood with hard acyclicity constraint, where the $\ell_0$ penalty can be approximated by different techniques including Gumbel-Softmax. Specifically, we first estimate the underlying moral graph, and use it to restrict the search space of the optimization problem, which helps alleviate the non-convexity issue. Experimental results show that the proposed method enhances empirical performance both before and after data standardization, providing a more reliable path for future advancements in differentiable structure learning, especially for learning Markov equivalence classes.

A Skewness-Based Criterion for Addressing Heteroscedastic Noise in Causal Discovery

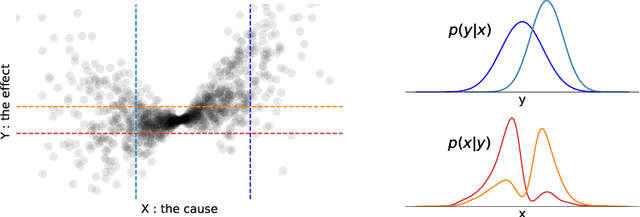
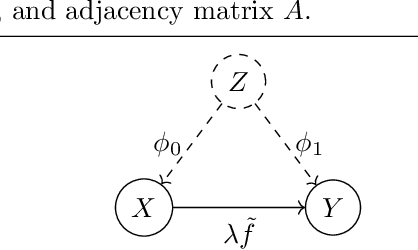
Real-world data often violates the equal-variance assumption (homoscedasticity), making it essential to account for heteroscedastic noise in causal discovery. In this work, we explore heteroscedastic symmetric noise models (HSNMs), where the effect $Y$ is modeled as $Y = f(X) + \sigma(X)N$, with $X$ as the cause and $N$ as independent noise following a symmetric distribution. We introduce a novel criterion for identifying HSNMs based on the skewness of the score (i.e., the gradient of the log density) of the data distribution. This criterion establishes a computationally tractable measurement that is zero in the causal direction but nonzero in the anticausal direction, enabling the causal direction discovery. We extend this skewness-based criterion to the multivariate setting and propose SkewScore, an algorithm that handles heteroscedastic noise without requiring the extraction of exogenous noise. We also conduct a case study on the robustness of SkewScore in a bivariate model with a latent confounder, providing theoretical insights into its performance. Empirical studies further validate the effectiveness of the proposed method.

On the Identifiability of Sparse ICA without Assuming Non-Gaussianity

Independent component analysis (ICA) is a fundamental statistical tool used to reveal hidden generative processes from observed data. However, traditional ICA approaches struggle with the rotational invariance inherent in Gaussian distributions, often necessitating the assumption of non-Gaussianity in the underlying sources. This may limit their applicability in broader contexts. To accommodate Gaussian sources, we develop an identifiability theory that relies on second-order statistics without imposing further preconditions on the distribution of sources, by introducing novel assumptions on the connective structure from sources to observed variables. Different from recent work that focuses on potentially restrictive connective structures, our proposed assumption of structural variability is both considerably less restrictive and provably necessary. Furthermore, we propose two estimation methods based on second-order statistics and sparsity constraint. Experimental results are provided to validate our identifiability theory and estimation methods.