Permutation-Based Rank Test in the Presence of Discretization and Application in Causal Discovery with Mixed Data

Recent advances have shown that statistical tests for the rank of cross-covariance matrices play an important role in causal discovery. These rank tests include partial correlation tests as special cases and provide further graphical information about latent variables. Existing rank tests typically assume that all the continuous variables can be perfectly measured, and yet, in practice many variables can only be measured after discretization. For example, in psychometric studies, the continuous level of certain personality dimensions of a person can only be measured after being discretized into order-preserving options such as disagree, neutral, and agree. Motivated by this, we propose Mixed data Permutation-based Rank Test (MPRT), which properly controls the statistical errors even when some or all variables are discretized. Theoretically, we establish the exchangeability and estimate the asymptotic null distribution by permutations; as a consequence, MPRT can effectively control the Type I error in the presence of discretization while previous methods cannot. Empirically, our method is validated by extensive experiments on synthetic data and real-world data to demonstrate its effectiveness as well as applicability in causal discovery.

On the Recoverability of Causal Relations from Temporally Aggregated I.I.D. Data

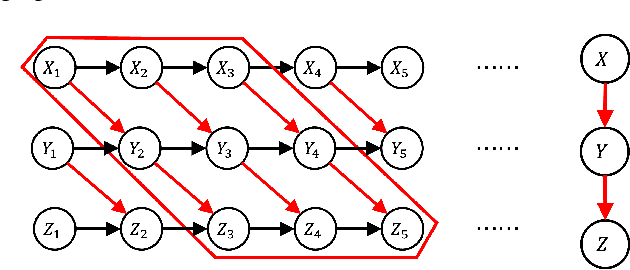
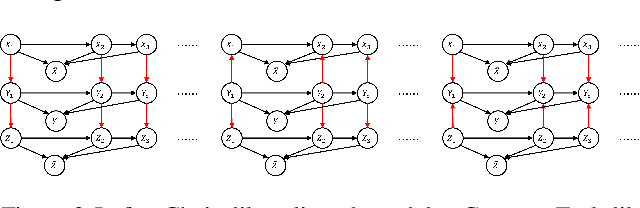
We consider the effect of temporal aggregation on instantaneous (non-temporal) causal discovery in general setting. This is motivated by the observation that the true causal time lag is often considerably shorter than the observational interval. This discrepancy leads to high aggregation, causing time-delay causality to vanish and instantaneous dependence to manifest. Although we expect such instantaneous dependence has consistency with the true causal relation in certain sense to make the discovery results meaningful, it remains unclear what type of consistency we need and when will such consistency be satisfied. We proposed functional consistency and conditional independence consistency in formal way correspond functional causal model-based methods and conditional independence-based methods respectively and provide the conditions under which these consistencies will hold. We show theoretically and experimentally that causal discovery results may be seriously distorted by aggregation especially in complete nonlinear case and we also find causal relationship still recoverable from aggregated data if we have partial linearity or appropriate prior. Our findings suggest community should take a cautious and meticulous approach when interpreting causal discovery results from such data and show why and when aggregation will distort the performance of causal discovery methods.

Unsupervised Sampling Promoting for Stochastic Human Trajectory Prediction

The indeterminate nature of human motion requires trajectory prediction systems to use a probabilistic model to formulate the multi-modality phenomenon and infer a finite set of future trajectories. However, the inference processes of most existing methods rely on Monte Carlo random sampling, which is insufficient to cover the realistic paths with finite samples, due to the long tail effect of the predicted distribution. To promote the sampling process of stochastic prediction, we propose a novel method, called BOsampler, to adaptively mine potential paths with Bayesian optimization in an unsupervised manner, as a sequential design strategy in which new prediction is dependent on the previously drawn samples. Specifically, we model the trajectory sampling as a Gaussian process and construct an acquisition function to measure the potential sampling value. This acquisition function applies the original distribution as prior and encourages exploring paths in the long-tail region. This sampling method can be integrated with existing stochastic predictive models without retraining. Experimental results on various baseline methods demonstrate the effectiveness of our method.