Type Information-Assisted Self-Supervised Knowledge Graph Denoising

Knowledge graphs serve as critical resources supporting intelligent systems, but they can be noisy due to imperfect automatic generation processes. Existing approaches to noise detection often rely on external facts, logical rule constraints, or structural embeddings. These methods are often challenged by imperfect entity alignment, flexible knowledge graph construction, and overfitting on structures. In this paper, we propose to exploit the consistency between entity and relation type information for noise detection, resulting a novel self-supervised knowledge graph denoising method that avoids those problems. We formalize type inconsistency noise as triples that deviate from the majority with respect to type-dependent reasoning along the topological structure. Specifically, we first extract a compact representation of a given knowledge graph via an encoder that models the type dependencies of triples. Then, the decoder reconstructs the original input knowledge graph based on the compact representation. It is worth noting that, our proposal has the potential to address the problems of knowledge graph compression and completion, although this is not our focus. For the specific task of noise detection, the discrepancy between the reconstruction results and the input knowledge graph provides an opportunity for denoising, which is facilitated by the type consistency embedded in our method. Experimental validation demonstrates the effectiveness of our approach in detecting potential noise in real-world data.

Practical Marketplace Optimization at Uber Using Causally-Informed Machine Learning

Budget allocation of marketplace levers, such as incentives for drivers and promotions for riders, has long been a technical and business challenge at Uber; understanding lever budget changes' impact and estimating cost efficiency to achieve predefined budgets is crucial, with the goal of optimal allocations that maximize business value; we introduce an end-to-end machine learning and optimization procedure to automate budget decision-making for cities, relying on feature store, model training and serving, optimizers, and backtesting; proposing state-of-the-art deep learning (DL) estimator based on S-Learner and a novel tensor B-Spline regression model, we solve high-dimensional optimization with ADMM and primal-dual interior point convex optimization, substantially improving Uber's resource allocation efficiency.

MuGSI: Distilling GNNs with Multi-Granularity Structural Information for Graph Classification

Recent works have introduced GNN-to-MLP knowledge distillation (KD) frameworks to combine both GNN's superior performance and MLP's fast inference speed. However, existing KD frameworks are primarily designed for node classification within single graphs, leaving their applicability to graph classification largely unexplored. Two main challenges arise when extending KD for node classification to graph classification: (1) The inherent sparsity of learning signals due to soft labels being generated at the graph level; (2) The limited expressiveness of student MLPs, especially in datasets with limited input feature spaces. To overcome these challenges, we introduce MuGSI, a novel KD framework that employs Multi-granularity Structural Information for graph classification. Specifically, we propose multi-granularity distillation loss in MuGSI to tackle the first challenge. This loss function is composed of three distinct components: graph-level distillation, subgraph-level distillation, and node-level distillation. Each component targets a specific granularity of the graph structure, ensuring a comprehensive transfer of structural knowledge from the teacher model to the student model. To tackle the second challenge, MuGSI proposes to incorporate a node feature augmentation component, thereby enhancing the expressiveness of the student MLPs and making them more capable learners. We perform extensive experiments across a variety of datasets and different teacher/student model architectures. The experiment results demonstrate the effectiveness, efficiency, and robustness of MuGSI. Codes are publicly available at: \textbf{\url{https://github.com/tianyao-aka/MuGSI}.}

Progressive Knowledge Graph Completion

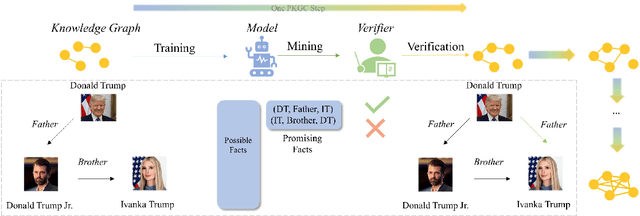
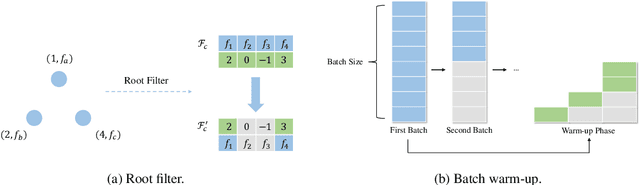
Knowledge Graph Completion (KGC) has emerged as a promising solution to address the issue of incompleteness within Knowledge Graphs (KGs). Traditional KGC research primarily centers on triple classification and link prediction. Nevertheless, we contend that these tasks do not align well with real-world scenarios and merely serve as surrogate benchmarks. In this paper, we investigate three crucial processes relevant to real-world construction scenarios: (a) the verification process, which arises from the necessity and limitations of human verifiers; (b) the mining process, which identifies the most promising candidates for verification; and (c) the training process, which harnesses verified data for subsequent utilization; in order to achieve a transition toward more realistic challenges. By integrating these three processes, we introduce the Progressive Knowledge Graph Completion (PKGC) task, which simulates the gradual completion of KGs in real-world scenarios. Furthermore, to expedite PKGC processing, we propose two acceleration modules: Optimized Top-$k$ algorithm and Semantic Validity Filter. These modules significantly enhance the efficiency of the mining procedure. Our experiments demonstrate that performance in link prediction does not accurately reflect performance in PKGC. A more in-depth analysis reveals the key factors influencing the results and provides potential directions for future research.

Prior Bilinear Based Models for Knowledge Graph Completion

Bilinear based models are powerful and widely used approaches for Knowledge Graphs Completion (KGC). Although bilinear based models have achieved significant advances, these studies mainly concentrate on posterior properties (based on evidence, e.g. symmetry pattern) while neglecting the prior properties. In this paper, we find a prior property named "the law of identity" that cannot be captured by bilinear based models, which hinders them from comprehensively modeling the characteristics of KGs. To address this issue, we introduce a solution called Unit Ball Bilinear Model (UniBi). This model not only achieves theoretical superiority but also offers enhanced interpretability and performance by minimizing ineffective learning through minimal constraints. Experiments demonstrate that UniBi models the prior property and verify its interpretability and performance.

D2Match: Leveraging Deep Learning and Degeneracy for Subgraph Matching

Subgraph matching is a fundamental building block for graph-based applications and is challenging due to its high-order combinatorial nature. Existing studies usually tackle it by combinatorial optimization or learning-based methods. However, they suffer from exponential computational costs or searching the matching without theoretical guarantees. In this paper, we develop D2Match by leveraging the efficiency of Deep learning and Degeneracy for subgraph matching. More specifically, we first prove that subgraph matching can degenerate to subtree matching, and subsequently is equivalent to finding a perfect matching on a bipartite graph. We can then yield an implementation of linear time complexity by the built-in tree-structured aggregation mechanism on graph neural networks. Moreover, circle structures and node attributes can be easily incorporated in D2Match to boost the matching performance. Finally, we conduct extensive experiments to show the superior performance of our D2Match and confirm that our D2Match indeed exploits the subtrees and differs from existing GNNs-based subgraph matching methods that depend on memorizing the data distribution divergence

Do Not Train It: A Linear Neural Architecture Search of Graph Neural Networks

Neural architecture search (NAS) for Graph neural networks (GNNs), called NAS-GNNs, has achieved significant performance over manually designed GNN architectures. However, these methods inherit issues from the conventional NAS methods, such as high computational cost and optimization difficulty. More importantly, previous NAS methods have ignored the uniqueness of GNNs, where GNNs possess expressive power without training. With the randomly-initialized weights, we can then seek the optimal architecture parameters via the sparse coding objective and derive a novel NAS-GNNs method, namely neural architecture coding (NAC). Consequently, our NAC holds a no-update scheme on GNNs and can efficiently compute in linear time. Empirical evaluations on multiple GNN benchmark datasets demonstrate that our approach leads to state-of-the-art performance, which is up to $200\times$ faster and $18.8\%$ more accurate than the strong baselines.

Feature Expansion for Graph Neural Networks

Graph neural networks aim to learn representations for graph-structured data and show impressive performance, particularly in node classification. Recently, many methods have studied the representations of GNNs from the perspective of optimization goals and spectral graph theory. However, the feature space that dominates representation learning has not been systematically studied in graph neural networks. In this paper, we propose to fill this gap by analyzing the feature space of both spatial and spectral models. We decompose graph neural networks into determined feature spaces and trainable weights, providing the convenience of studying the feature space explicitly using matrix space analysis. In particular, we theoretically find that the feature space tends to be linearly correlated due to repeated aggregations. Motivated by these findings, we propose 1) feature subspaces flattening and 2) structural principal components to expand the feature space. Extensive experiments verify the effectiveness of our proposed more comprehensive feature space, with comparable inference time to the baseline, and demonstrate its efficient convergence capability.

Improving Your Graph Neural Networks: A High-Frequency Booster

Graph neural networks (GNNs) hold the promise of learning efficient representations of graph-structured data, and one of its most important applications is semi-supervised node classification. However, in this application, GNN frameworks tend to fail due to the following issues: over-smoothing and heterophily. The most popular GNNs are known to be focused on the message-passing framework, and recent research shows that these GNNs are often bounded by low-pass filters from a signal processing perspective. We thus incorporate high-frequency information into GNNs to alleviate this genetic problem. In this paper, we argue that the complement of the original graph incorporates a high-pass filter and propose Complement Laplacian Regularization (CLAR) for an efficient enhancement of high-frequency components. The experimental results demonstrate that CLAR helps GNNs tackle over-smoothing, improving the expressiveness of heterophilic graphs, which adds up to 3.6% improvement over popular baselines and ensures topological robustness.