Empowering Graph Invariance Learning with Deep Spurious Infomax

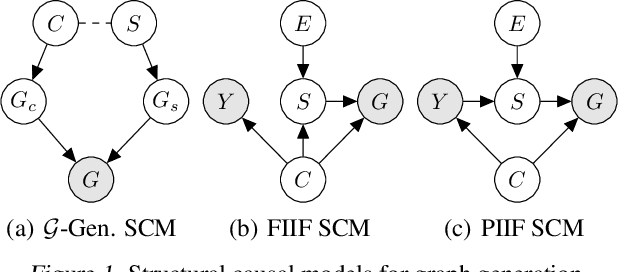
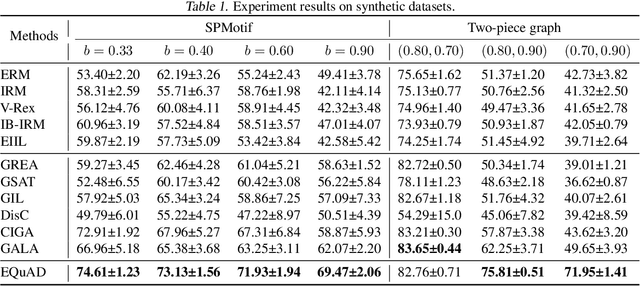
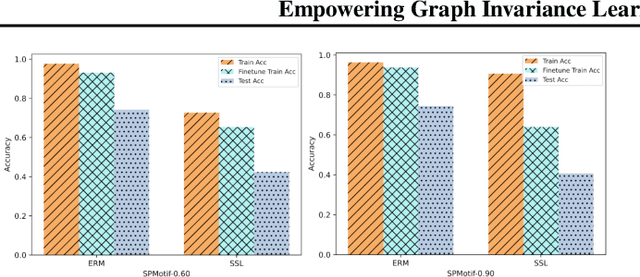
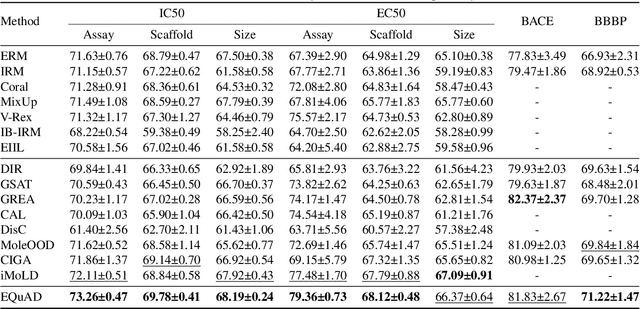
Recently, there has been a surge of interest in developing graph neural networks that utilize the invariance principle on graphs to generalize the out-of-distribution (OOD) data. Due to the limited knowledge about OOD data, existing approaches often pose assumptions about the correlation strengths of the underlying spurious features and the target labels. However, this prior is often unavailable and will change arbitrarily in the real-world scenarios, which may lead to severe failures of the existing graph invariance learning methods. To bridge this gap, we introduce a novel graph invariance learning paradigm, which induces a robust and general inductive bias. The paradigm is built upon the observation that the infomax principle encourages learning spurious features regardless of spurious correlation strengths. We further propose the EQuAD framework that realizes this learning paradigm and employs tailored learning objectives that provably elicit invariant features by disentangling them from the spurious features learned through infomax. Notably, EQuAD shows stable and enhanced performance across different degrees of bias in synthetic datasets and challenging real-world datasets up to $31.76\%$. Our code is available at \url{https://github.com/tianyao-aka/EQuAD}.

MuGSI: Distilling GNNs with Multi-Granularity Structural Information for Graph Classification

Recent works have introduced GNN-to-MLP knowledge distillation (KD) frameworks to combine both GNN's superior performance and MLP's fast inference speed. However, existing KD frameworks are primarily designed for node classification within single graphs, leaving their applicability to graph classification largely unexplored. Two main challenges arise when extending KD for node classification to graph classification: (1) The inherent sparsity of learning signals due to soft labels being generated at the graph level; (2) The limited expressiveness of student MLPs, especially in datasets with limited input feature spaces. To overcome these challenges, we introduce MuGSI, a novel KD framework that employs Multi-granularity Structural Information for graph classification. Specifically, we propose multi-granularity distillation loss in MuGSI to tackle the first challenge. This loss function is composed of three distinct components: graph-level distillation, subgraph-level distillation, and node-level distillation. Each component targets a specific granularity of the graph structure, ensuring a comprehensive transfer of structural knowledge from the teacher model to the student model. To tackle the second challenge, MuGSI proposes to incorporate a node feature augmentation component, thereby enhancing the expressiveness of the student MLPs and making them more capable learners. We perform extensive experiments across a variety of datasets and different teacher/student model architectures. The experiment results demonstrate the effectiveness, efficiency, and robustness of MuGSI. Codes are publicly available at: \textbf{\url{https://github.com/tianyao-aka/MuGSI}.}

Improving the Expressiveness of $K$-hop Message-Passing GNNs by Injecting Contextualized Substructure Information

Graph neural networks (GNNs) have become the \textit{de facto} standard for representational learning in graphs, and have achieved state-of-the-art performance in many graph-related tasks; however, it has been shown that the expressive power of standard GNNs are equivalent maximally to 1-dimensional Weisfeiler-Lehman (1-WL) Test. Recently, there is a line of works aiming to enhance the expressive power of graph neural networks. One line of such works aim at developing $K$-hop message-passing GNNs where node representation is updated by aggregating information from not only direct neighbors but all neighbors within $K$-hop of the node. Another line of works leverages subgraph information to enhance the expressive power which is proven to be strictly more powerful than 1-WL test. In this work, we discuss the limitation of $K$-hop message-passing GNNs and propose \textit{substructure encoding function} to uplift the expressive power of any $K$-hop message-passing GNN. We further inject contextualized substructure information to enhance the expressiveness of $K$-hop message-passing GNNs. Our method is provably more powerful than previous works on $K$-hop graph neural networks and 1-WL subgraph GNNs, which is a specific type of subgraph based GNN models, and not less powerful than 3-WL. Empirically, our proposed method set new state-of-the-art performance or achieves comparable performance for a variety of datasets. Our code is available at \url{https://github.com/tianyao-aka/Expresive_K_hop_GNNs}.

Efficient LLM Jailbreak via Adaptive Dense-to-sparse Constrained Optimization

Recent research indicates that large language models (LLMs) are susceptible to jailbreaking attacks that can generate harmful content. This paper introduces a novel token-level attack method, Adaptive Dense-to-Sparse Constrained Optimization (ADC), which effectively jailbreaks several open-source LLMs. Our approach relaxes the discrete jailbreak optimization into a continuous optimization and progressively increases the sparsity of the optimizing vectors. Consequently, our method effectively bridges the gap between discrete and continuous space optimization. Experimental results demonstrate that our method is more effective and efficient than existing token-level methods. On Harmbench, our method achieves state of the art attack success rate on seven out of eight LLMs. Code will be made available. Trigger Warning: This paper contains model behavior that can be offensive in nature.