Natural Counterfactuals With Necessary Backtracking

Counterfactual reasoning is pivotal in human cognition and especially important for providing explanations and making decisions. While Judea Pearl's influential approach is theoretically elegant, its generation of a counterfactual scenario often requires interventions that are too detached from the real scenarios to be feasible. In response, we propose a framework of natural counterfactuals and a method for generating counterfactuals that are natural with respect to the actual world's data distribution. Our methodology refines counterfactual reasoning, allowing changes in causally preceding variables to minimize deviations from realistic scenarios. To generate natural counterfactuals, we introduce an innovative optimization framework that permits but controls the extent of backtracking with a naturalness criterion. Empirical experiments indicate the effectiveness of our method.

Reframed GES with a Neural Conditional Dependence Measure

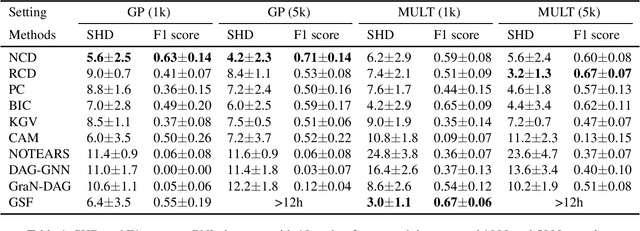
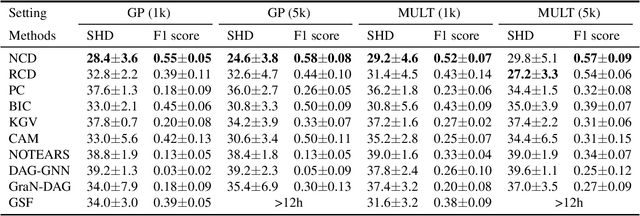
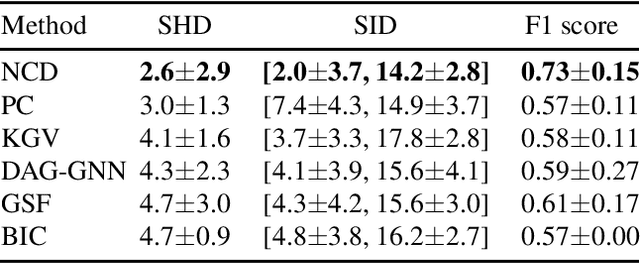
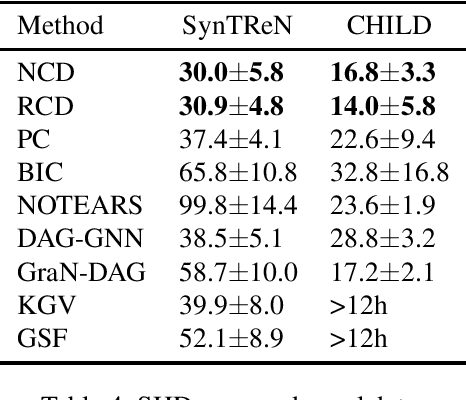
In a nonparametric setting, the causal structure is often identifiable only up to Markov equivalence, and for the purpose of causal inference, it is useful to learn a graphical representation of the Markov equivalence class (MEC). In this paper, we revisit the Greedy Equivalence Search (GES) algorithm, which is widely cited as a score-based algorithm for learning the MEC of the underlying causal structure. We observe that in order to make the GES algorithm consistent in a nonparametric setting, it is not necessary to design a scoring metric that evaluates graphs. Instead, it suffices to plug in a consistent estimator of a measure of conditional dependence to guide the search. We therefore present a reframing of the GES algorithm, which is more flexible than the standard score-based version and readily lends itself to the nonparametric setting with a general measure of conditional dependence. In addition, we propose a neural conditional dependence (NCD) measure, which utilizes the expressive power of deep neural networks to characterize conditional independence in a nonparametric manner. We establish the optimality of the reframed GES algorithm under standard assumptions and the consistency of using our NCD estimator to decide conditional independence. Together these results justify the proposed approach. Experimental results demonstrate the effectiveness of our method in causal discovery, as well as the advantages of using our NCD measure over kernel-based measures.

What-Is and How-To for Fairness in Machine Learning: A Survey, Reflection, and Perspective

Algorithmic fairness has attracted increasing attention in the machine learning community. Various definitions are proposed in the literature, but the differences and connections among them are not clearly addressed. In this paper, we review and reflect on various fairness notions previously proposed in machine learning literature, and make an attempt to draw connections to arguments in moral and political philosophy, especially theories of justice. We also consider fairness inquiries from a dynamic perspective, and further consider the long-term impact that is induced by current prediction and decision. In light of the differences in the characterized fairness, we present a flowchart that encompasses implicit assumptions and expected outcomes of different types of fairness inquiries on the data generating process, on the predicted outcome, and on the induced impact, respectively. This paper demonstrates the importance of matching the mission (which kind of fairness one would like to enforce) and the means (which spectrum of fairness analysis is of interest, what is the appropriate analyzing scheme) to fulfill the intended purpose.

Markov categories, causal theories, and the do-calculus

We give a category-theoretic treatment of causal models that formalizes the syntax for causal reasoning over a directed acyclic graph (DAG) by associating a free Markov category with the DAG in a canonical way. This framework enables us to define and study important concepts in causal reasoning from an abstract and "purely causal" point of view, such as causal independence/separation, causal conditionals, and decomposition of intervention effects. Our results regarding these concepts abstract away from the details of the commonly adopted causal models such as (recursive) structural equation models or causal Bayesian networks. They are therefore more widely applicable and in a way conceptually clearer. Our results are also intimately related to Judea Pearl's celebrated do-calculus, and yield a syntactic version of a core part of the calculus that is inherited in all causal models. In particular, it induces a simpler and specialized version of Pearl's do-calculus in the context of causal Bayesian networks, which we show is as strong as the full version.

Reliable Causal Discovery with Improved Exact Search and Weaker Assumptions

Many of the causal discovery methods rely on the faithfulness assumption to guarantee asymptotic correctness. However, the assumption can be approximately violated in many ways, leading to sub-optimal solutions. Although there is a line of research in Bayesian network structure learning that focuses on weakening the assumption, such as exact search methods with well-defined score functions, they do not scale well to large graphs. In this work, we introduce several strategies to improve the scalability of exact score-based methods in the linear Gaussian setting. In particular, we develop a super-structure estimation method based on the support of inverse covariance matrix which requires assumptions that are strictly weaker than faithfulness, and apply it to restrict the search space of exact search. We also propose a local search strategy that performs exact search on the local clusters formed by each variable and its neighbors within two hops in the super-structure. Numerical experiments validate the efficacy of the proposed procedure, and demonstrate that it scales up to hundreds of nodes with a high accuracy.

Ancestral instrument method for causal inference without a causal graph

Unobserved confounding is the main obstacle to causal effect estimation from observational data. Instrumental variables (IVs) are widely used for causal effect estimation when there exist latent confounders. With the standard IV method, when a given IV is valid, unbiased estimation can be obtained, but the validity requirement of standard IV is strict and untestable. Conditional IV has been proposed to relax the requirement of standard IV by conditioning on a set of observed variables (known as a conditioning set for a conditional IV). However, the criterion for finding a conditioning set for a conditional IV needs complete causal structure knowledge or a directed acyclic graph (DAG) representing the causal relationships of both observed and unobserved variables. This makes it impossible to discover a conditioning set directly from data. In this paper, by leveraging maximal ancestral graphs (MAGs) in causal inference with latent variables, we propose a new type of IV, ancestral IV in MAG, and develop the theory to support data-driven discovery of the conditioning set for a given ancestral IV in MAG. Based on the theory, we develop an algorithm for unbiased causal effect estimation with an ancestral IV in MAG and observational data. Extensive experiments on synthetic and real-world datasets have demonstrated the performance of the algorithm in comparison with existing IV methods.

Low Rank Directed Acyclic Graphs and Causal Structure Learning

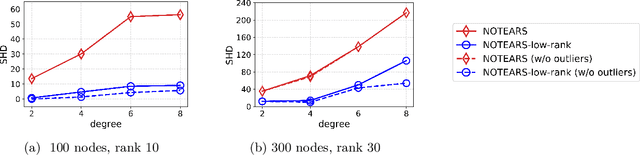
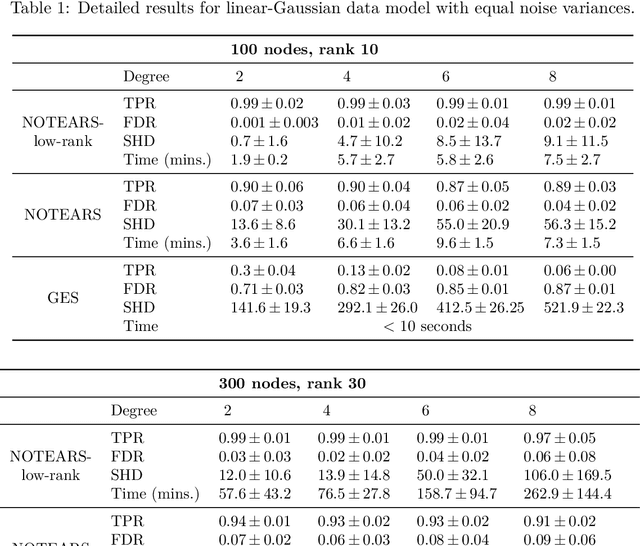
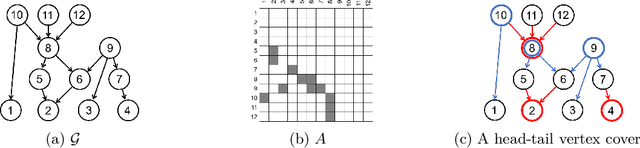
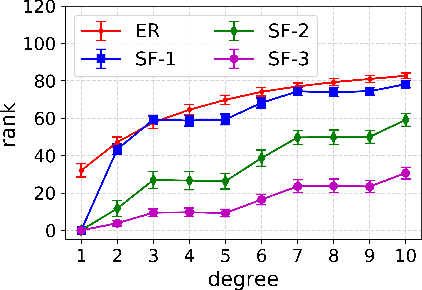
Despite several important advances in recent years, learning causal structures represented by directed acyclic graphs (DAGs) remains a challenging task in high dimensional settings when the graphs to be learned are not sparse. In particular, the recent formulation of structure learning as a continuous optimization problem proved to have considerable advantages over the traditional combinatorial formulation, but the performance of the resulting algorithms is still wanting when the target graph is relatively large and dense. In this paper we propose a novel approach to mitigate this problem, by exploiting a low rank assumption regarding the (weighted) adjacency matrix of a DAG causal model. We establish several useful results relating interpretable graphical conditions to the low rank assumption, and show how to adapt existing methods for causal structure learning to take advantage of this assumption. We also provide empirical evidence for the utility of our low rank algorithms, especially on graphs that are not sparse. Not only do they outperform state-of-the-art algorithms when the low rank condition is satisfied, the performance on randomly generated scale-free graphs is also very competitive even though the true ranks may not be as low as is assumed.

ASP-based Discovery of Semi-Markovian Causal Models under Weaker Assumptions

In recent years the possibility of relaxing the so-called Faithfulness assumption in automated causal discovery has been investigated. The investigation showed (1) that the Faithfulness assumption can be weakened in various ways that in an important sense preserve its power, and (2) that weakening of Faithfulness may help to speed up methods based on Answer Set Programming. However, this line of work has so far only considered the discovery of causal models without latent variables. In this paper, we study weakenings of Faithfulness for constraint-based discovery of semi-Markovian causal models, which accommodate the possibility of latent variables, and show that both (1) and (2) remain the case in this more realistic setting.

Causal Discovery from Heterogeneous/Nonstationary Data

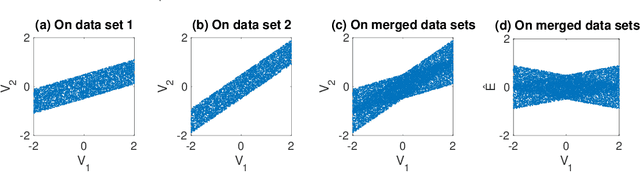
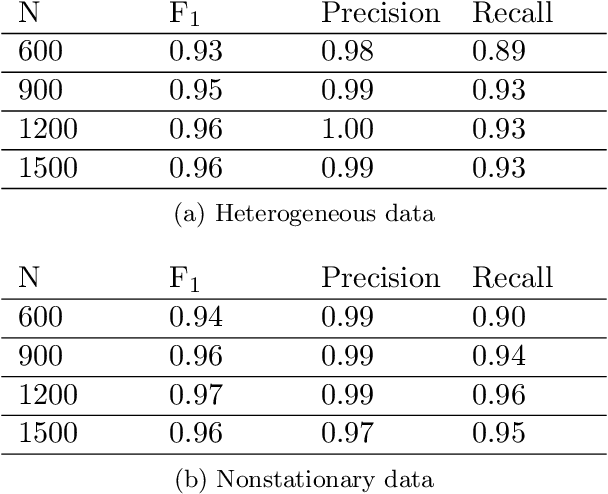
It is commonplace to encounter heterogeneous or nonstationary data, of which the underlying generating process changes across domains or over time. Such a distribution shift feature presents both challenges and opportunities for causal discovery. In this paper, we develop a framework for causal discovery from such data, called Constraint-based causal Discovery from heterogeneous/NOnstationary Data (CD-NOD), to find causal skeleton and directions and estimate the properties of mechanism changes. First, we propose an enhanced constraint-based procedure to detect variables whose local mechanisms change and recover the skeleton of the causal structure over observed variables. Second, we present a method to determine causal orientations by making use of independent changes in the data distribution implied by the underlying causal model, benefiting from information carried by changing distributions. After learning the causal structure, next, we investigate how to efficiently estimate the `driving force' of the nonstationarity of a causal mechanism. That is, we aim to extract from data a low-dimensional representation of changes. The proposed methods are nonparametric, with no hard restrictions on data distributions and causal mechanisms, and do not rely on window segmentation. Furthermore, we find that data heterogeneity benefits causal structure identification even with particular types of confounders. Finally, we show the connection between heterogeneity/nonstationarity and soft intervention in causal discovery. Experimental results on various synthetic and real-world data sets (task-fMRI and stock market data) are presented to demonstrate the efficacy of the proposed methods.

Causal Identification under Markov Equivalence

Assessing the magnitude of cause-and-effect relations is one of the central challenges found throughout the empirical sciences. The problem of identification of causal effects is concerned with determining whether a causal effect can be computed from a combination of observational data and substantive knowledge about the domain under investigation, which is formally expressed in the form of a causal graph. In many practical settings, however, the knowledge available for the researcher is not strong enough so as to specify a unique causal graph. Another line of investigation attempts to use observational data to learn a qualitative description of the domain called a Markov equivalence class, which is the collection of causal graphs that share the same set of observed features. In this paper, we marry both approaches and study the problem of causal identification from an equivalence class, represented by a partial ancestral graph (PAG). We start by deriving a set of graphical properties of PAGs that are carried over to its induced subgraphs. We then develop an algorithm to compute the effect of an arbitrary set of variables on an arbitrary outcome set. We show that the algorithm is strictly more powerful than the current state of the art found in the literature.