Leaning Time-Varying Instruments for Identifying Causal Effects in Time-Series Data

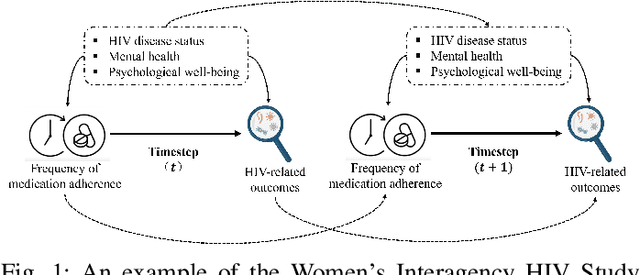
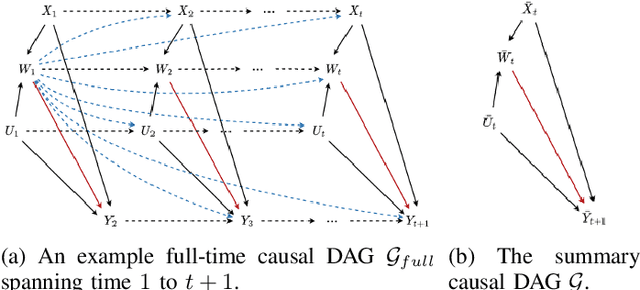
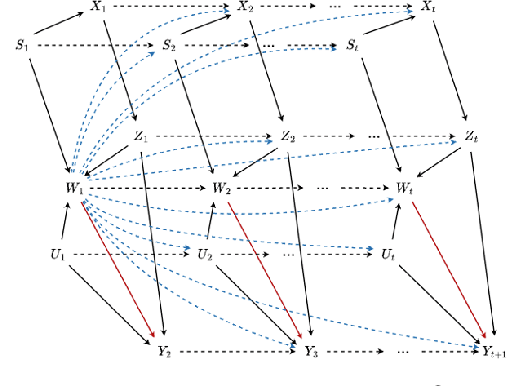
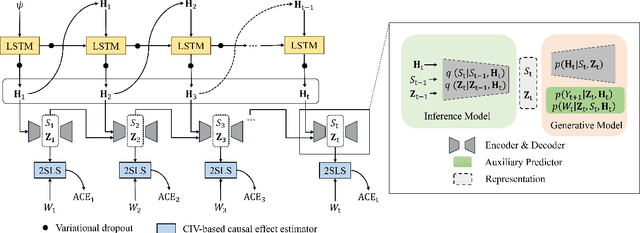
Querying causal effects from time-series data is important across various fields, including healthcare, economics, climate science, and epidemiology. However, this task becomes complex in the existence of time-varying latent confounders, which affect both treatment and outcome variables over time and can introduce bias in causal effect estimation. Traditional instrumental variable (IV) methods are limited in addressing such complexities due to the need for predefined IVs or strong assumptions that do not hold in dynamic settings. To tackle these issues, we develop a novel Time-varying Conditional Instrumental Variables (CIV) for Debiasing causal effect estimation, referred to as TDCIV. TDCIV leverages Long Short-Term Memory (LSTM) and Variational Autoencoder (VAE) models to disentangle and learn the representations of time-varying CIV and its conditioning set from proxy variables without prior knowledge. Under the assumptions of the Markov property and availability of proxy variables, we theoretically establish the validity of these learned representations for addressing the biases from time-varying latent confounders, thus enabling accurate causal effect estimation. Our proposed TDCIV is the first to effectively learn time-varying CIV and its associated conditioning set without relying on domain-specific knowledge.

Ancestral instrument method for causal inference without a causal graph

Unobserved confounding is the main obstacle to causal effect estimation from observational data. Instrumental variables (IVs) are widely used for causal effect estimation when there exist latent confounders. With the standard IV method, when a given IV is valid, unbiased estimation can be obtained, but the validity requirement of standard IV is strict and untestable. Conditional IV has been proposed to relax the requirement of standard IV by conditioning on a set of observed variables (known as a conditioning set for a conditional IV). However, the criterion for finding a conditioning set for a conditional IV needs complete causal structure knowledge or a directed acyclic graph (DAG) representing the causal relationships of both observed and unobserved variables. This makes it impossible to discover a conditioning set directly from data. In this paper, by leveraging maximal ancestral graphs (MAGs) in causal inference with latent variables, we propose a new type of IV, ancestral IV in MAG, and develop the theory to support data-driven discovery of the conditioning set for a given ancestral IV in MAG. Based on the theory, we develop an algorithm for unbiased causal effect estimation with an ancestral IV in MAG and observational data. Extensive experiments on synthetic and real-world datasets have demonstrated the performance of the algorithm in comparison with existing IV methods.