Unbiased Reasoning for Knowledge-Intensive Tasks in Large Language Models via Conditional Front-Door Adjustment

Large Language Models (LLMs) have shown impressive capabilities in natural language processing but still struggle to perform well on knowledge-intensive tasks that require deep reasoning and the integration of external knowledge. Although methods such as Retrieval-Augmented Generation (RAG) and Chain-of-Thought (CoT) have been proposed to enhance LLMs with external knowledge, they still suffer from internal bias in LLMs, which often leads to incorrect answers. In this paper, we propose a novel causal prompting framework, Conditional Front-Door Prompting (CFD-Prompting), which enables the unbiased estimation of the causal effect between the query and the answer, conditional on external knowledge, while mitigating internal bias. By constructing counterfactual external knowledge, our framework simulates how the query behaves under varying contexts, addressing the challenge that the query is fixed and is not amenable to direct causal intervention. Compared to the standard front-door adjustment, the conditional variant operates under weaker assumptions, enhancing both robustness and generalisability of the reasoning process. Extensive experiments across multiple LLMs and benchmark datasets demonstrate that CFD-Prompting significantly outperforms existing baselines in both accuracy and robustness.

Revisiting Pre-processing Group Fairness: A Modular Benchmarking Framework

As machine learning systems become increasingly integrated into high-stakes decision-making processes, ensuring fairness in algorithmic outcomes has become a critical concern. Methods to mitigate bias typically fall into three categories: pre-processing, in-processing, and post-processing. While significant attention has been devoted to the latter two, pre-processing methods, which operate at the data level and offer advantages such as model-agnosticism and improved privacy compliance, have received comparatively less focus and lack standardised evaluation tools. In this work, we introduce FairPrep, an extensible and modular benchmarking framework designed to evaluate fairness-aware pre-processing techniques on tabular datasets. Built on the AIF360 platform, FairPrep allows seamless integration of datasets, fairness interventions, and predictive models. It features a batch-processing interface that enables efficient experimentation and automatic reporting of fairness and utility metrics. By offering standardised pipelines and supporting reproducible evaluations, FairPrep fills a critical gap in the fairness benchmarking landscape and provides a practical foundation for advancing data-level fairness research.

FairDRL-ST: Disentangled Representation Learning for Fair Spatio-Temporal Mobility Prediction

As deep spatio-temporal neural networks are increasingly utilised in urban computing contexts, the deployment of such methods can have a direct impact on users of critical urban infrastructure, such as public transport, emergency services, and traffic management systems. While many spatio-temporal methods focus on improving accuracy, fairness has recently gained attention due to growing evidence that biased predictions in spatio-temporal applications can disproportionately disadvantage certain demographic or geographic groups, thereby reinforcing existing socioeconomic inequalities and undermining the ethical deployment of AI in public services. In this paper, we propose a novel framework, FairDRL-ST, based on disentangled representation learning, to address fairness concerns in spatio-temporal prediction, with a particular focus on mobility demand forecasting. By leveraging adversarial learning and disentangled representation learning, our framework learns to separate attributes that contain sensitive information. Unlike existing methods that enforce fairness through supervised learning, which may lead to overcompensation and degraded performance, our framework achieves fairness in an unsupervised manner with minimal performance loss. We apply our framework to real-world urban mobility datasets and demonstrate its ability to close fairness gaps while delivering competitive predictive performance compared to state-of-the-art fairness-aware methods.

Cultural Bias Matters: A Cross-Cultural Benchmark Dataset and Sentiment-Enriched Model for Understanding Multimodal Metaphors

Metaphors are pervasive in communication, making them crucial for natural language processing (NLP). Previous research on automatic metaphor processing predominantly relies on training data consisting of English samples, which often reflect Western European or North American biases. This cultural skew can lead to an overestimation of model performance and contributions to NLP progress. However, the impact of cultural bias on metaphor processing, particularly in multimodal contexts, remains largely unexplored. To address this gap, we introduce MultiMM, a Multicultural Multimodal Metaphor dataset designed for cross-cultural studies of metaphor in Chinese and English. MultiMM consists of 8,461 text-image advertisement pairs, each accompanied by fine-grained annotations, providing a deeper understanding of multimodal metaphors beyond a single cultural domain. Additionally, we propose Sentiment-Enriched Metaphor Detection (SEMD), a baseline model that integrates sentiment embeddings to enhance metaphor comprehension across cultural backgrounds. Experimental results validate the effectiveness of SEMD on metaphor detection and sentiment analysis tasks. We hope this work increases awareness of cultural bias in NLP research and contributes to the development of fairer and more inclusive language models. Our dataset and code are available at https://github.com/DUTIR-YSQ/MultiMM.

PUB: An LLM-Enhanced Personality-Driven User Behaviour Simulator for Recommender System Evaluation

Traditional offline evaluation methods for recommender systems struggle to capture the complexity of modern platforms due to sparse behavioural signals, noisy data, and limited modelling of user personality traits. While simulation frameworks can generate synthetic data to address these gaps, existing methods fail to replicate behavioural diversity, limiting their effectiveness. To overcome these challenges, we propose the Personality-driven User Behaviour Simulator (PUB), an LLM-based simulation framework that integrates the Big Five personality traits to model personalised user behaviour. PUB dynamically infers user personality from behavioural logs (e.g., ratings, reviews) and item metadata, then generates synthetic interactions that preserve statistical fidelity to real-world data. Experiments on the Amazon review datasets show that logs generated by PUB closely align with real user behaviour and reveal meaningful associations between personality traits and recommendation outcomes. These results highlight the potential of the personality-driven simulator to advance recommender system evaluation, offering scalable, controllable, high-fidelity alternatives to resource-intensive real-world experiments.

Fairness in Graph Learning Augmented with Machine Learning: A Survey

Augmenting specialised machine learning techniques into traditional graph learning models has achieved notable success across various domains, including federated graph learning, dynamic graph learning, and graph transformers. However, the intricate mechanisms of these specialised techniques introduce significant challenges in maintaining model fairness, potentially resulting in discriminatory outcomes in high-stakes applications such as recommendation systems, disaster response, criminal justice, and loan approval. This paper systematically examines the unique fairness challenges posed by Graph Learning augmented with Machine Learning (GL-ML). It highlights the complex interplay between graph learning mechanisms and machine learning techniques, emphasising how the augmentation of machine learning both enhances and complicates fairness. Additionally, we explore four critical techniques frequently employed to improve fairness in GL-ML methods. By thoroughly investigating the root causes and broader implications of fairness challenges in this rapidly evolving field, this work establishes a robust foundation for future research and innovation in GL-ML fairness.

Leaning Time-Varying Instruments for Identifying Causal Effects in Time-Series Data

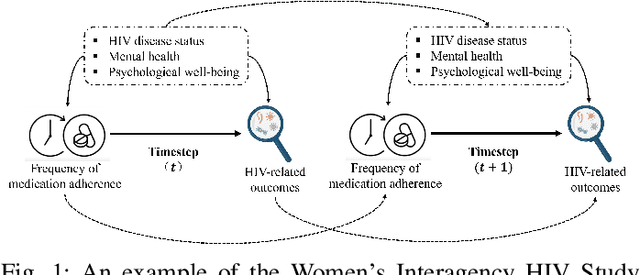
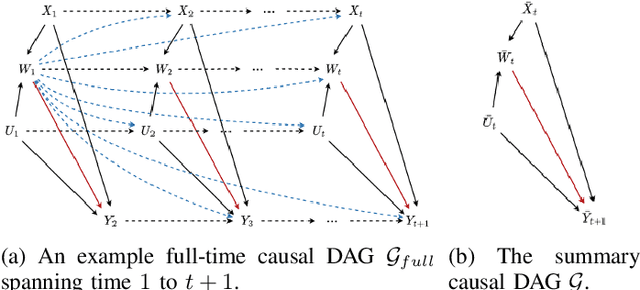
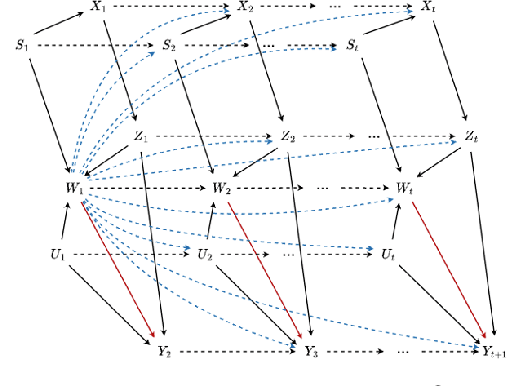
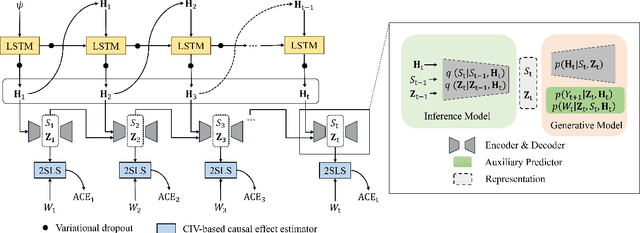
Querying causal effects from time-series data is important across various fields, including healthcare, economics, climate science, and epidemiology. However, this task becomes complex in the existence of time-varying latent confounders, which affect both treatment and outcome variables over time and can introduce bias in causal effect estimation. Traditional instrumental variable (IV) methods are limited in addressing such complexities due to the need for predefined IVs or strong assumptions that do not hold in dynamic settings. To tackle these issues, we develop a novel Time-varying Conditional Instrumental Variables (CIV) for Debiasing causal effect estimation, referred to as TDCIV. TDCIV leverages Long Short-Term Memory (LSTM) and Variational Autoencoder (VAE) models to disentangle and learn the representations of time-varying CIV and its conditioning set from proxy variables without prior knowledge. Under the assumptions of the Markov property and availability of proxy variables, we theoretically establish the validity of these learned representations for addressing the biases from time-varying latent confounders, thus enabling accurate causal effect estimation. Our proposed TDCIV is the first to effectively learn time-varying CIV and its associated conditioning set without relying on domain-specific knowledge.

Deconfounding Time Series Forecasting

Time series forecasting is a critical task in various domains, where accurate predictions can drive informed decision-making. Traditional forecasting methods often rely on current observations of variables to predict future outcomes, typically overlooking the influence of latent confounders, unobserved variables that simultaneously affect both the predictors and the target outcomes. This oversight can introduce bias and degrade the performance of predictive models. In this study, we address this challenge by proposing an enhanced forecasting approach that incorporates representations of latent confounders derived from historical data. By integrating these confounders into the predictive process, our method aims to improve the accuracy and robustness of time series forecasts. The proposed approach is demonstrated through its application to climate science data, showing significant improvements over traditional methods that do not account for confounders.

Linking Model Intervention to Causal Interpretation in Model Explanation

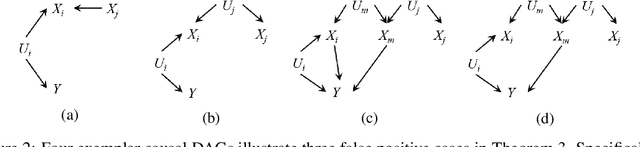
Intervention intuition is often used in model explanation where the intervention effect of a feature on the outcome is quantified by the difference of a model prediction when the feature value is changed from the current value to the baseline value. Such a model intervention effect of a feature is inherently association. In this paper, we will study the conditions when an intuitive model intervention effect has a causal interpretation, i.e., when it indicates whether a feature is a direct cause of the outcome. This work links the model intervention effect to the causal interpretation of a model. Such an interpretation capability is important since it indicates whether a machine learning model is trustworthy to domain experts. The conditions also reveal the limitations of using a model intervention effect for causal interpretation in an environment with unobserved features. Experiments on semi-synthetic datasets have been conducted to validate theorems and show the potential for using the model intervention effect for model interpretation.

TSI: A Multi-View Representation Learning Approach for Time Series Forecasting

As the growing demand for long sequence time-series forecasting in real-world applications, such as electricity consumption planning, the significance of time series forecasting becomes increasingly crucial across various domains. This is highlighted by recent advancements in representation learning within the field. This study introduces a novel multi-view approach for time series forecasting that innovatively integrates trend and seasonal representations with an Independent Component Analysis (ICA)-based representation. Recognizing the limitations of existing methods in representing complex and high-dimensional time series data, this research addresses the challenge by combining TS (trend and seasonality) and ICA (independent components) perspectives. This approach offers a holistic understanding of time series data, going beyond traditional models that often miss nuanced, nonlinear relationships. The efficacy of TSI model is demonstrated through comprehensive testing on various benchmark datasets, where it shows superior performance over current state-of-the-art models, particularly in multivariate forecasting. This method not only enhances the accuracy of forecasting but also contributes significantly to the field by providing a more in-depth understanding of time series data. The research which uses ICA for a view lays the groundwork for further exploration and methodological advancements in time series forecasting, opening new avenues for research and practical applications.