Linking Model Intervention to Causal Interpretation in Model Explanation

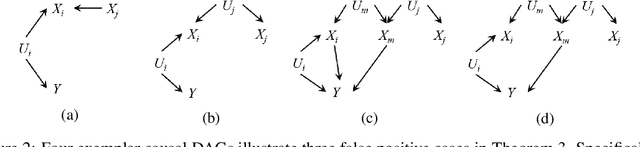
Intervention intuition is often used in model explanation where the intervention effect of a feature on the outcome is quantified by the difference of a model prediction when the feature value is changed from the current value to the baseline value. Such a model intervention effect of a feature is inherently association. In this paper, we will study the conditions when an intuitive model intervention effect has a causal interpretation, i.e., when it indicates whether a feature is a direct cause of the outcome. This work links the model intervention effect to the causal interpretation of a model. Such an interpretation capability is important since it indicates whether a machine learning model is trustworthy to domain experts. The conditions also reveal the limitations of using a model intervention effect for causal interpretation in an environment with unobserved features. Experiments on semi-synthetic datasets have been conducted to validate theorems and show the potential for using the model intervention effect for model interpretation.

TSI: A Multi-View Representation Learning Approach for Time Series Forecasting

As the growing demand for long sequence time-series forecasting in real-world applications, such as electricity consumption planning, the significance of time series forecasting becomes increasingly crucial across various domains. This is highlighted by recent advancements in representation learning within the field. This study introduces a novel multi-view approach for time series forecasting that innovatively integrates trend and seasonal representations with an Independent Component Analysis (ICA)-based representation. Recognizing the limitations of existing methods in representing complex and high-dimensional time series data, this research addresses the challenge by combining TS (trend and seasonality) and ICA (independent components) perspectives. This approach offers a holistic understanding of time series data, going beyond traditional models that often miss nuanced, nonlinear relationships. The efficacy of TSI model is demonstrated through comprehensive testing on various benchmark datasets, where it shows superior performance over current state-of-the-art models, particularly in multivariate forecasting. This method not only enhances the accuracy of forecasting but also contributes significantly to the field by providing a more in-depth understanding of time series data. The research which uses ICA for a view lays the groundwork for further exploration and methodological advancements in time series forecasting, opening new avenues for research and practical applications.

A Deconfounding Approach to Climate Model Bias Correction

Global Climate Models (GCMs) are crucial for predicting future climate changes by simulating the Earth systems. However, GCM outputs exhibit systematic biases due to model uncertainties, parameterization simplifications, and inadequate representation of complex climate phenomena. Traditional bias correction methods, which rely on historical observation data and statistical techniques, often neglect unobserved confounders, leading to biased results. This paper proposes a novel bias correction approach to utilize both GCM and observational data to learn a factor model that captures multi-cause latent confounders. Inspired by recent advances in causality based time series deconfounding, our method first constructs a factor model to learn latent confounders from historical data and then applies them to enhance the bias correction process using advanced time series forecasting models. The experimental results demonstrate significant improvements in the accuracy of precipitation outputs. By addressing unobserved confounders, our approach offers a robust and theoretically grounded solution for climate model bias correction.

A transformer boosted UNet for smoke segmentation in complex backgrounds in multispectral LandSat imagery

Many studies have been done to detect smokes from satellite imagery. However, these prior methods are not still effective in detecting various smokes in complex backgrounds. Smokes present challenges in detection due to variations in density, color, lighting, and backgrounds such as clouds, haze, and/or mist, as well as the contextual nature of thin smoke. This paper addresses these challenges by proposing a new segmentation model called VTrUNet which consists of a virtual band construction module to capture spectral patterns and a transformer boosted UNet to capture long range contextual features. The model takes imagery of six bands: red, green, blue, near infrared, and two shortwave infrared bands as input. To show the advantages of the proposed model, the paper presents extensive results for various possible model architectures improving UNet and draws interesting conclusions including that adding more modules to a model does not always lead to a better performance. The paper also compares the proposed model with very recently proposed and related models for smoke segmentation and shows that the proposed model performs the best and makes significant improvements on prediction performances

Instrumental Variable Estimation for Causal Inference in Longitudinal Data with Time-Dependent Latent Confounders

Causal inference from longitudinal observational data is a challenging problem due to the difficulty in correctly identifying the time-dependent confounders, especially in the presence of latent time-dependent confounders. Instrumental variable (IV) is a powerful tool for addressing the latent confounders issue, but the traditional IV technique cannot deal with latent time-dependent confounders in longitudinal studies. In this work, we propose a novel Time-dependent Instrumental Factor Model (TIFM) for time-varying causal effect estimation from data with latent time-dependent confounders. At each time-step, the proposed TIFM method employs the Recurrent Neural Network (RNN) architecture to infer latent IV, and then uses the inferred latent IV factor for addressing the confounding bias caused by the latent time-dependent confounders. We provide a theoretical analysis for the proposed TIFM method regarding causal effect estimation in longitudinal data. Extensive evaluation with synthetic datasets demonstrates the effectiveness of TIFM in addressing causal effect estimation over time. We further apply TIFM to a climate dataset to showcase the potential of the proposed method in tackling real-world problems.

Disentangled Latent Representation Learning for Tackling the Confounding M-Bias Problem in Causal Inference

In causal inference, it is a fundamental task to estimate the causal effect from observational data. However, latent confounders pose major challenges in causal inference in observational data, for example, confounding bias and M-bias. Recent data-driven causal effect estimators tackle the confounding bias problem via balanced representation learning, but assume no M-bias in the system, thus they fail to handle the M-bias. In this paper, we identify a challenging and unsolved problem caused by a variable that leads to confounding bias and M-bias simultaneously. To address this problem with co-occurring M-bias and confounding bias, we propose a novel Disentangled Latent Representation learning framework for learning latent representations from proxy variables for unbiased Causal effect Estimation (DLRCE) from observational data. Specifically, DLRCE learns three sets of latent representations from the measured proxy variables to adjust for the confounding bias and M-bias. Extensive experiments on both synthetic and three real-world datasets demonstrate that DLRCE significantly outperforms the state-of-the-art estimators in the case of the presence of both confounding bias and M-bias.

Conditional Instrumental Variable Regression with Representation Learning for Causal Inference

This paper studies the challenging problem of estimating causal effects from observational data, in the presence of unobserved confounders. The two-stage least square (TSLS) method and its variants with a standard instrumental variable (IV) are commonly used to eliminate confounding bias, including the bias caused by unobserved confounders, but they rely on the linearity assumption. Besides, the strict condition of unconfounded instruments posed on a standard IV is too strong to be practical. To address these challenging and practical problems of the standard IV method (linearity assumption and the strict condition), in this paper, we use a conditional IV (CIV) to relax the unconfounded instrument condition of standard IV and propose a non-linear CIV regression with Confounding Balancing Representation Learning, CBRL.CIV, for jointly eliminating the confounding bias from unobserved confounders and balancing the observed confounders, without the linearity assumption. We theoretically demonstrate the soundness of CBRL.CIV. Extensive experiments on synthetic and two real-world datasets show the competitive performance of CBRL.CIV against state-of-the-art IV-based estimators and superiority in dealing with the non-linear situation.

Causal Inference with Conditional Front-Door Adjustment and Identifiable Variational Autoencoder

An essential and challenging problem in causal inference is causal effect estimation from observational data. The problem becomes more difficult with the presence of unobserved confounding variables. The front-door adjustment is a practical approach for dealing with unobserved confounding variables. However, the restriction for the standard front-door adjustment is difficult to satisfy in practice. In this paper, we relax some of the restrictions by proposing the concept of conditional front-door (CFD) adjustment and develop the theorem that guarantees the causal effect identifiability of CFD adjustment. Furthermore, as it is often impossible for a CFD variable to be given in practice, it is desirable to learn it from data. By leveraging the ability of deep generative models, we propose CFDiVAE to learn the representation of the CFD adjustment variable directly from data with the identifiable Variational AutoEncoder and formally prove the model identifiability. Extensive experiments on synthetic datasets validate the effectiveness of CFDiVAE and its superiority over existing methods. The experiments also show that the performance of CFDiVAE is less sensitive to the causal strength of unobserved confounding variables. We further apply CFDiVAE to a real-world dataset to demonstrate its potential application.

Learning Conditional Instrumental Variable Representation for Causal Effect Estimation

One of the fundamental challenges in causal inference is to estimate the causal effect of a treatment on its outcome of interest from observational data. However, causal effect estimation often suffers from the impacts of confounding bias caused by unmeasured confounders that affect both the treatment and the outcome. The instrumental variable (IV) approach is a powerful way to eliminate the confounding bias from latent confounders. However, the existing IV-based estimators require a nominated IV, and for a conditional IV (CIV) the corresponding conditioning set too, for causal effect estimation. This limits the application of IV-based estimators. In this paper, by leveraging the advantage of disentangled representation learning, we propose a novel method, named DVAE.CIV, for learning and disentangling the representations of CIV and the representations of its conditioning set for causal effect estimations from data with latent confounders. Extensive experimental results on both synthetic and real-world datasets demonstrate the superiority of the proposed DVAE.CIV method against the existing causal effect estimators.

Causal Effect Estimation with Variational AutoEncoder and the Front Door Criterion

An essential problem in causal inference is estimating causal effects from observational data. The problem becomes more challenging with the presence of unobserved confounders. When there are unobserved confounders, the commonly used back-door adjustment is not applicable. Although the instrumental variable (IV) methods can deal with unobserved confounders, they all assume that the treatment directly affects the outcome, and there is no mediator between the treatment and the outcome. This paper aims to use the front-door criterion to address the challenging problem with the presence of unobserved confounders and mediators. In practice, it is often difficult to identify the set of variables used for front-door adjustment from data. By leveraging the ability of deep generative models in representation learning, we propose FDVAE to learn the representation of a Front-Door adjustment set with a Variational AutoEncoder, instead of trying to search for a set of variables for front-door adjustment. Extensive experiments on synthetic datasets validate the effectiveness of FDVAE and its superiority over existing methods. The experiments also show that the performance of FDVAE is not sensitive to the causal strength of unobserved confounders and is feasible in the case of dimensionality mismatch between learned representations and the ground truth. We further apply the method to three real-world datasets to demonstrate its potential applications.