Partial Transportability for Domain Generalization

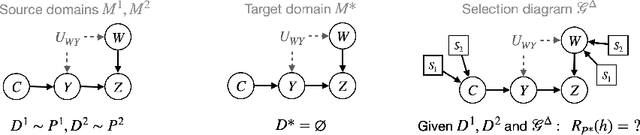
A fundamental task in AI is providing performance guarantees for predictions made in unseen domains. In practice, there can be substantial uncertainty about the distribution of new data, and corresponding variability in the performance of existing predictors. Building on the theory of partial identification and transportability, this paper introduces new results for bounding the value of a functional of the target distribution, such as the generalization error of a classifier, given data from source domains and assumptions about the data generating mechanisms, encoded in causal diagrams. Our contribution is to provide the first general estimation technique for transportability problems, adapting existing parameterization schemes such Neural Causal Models to encode the structural constraints necessary for cross-population inference. We demonstrate the expressiveness and consistency of this procedure and further propose a gradient-based optimization scheme for making scalable inferences in practice. Our results are corroborated with experiments.

Causally Aligned Curriculum Learning

A pervasive challenge in Reinforcement Learning (RL) is the "curse of dimensionality" which is the exponential growth in the state-action space when optimizing a high-dimensional target task. The framework of curriculum learning trains the agent in a curriculum composed of a sequence of related and more manageable source tasks. The expectation is that when some optimal decision rules are shared across source tasks and the target task, the agent could more quickly pick up the necessary skills to behave optimally in the environment, thus accelerating the learning process. However, this critical assumption of invariant optimal decision rules does not necessarily hold in many practical applications, specifically when the underlying environment contains unobserved confounders. This paper studies the problem of curriculum RL through causal lenses. We derive a sufficient graphical condition characterizing causally aligned source tasks, i.e., the invariance of optimal decision rules holds. We further develop an efficient algorithm to generate a causally aligned curriculum, provided with qualitative causal knowledge of the target task. Finally, we validate our proposed methodology through experiments in discrete and continuous confounded tasks with pixel observations.

Counterfactual Realizability

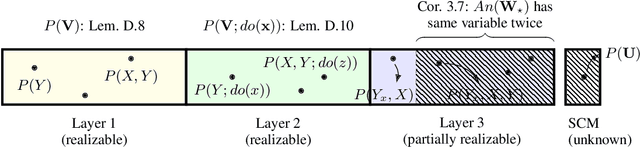
It is commonly believed that, in a real-world environment, samples can only be drawn from observational and interventional distributions, corresponding to Layers 1 and 2 of the Pearl Causal Hierarchy. Layer 3, representing counterfactual distributions, is believed to be inaccessible by definition. However, Bareinboim, Forney, and Pearl (2015) introduced a procedure that allows an agent to sample directly from a counterfactual distribution, leaving open the question of what other counterfactual quantities can be estimated directly via physical experimentation. We resolve this by introducing a formal definition of realizability, the ability to draw samples from a distribution, and then developing a complete algorithm to determine whether an arbitrary counterfactual distribution is realizable given fundamental physical constraints, such as the inability to go back in time and subject the same unit to a different experimental condition. We illustrate the implications of this new framework for counterfactual data collection using motivating examples from causal fairness and causal reinforcement learning. While the baseline approach in these motivating settings typically follows an interventional or observational strategy, we show that a counterfactual strategy provably dominates both.

An Algorithmic Approach for Causal Health Equity: A Look at Race Differentials in Intensive Care Unit (ICU) Outcomes

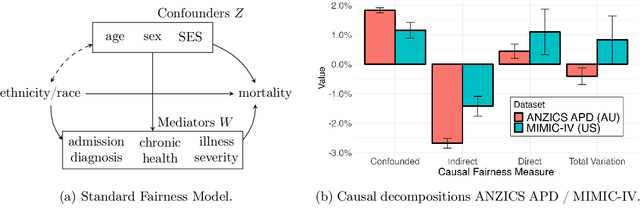
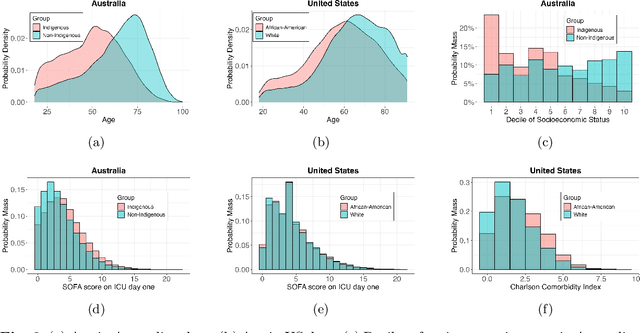
The new era of large-scale data collection and analysis presents an opportunity for diagnosing and understanding the causes of health inequities. In this study, we describe a framework for systematically analyzing health disparities using causal inference. The framework is illustrated by investigating racial and ethnic disparities in intensive care unit (ICU) outcome between majority and minority groups in Australia (Indigenous vs. Non-Indigenous) and the United States (African-American vs. White). We demonstrate that commonly used statistical measures for quantifying inequity are insufficient, and focus on attributing the observed disparity to the causal mechanisms that generate it. We find that minority patients are younger at admission, have worse chronic health, are more likely to be admitted for urgent and non-elective reasons, and have higher illness severity. At the same time, however, we find a protective direct effect of belonging to a minority group, with minority patients showing improved survival compared to their majority counterparts, with all other variables kept equal. We demonstrate that this protective effect is related to the increased probability of being admitted to ICU, with minority patients having an increased risk of ICU admission. We also find that minority patients, while showing improved survival, are more likely to be readmitted to ICU. Thus, due to worse access to primary health care, minority patients are more likely to end up in ICU for preventable conditions, causing a reduction in the mortality rates and creating an effect that appears to be protective. Since the baseline risk of ICU admission may serve as proxy for lack of access to primary care, we developed the Indigenous Intensive Care Equity (IICE) Radar, a monitoring system for tracking the over-utilization of ICU resources by the Indigenous population of Australia across geographical areas.

Testing Causal Models with Hidden Variables in Polynomial Delay via Conditional Independencies

Testing a hypothesized causal model against observational data is a key prerequisite for many causal inference tasks. A natural approach is to test whether the conditional independence relations (CIs) assumed in the model hold in the data. While a model can assume exponentially many CIs (with respect to the number of variables), testing all of them is both impractical and unnecessary. Causal graphs, which encode these CIs in polynomial space, give rise to local Markov properties that enable model testing with a significantly smaller subset of CIs. Model testing based on local properties requires an algorithm to list the relevant CIs. However, existing algorithms for realistic settings with hidden variables and non-parametric distributions can take exponential time to produce even a single CI constraint. In this paper, we introduce the c-component local Markov property (C-LMP) for causal graphs with hidden variables. Since C-LMP can still invoke an exponential number of CIs, we develop a polynomial delay algorithm to list these CIs in poly-time intervals. To our knowledge, this is the first algorithm that enables poly-delay testing of CIs in causal graphs with hidden variables against arbitrary data distributions. Experiments on real-world and synthetic data demonstrate the practicality of our algorithm.

Fairness-Accuracy Trade-Offs: A Causal Perspective

Systems based on machine learning may exhibit discriminatory behavior based on sensitive characteristics such as gender, sex, religion, or race. In light of this, various notions of fairness and methods to quantify discrimination were proposed, leading to the development of numerous approaches for constructing fair predictors. At the same time, imposing fairness constraints may decrease the utility of the decision-maker, highlighting a tension between fairness and utility. This tension is also recognized in legal frameworks, for instance in the disparate impact doctrine of Title VII of the Civil Rights Act of 1964 -- in which specific attention is given to considerations of business necessity -- possibly allowing the usage of proxy variables associated with the sensitive attribute in case a high-enough utility cannot be achieved without them. In this work, we analyze the tension between fairness and accuracy from a causal lens for the first time. We introduce the notion of a path-specific excess loss (PSEL) that captures how much the predictor's loss increases when a causal fairness constraint is enforced. We then show that the total excess loss (TEL), defined as the difference between the loss of predictor fair along all causal pathways vs. an unconstrained predictor, can be decomposed into a sum of more local PSELs. At the same time, enforcing a causal constraint often reduces the disparity between demographic groups. Thus, we introduce a quantity that summarizes the fairness-utility trade-off, called the causal fairness/utility ratio, defined as the ratio of the reduction in discrimination vs. the excess loss from constraining a causal pathway. This quantity is suitable for comparing the fairness-utility trade-off across causal pathways. Finally, as our approach requires causally-constrained fair predictors, we introduce a new neural approach for causally-constrained fair learning.

Mind the Gap: A Causal Perspective on Bias Amplification in Prediction & Decision-Making

Investigating fairness and equity of automated systems has become a critical field of inquiry. Most of the literature in fair machine learning focuses on defining and achieving fairness criteria in the context of prediction, while not explicitly focusing on how these predictions may be used later on in the pipeline. For instance, if commonly used criteria, such as independence or sufficiency, are satisfied for a prediction score $S$ used for binary classification, they need not be satisfied after an application of a simple thresholding operation on $S$ (as commonly used in practice). In this paper, we take an important step to address this issue in numerous statistical and causal notions of fairness. We introduce the notion of a margin complement, which measures how much a prediction score $S$ changes due to a thresholding operation. We then demonstrate that the marginal difference in the optimal 0/1 predictor $\widehat Y$ between groups, written $P(\hat y \mid x_1) - P(\hat y \mid x_0)$, can be causally decomposed into the influences of $X$ on the $L_2$-optimal prediction score $S$ and the influences of $X$ on the margin complement $M$, along different causal pathways (direct, indirect, spurious). We then show that under suitable causal assumptions, the influences of $X$ on the prediction score $S$ are equal to the influences of $X$ on the true outcome $Y$. This yields a new decomposition of the disparity in the predictor $\widehat Y$ that allows us to disentangle causal differences inherited from the true outcome $Y$ that exists in the real world vs. those coming from the optimization procedure itself. This observation highlights the need for more regulatory oversight due to the potential for bias amplification, and to address this issue we introduce new notions of weak and strong business necessity, together with an algorithm for assessing whether these notions are satisfied.

Neural Causal Abstractions

The abilities of humans to understand the world in terms of cause and effect relationships, as well as to compress information into abstract concepts, are two hallmark features of human intelligence. These two topics have been studied in tandem in the literature under the rubric of causal abstractions theory. In practice, it remains an open problem how to best leverage abstraction theory in real-world causal inference tasks, where the true mechanisms are unknown and only limited data is available. In this paper, we develop a new family of causal abstractions by clustering variables and their domains. This approach refines and generalizes previous notions of abstractions to better accommodate individual causal distributions that are spawned by Pearl's causal hierarchy. We show that such abstractions are learnable in practical settings through Neural Causal Models (Xia et al., 2021), enabling the use of the deep learning toolkit to solve various challenging causal inference tasks -- identification, estimation, sampling -- at different levels of granularity. Finally, we integrate these results with representation learning to create more flexible abstractions, moving these results closer to practical applications. Our experiments support the theory and illustrate how to scale causal inferences to high-dimensional settings involving image data.

A Causal Framework for Decomposing Spurious Variations

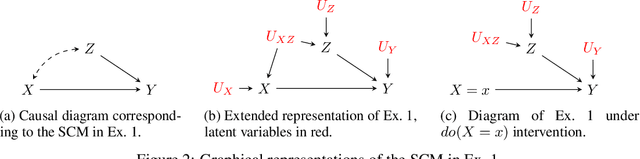
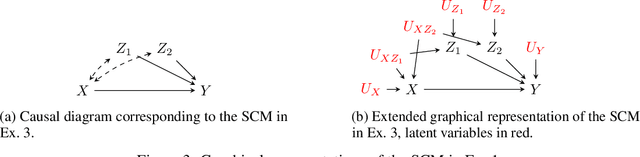
One of the fundamental challenges found throughout the data sciences is to explain why things happen in specific ways, or through which mechanisms a certain variable $X$ exerts influences over another variable $Y$. In statistics and machine learning, significant efforts have been put into developing machinery to estimate correlations across variables efficiently. In causal inference, a large body of literature is concerned with the decomposition of causal effects under the rubric of mediation analysis. However, many variations are spurious in nature, including different phenomena throughout the applied sciences. Despite the statistical power to estimate correlations and the identification power to decompose causal effects, there is still little understanding of the properties of spurious associations and how they can be decomposed in terms of the underlying causal mechanisms. In this manuscript, we develop formal tools for decomposing spurious variations in both Markovian and Semi-Markovian models. We prove the first results that allow a non-parametric decomposition of spurious effects and provide sufficient conditions for the identification of such decompositions. The described approach has several applications, ranging from explainable and fair AI to questions in epidemiology and medicine, and we empirically demonstrate its use on a real-world dataset.

Causal Fairness for Outcome Control

As society transitions towards an AI-based decision-making infrastructure, an ever-increasing number of decisions once under control of humans are now delegated to automated systems. Even though such developments make various parts of society more efficient, a large body of evidence suggests that a great deal of care needs to be taken to make such automated decision-making systems fair and equitable, namely, taking into account sensitive attributes such as gender, race, and religion. In this paper, we study a specific decision-making task called outcome control in which an automated system aims to optimize an outcome variable $Y$ while being fair and equitable. The interest in such a setting ranges from interventions related to criminal justice and welfare, all the way to clinical decision-making and public health. In this paper, we first analyze through causal lenses the notion of benefit, which captures how much a specific individual would benefit from a positive decision, counterfactually speaking, when contrasted with an alternative, negative one. We introduce the notion of benefit fairness, which can be seen as the minimal fairness requirement in decision-making, and develop an algorithm for satisfying it. We then note that the benefit itself may be influenced by the protected attribute, and propose causal tools which can be used to analyze this. Finally, if some of the variations of the protected attribute in the benefit are considered as discriminatory, the notion of benefit fairness may need to be strengthened, which leads us to articulating a notion of causal benefit fairness. Using this notion, we develop a new optimization procedure capable of maximizing $Y$ while ascertaining causal fairness in the decision process.