Evaluating the Goal-Directedness of Large Language Models

To what extent do LLMs use their capabilities towards their given goal? We take this as a measure of their goal-directedness. We evaluate goal-directedness on tasks that require information gathering, cognitive effort, and plan execution, where we use subtasks to infer each model's relevant capabilities. Our evaluations of LLMs from Google DeepMind, OpenAI, and Anthropic show that goal-directedness is relatively consistent across tasks, differs from task performance, and is only moderately sensitive to motivational prompts. Notably, most models are not fully goal-directed. We hope our goal-directedness evaluations will enable better monitoring of LLM progress, and enable more deliberate design choices of agentic properties in LLMs.

Partial Transportability for Domain Generalization

A fundamental task in AI is providing performance guarantees for predictions made in unseen domains. In practice, there can be substantial uncertainty about the distribution of new data, and corresponding variability in the performance of existing predictors. Building on the theory of partial identification and transportability, this paper introduces new results for bounding the value of a functional of the target distribution, such as the generalization error of a classifier, given data from source domains and assumptions about the data generating mechanisms, encoded in causal diagrams. Our contribution is to provide the first general estimation technique for transportability problems, adapting existing parameterization schemes such Neural Causal Models to encode the structural constraints necessary for cross-population inference. We demonstrate the expressiveness and consistency of this procedure and further propose a gradient-based optimization scheme for making scalable inferences in practice. Our results are corroborated with experiments.

Mind the Graph When Balancing Data for Fairness or Robustness

Failures of fairness or robustness in machine learning predictive settings can be due to undesired dependencies between covariates, outcomes and auxiliary factors of variation. A common strategy to mitigate these failures is data balancing, which attempts to remove those undesired dependencies. In this work, we define conditions on the training distribution for data balancing to lead to fair or robust models. Our results display that, in many cases, the balanced distribution does not correspond to selectively removing the undesired dependencies in a causal graph of the task, leading to multiple failure modes and even interference with other mitigation techniques such as regularization. Overall, our results highlight the importance of taking the causal graph into account before performing data balancing.

FunBO: Discovering Acquisition Functions for Bayesian Optimization with FunSearch

The sample efficiency of Bayesian optimization algorithms depends on carefully crafted acquisition functions (AFs) guiding the sequential collection of function evaluations. The best-performing AF can vary significantly across optimization problems, often requiring ad-hoc and problem-specific choices. This work tackles the challenge of designing novel AFs that perform well across a variety of experimental settings. Based on FunSearch, a recent work using Large Language Models (LLMs) for discovery in mathematical sciences, we propose FunBO, an LLM-based method that can be used to learn new AFs written in computer code by leveraging access to a limited number of evaluations for a set of objective functions. We provide the analytic expression of all discovered AFs and evaluate them on various global optimization benchmarks and hyperparameter optimization tasks. We show how FunBO identifies AFs that generalize well in and out of the training distribution of functions, thus outperforming established general-purpose AFs and achieving competitive performance against AFs that are customized to specific function types and are learned via transfer-learning algorithms.

Towards Bounding Causal Effects under Markov Equivalence

Predicting the effect of unseen interventions is a fundamental research question across the data sciences. It is well established that, in general, such questions cannot be answered definitively from observational data, e.g., as a consequence of unobserved confounding. A generalization of this task is to determine non-trivial bounds on causal effects induced by the data, also known as the task of partial causal identification. In the literature, several algorithms have been developed for solving this problem. Most, however, require a known parametric form or a fully specified causal diagram as input, which is usually not available in practical applications. In this paper, we assume as input a less informative structure known as a Partial Ancestral Graph, which represents a Markov equivalence class of causal diagrams and is learnable from observational data. In this more "data-driven" setting, we provide a systematic algorithm to derive bounds on causal effects that can be computed analytically.

Functional Causal Bayesian Optimization

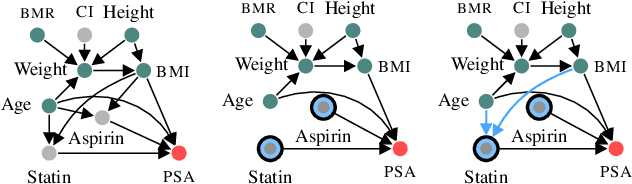
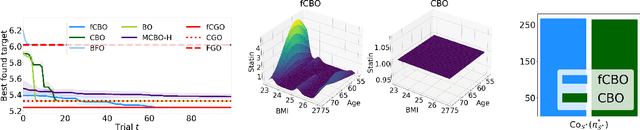
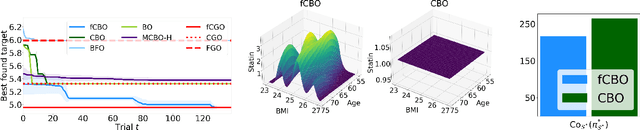
We propose functional causal Bayesian optimization (fCBO), a method for finding interventions that optimize a target variable in a known causal graph. fCBO extends the CBO family of methods to enable functional interventions, which set a variable to be a deterministic function of other variables in the graph. fCBO models the unknown objectives with Gaussian processes whose inputs are defined in a reproducing kernel Hilbert space, thus allowing to compute distances among vector-valued functions. In turn, this enables to sequentially select functions to explore by maximizing an expected improvement acquisition functional while keeping the typical computational tractability of standard BO settings. We introduce graphical criteria that establish when considering functional interventions allows attaining better target effects, and conditions under which selected interventions are also optimal for conditional target effects. We demonstrate the benefits of the method in a synthetic and in a real-world causal graph.

Continuous-Time Modeling of Counterfactual Outcomes Using Neural Controlled Differential Equations

Estimating counterfactual outcomes over time has the potential to unlock personalized healthcare by assisting decision-makers to answer ''what-iF'' questions. Existing causal inference approaches typically consider regular, discrete-time intervals between observations and treatment decisions and hence are unable to naturally model irregularly sampled data, which is the common setting in practice. To handle arbitrary observation patterns, we interpret the data as samples from an underlying continuous-time process and propose to model its latent trajectory explicitly using the mathematics of controlled differential equations. This leads to a new approach, the Treatment Effect Neural Controlled Differential Equation (TE-CDE), that allows the potential outcomes to be evaluated at any time point. In addition, adversarial training is used to adjust for time-dependent confounding which is critical in longitudinal settings and is an added challenge not encountered in conventional time-series. To assess solutions to this problem, we propose a controllable simulation environment based on a model of tumor growth for a range of scenarios with irregular sampling reflective of a variety of clinical scenarios. TE-CDE consistently outperforms existing approaches in all simulated scenarios with irregular sampling.

Generalization bounds and algorithms for estimating conditional average treatment effect of dosage

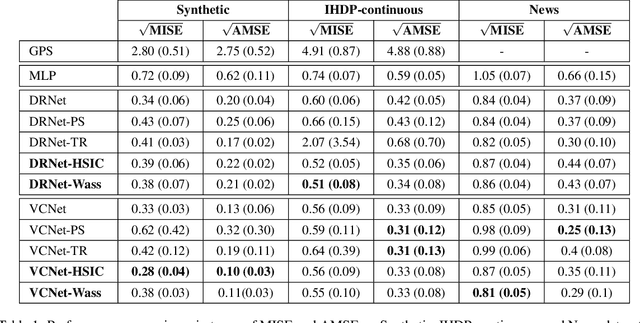
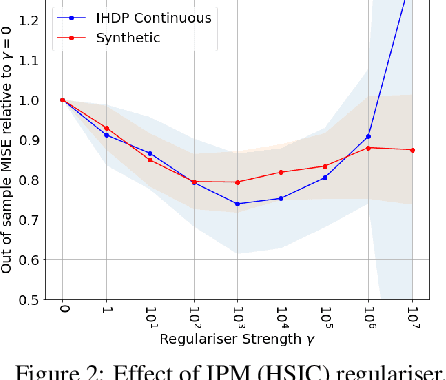
We investigate the task of estimating the conditional average causal effect of treatment-dosage pairs from a combination of observational data and assumptions on the causal relationships in the underlying system. This has been a longstanding challenge for fields of study such as epidemiology or economics that require a treatment-dosage pair to make decisions but may not be able to run randomized trials to precisely quantify their effect and heterogeneity across individuals. In this paper, we extend (Shalit et al, 2017) to give new bounds on the counterfactual generalization error in the context of a continuous dosage parameter which relies on a different approach to defining counterfactuals and assignment bias adjustment. This result then guides the definition of new learning objectives that can be used to train representation learning algorithms for which we show empirically new state-of-the-art performance results across several benchmark datasets for this problem, including in comparison to doubly-robust estimation methods.

MIRACLE: Causally-Aware Imputation via Learning Missing Data Mechanisms

Missing data is an important problem in machine learning practice. Starting from the premise that imputation methods should preserve the causal structure of the data, we develop a regularization scheme that encourages any baseline imputation method to be causally consistent with the underlying data generating mechanism. Our proposal is a causally-aware imputation algorithm (MIRACLE). MIRACLE iteratively refines the imputation of a baseline by simultaneously modeling the missingness generating mechanism, encouraging imputation to be consistent with the causal structure of the data. We conduct extensive experiments on synthetic and a variety of publicly available datasets to show that MIRACLE is able to consistently improve imputation over a variety of benchmark methods across all three missingness scenarios: at random, completely at random, and not at random.

Consistency of mechanistic causal discovery in continuous-time using Neural ODEs

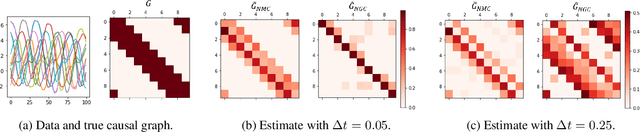
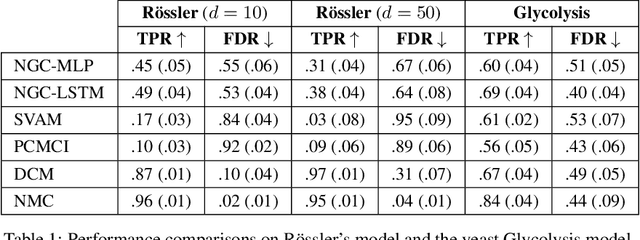
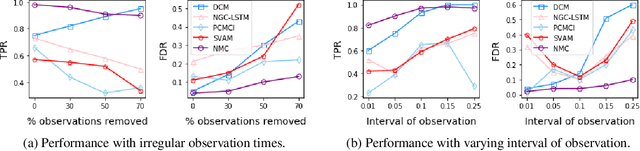
The discovery of causal mechanisms from time series data is a key problem in fields working with complex systems. Most identifiability results and learning algorithms assume the underlying dynamics to be discrete in time. Comparatively few, in contrast, explicitly define causal associations in infinitesimal intervals of time, independently of the scale of observation and of the regularity of sampling. In this paper, we consider causal discovery in continuous-time for the study of dynamical systems. We prove that for vector fields parameterized in a large class of neural networks, adaptive regularization schemes consistently recover causal graphs in systems of ordinary differential equations (ODEs). Using this insight, we propose a causal discovery algorithm based on penalized Neural ODEs that we show to be applicable to the general setting of irregularly-sampled multivariate time series and to strongly outperform the state of the art.