Generalization bounds and algorithms for estimating conditional average treatment effect of dosage

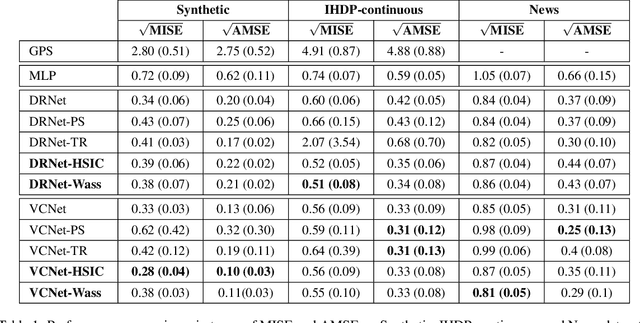
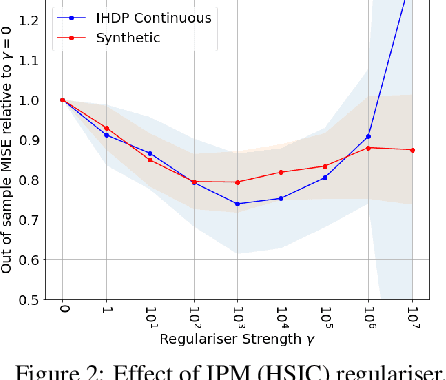
We investigate the task of estimating the conditional average causal effect of treatment-dosage pairs from a combination of observational data and assumptions on the causal relationships in the underlying system. This has been a longstanding challenge for fields of study such as epidemiology or economics that require a treatment-dosage pair to make decisions but may not be able to run randomized trials to precisely quantify their effect and heterogeneity across individuals. In this paper, we extend (Shalit et al, 2017) to give new bounds on the counterfactual generalization error in the context of a continuous dosage parameter which relies on a different approach to defining counterfactuals and assignment bias adjustment. This result then guides the definition of new learning objectives that can be used to train representation learning algorithms for which we show empirically new state-of-the-art performance results across several benchmark datasets for this problem, including in comparison to doubly-robust estimation methods.

Learning medical triage from clinicians using Deep Q-Learning

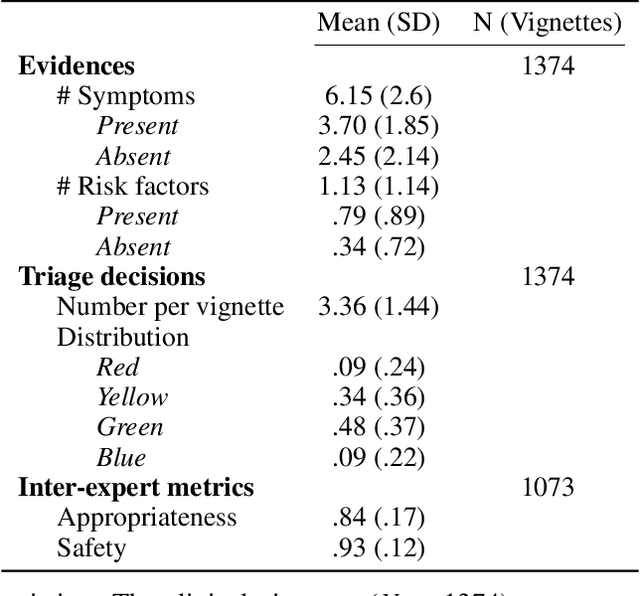
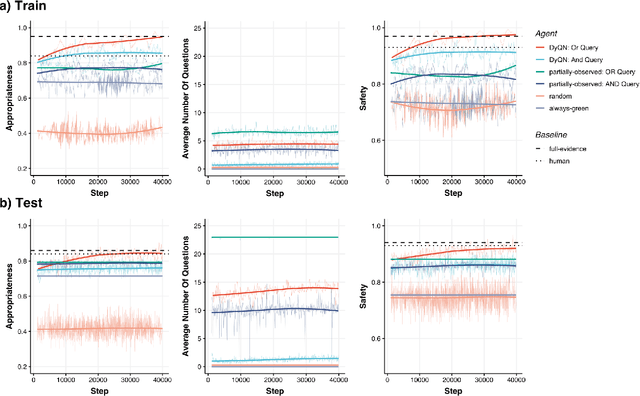
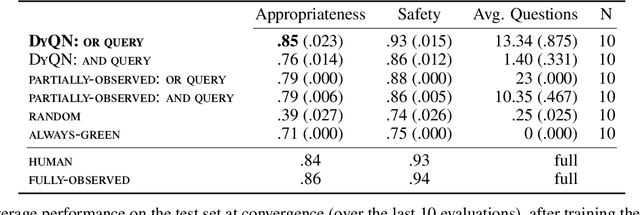
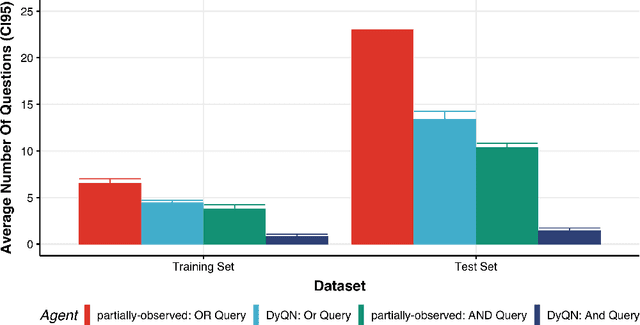
Medical Triage is of paramount importance to healthcare systems, allowing for the correct orientation of patients and allocation of the necessary resources to treat them adequately. While reliable decision-tree methods exist to triage patients based on their presentation, those trees implicitly require human inference and are not immediately applicable in a fully automated setting. On the other hand, learning triage policies directly from experts may correct for some of the limitations of hard-coded decision-trees. In this work, we present a Deep Reinforcement Learning approach (a variant of DeepQ-Learning) to triage patients using curated clinical vignettes. The dataset, consisting of 1374 clinical vignettes, was created by medical doctors to represent real-life cases. Each vignette is associated with an average of 3.8 expert triage decisions given by medical doctors relying solely on medical history. We show that this approach is on a par with human performance, yielding safe triage decisions in 94% of cases, and matching expert decisions in 85% of cases. The trained agent learns when to stop asking questions, acquires optimized decision policies requiring less evidence than supervised approaches, and adapts to the novelty of a situation by asking for more information. Overall, we demonstrate that a Deep Reinforcement Learning approach can learn effective medical triage policies directly from expert decisions, without requiring expert knowledge engineering. This approach is scalable and can be deployed in healthcare settings or geographical regions with distinct triage specifications, or where trained experts are scarce, to improve decision making in the early stage of care.

Maximum Entropy Vector Kernels for MIMO system identification

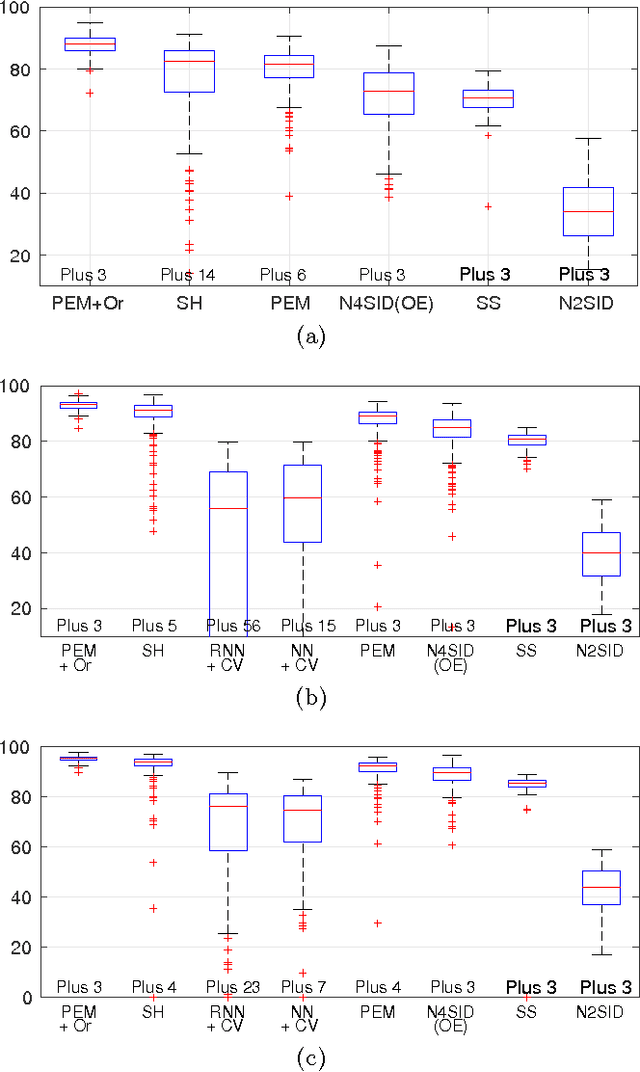
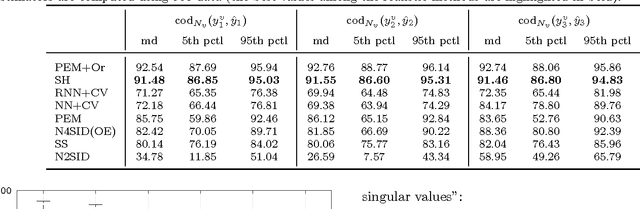
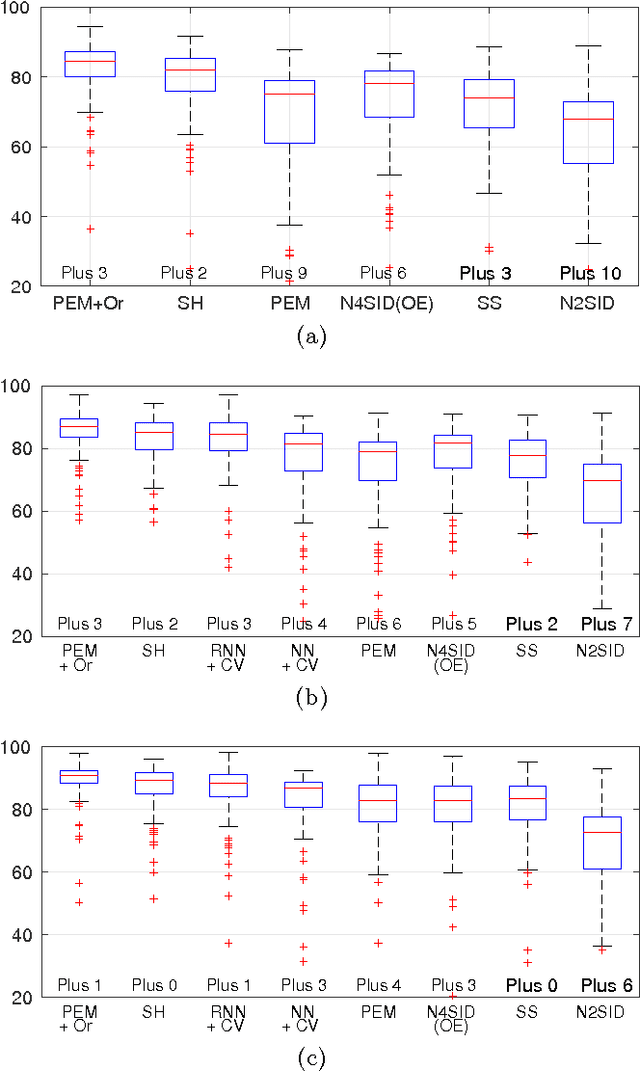
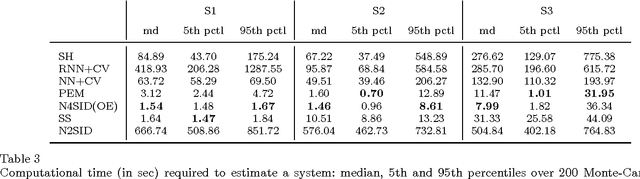
Recent contributions have framed linear system identification as a nonparametric regularized inverse problem. Relying on $\ell_2$-type regularization which accounts for the stability and smoothness of the impulse response to be estimated, these approaches have been shown to be competitive w.r.t classical parametric methods. In this paper, adopting Maximum Entropy arguments, we derive a new $\ell_2$ penalty deriving from a vector-valued kernel; to do so we exploit the structure of the Hankel matrix, thus controlling at the same time complexity, measured by the McMillan degree, stability and smoothness of the identified models. As a special case we recover the nuclear norm penalty on the squared block Hankel matrix. In contrast with previous literature on reweighted nuclear norm penalties, our kernel is described by a small number of hyper-parameters, which are iteratively updated through marginal likelihood maximization; constraining the structure of the kernel acts as a (hyper)regularizer which helps controlling the effective degrees of freedom of our estimator. To optimize the marginal likelihood we adapt a Scaled Gradient Projection (SGP) algorithm which is proved to be significantly computationally cheaper than other first and second order off-the-shelf optimization methods. The paper also contains an extensive comparison with many state-of-the-art methods on several Monte-Carlo studies, which confirms the effectiveness of our procedure.

On-line Bayesian System Identification

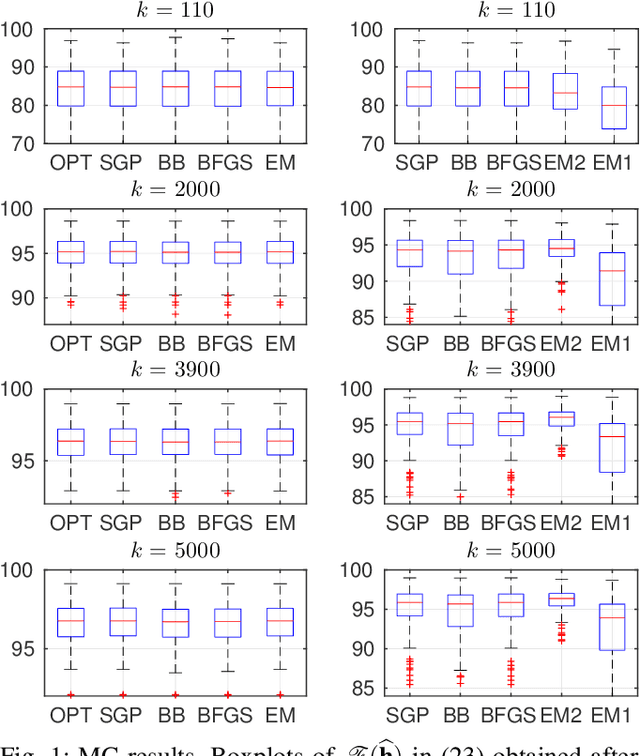
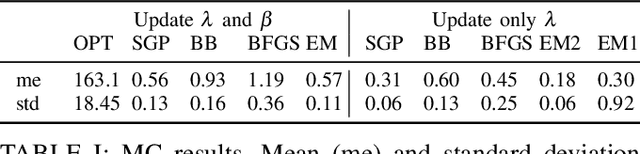
We consider an on-line system identification setting, in which new data become available at given time steps. In order to meet real-time estimation requirements, we propose a tailored Bayesian system identification procedure, in which the hyper-parameters are still updated through Marginal Likelihood maximization, but after only one iteration of a suitable iterative optimization algorithm. Both gradient methods and the EM algorithm are considered for the Marginal Likelihood optimization. We compare this "1-step" procedure with the standard one, in which the optimization method is run until convergence to a local minimum. The experiments we perform confirm the effectiveness of the approach we propose.

Bayesian and regularization approaches to multivariable linear system identification: the role of rank penalties

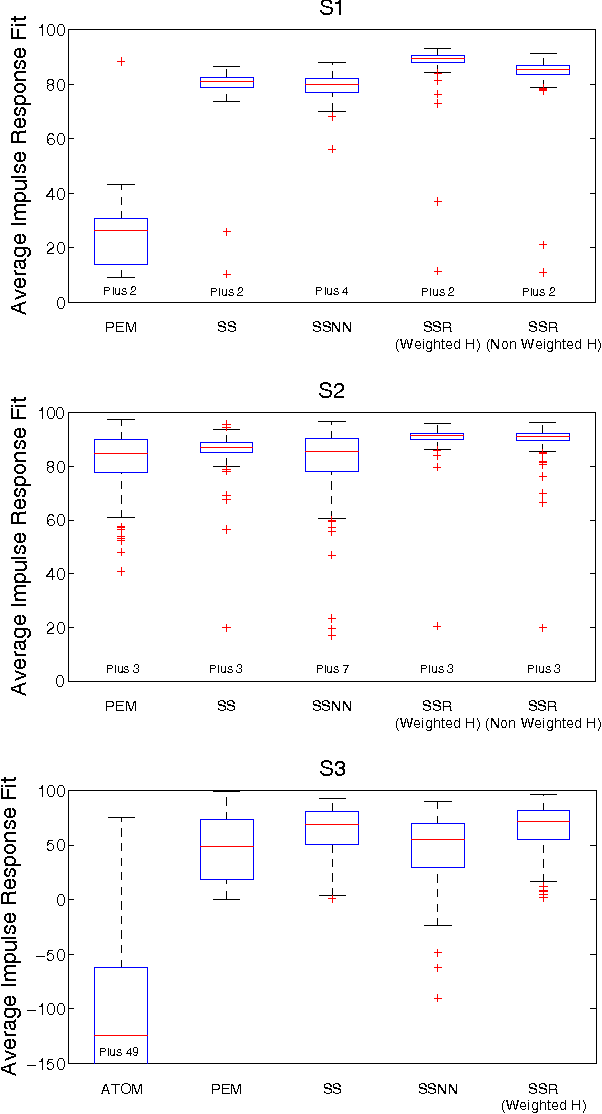
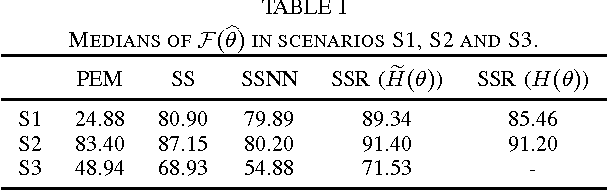
Recent developments in linear system identification have proposed the use of non-parameteric methods, relying on regularization strategies, to handle the so-called bias/variance trade-off. This paper introduces an impulse response estimator which relies on an $\ell_2$-type regularization including a rank-penalty derived using the log-det heuristic as a smooth approximation to the rank function. This allows to account for different properties of the estimated impulse response (e.g. smoothness and stability) while also penalizing high-complexity models. This also allows to account and enforce coupling between different input-output channels in MIMO systems. According to the Bayesian paradigm, the parameters defining the relative weight of the two regularization terms as well as the structure of the rank penalty are estimated optimizing the marginal likelihood. Once these hyperameters have been estimated, the impulse response estimate is available in closed form. Experiments show that the proposed method is superior to the estimator relying on the "classic" $\ell_2$-regularization alone as well as those based in atomic and nuclear norm.