A Meta-Learning Approach to Bayesian Causal Discovery

Discovering a unique causal structure is difficult due to both inherent identifiability issues, and the consequences of finite data. As such, uncertainty over causal structures, such as those obtained from a Bayesian posterior, are often necessary for downstream tasks. Finding an accurate approximation to this posterior is challenging, due to the large number of possible causal graphs, as well as the difficulty in the subproblem of finding posteriors over the functional relationships of the causal edges. Recent works have used meta-learning to view the problem of estimating the maximum a-posteriori causal graph as supervised learning. Yet, these methods are limited when estimating the full posterior as they fail to encode key properties of the posterior, such as correlation between edges and permutation equivariance with respect to nodes. Further, these methods also cannot reliably sample from the posterior over causal structures. To address these limitations, we propose a Bayesian meta learning model that allows for sampling causal structures from the posterior and encodes these key properties. We compare our meta-Bayesian causal discovery against existing Bayesian causal discovery methods, demonstrating the advantages of directly learning a posterior over causal structure.

Continuous Bayesian Model Selection for Multivariate Causal Discovery

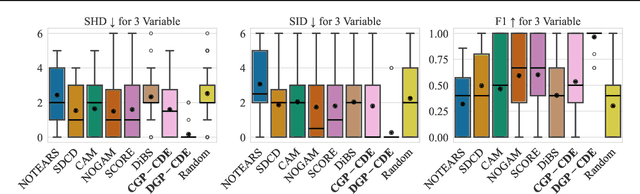
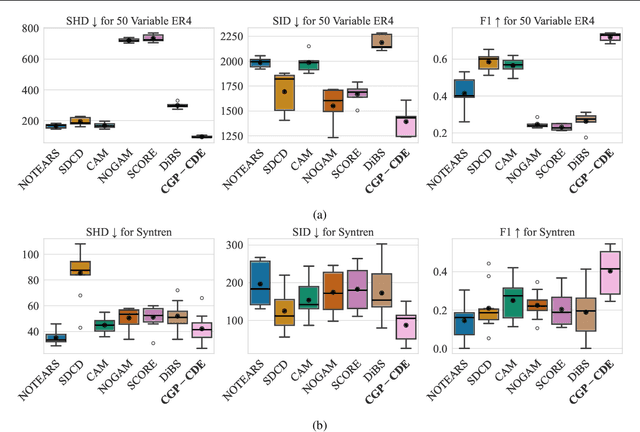
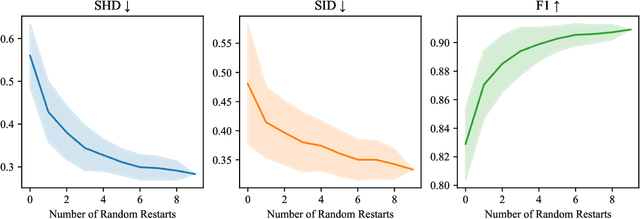
Current causal discovery approaches require restrictive model assumptions or assume access to interventional data to ensure structure identifiability. These assumptions often do not hold in real-world applications leading to a loss of guarantees and poor accuracy in practice. Recent work has shown that, in the bivariate case, Bayesian model selection can greatly improve accuracy by exchanging restrictive modelling for more flexible assumptions, at the cost of a small probability of error. We extend the Bayesian model selection approach to the important multivariate setting by making the large discrete selection problem scalable through a continuous relaxation. We demonstrate how for our choice of Bayesian non-parametric model, the Causal Gaussian Process Conditional Density Estimator (CGP-CDE), an adjacency matrix can be constructed from the model hyperparameters. This adjacency matrix is then optimised using the marginal likelihood and an acyclicity regulariser, outputting the maximum a posteriori causal graph. We demonstrate the competitiveness of our approach on both synthetic and real-world datasets, showing it is possible to perform multivariate causal discovery without infeasible assumptions using Bayesian model selection.

Causal Discovery using Bayesian Model Selection

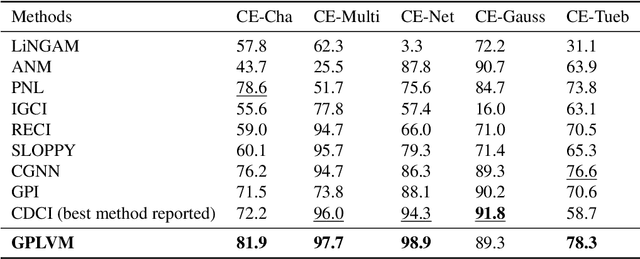
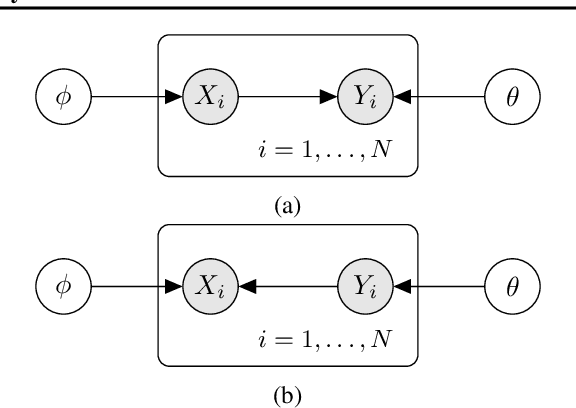
With only observational data on two variables, and without other assumptions, it is not possible to infer which one causes the other. Much of the causal literature has focused on guaranteeing identifiability of causal direction in statistical models for datasets where strong assumptions hold, such as additive noise or restrictions on parameter count. These methods are then subsequently tested on realistic datasets, most of which violate their assumptions. Building on previous attempts, we show how to use causal assumptions within the Bayesian framework. This allows us to specify models with realistic assumptions, while also encoding independent causal mechanisms, leading to an asymmetry between the causal directions. Identifying causal direction then becomes a Bayesian model selection problem. We analyse why Bayesian model selection works for known identifiable cases and flexible model classes, while also providing correctness guarantees about its behaviour. To demonstrate our approach, we construct a Bayesian non-parametric model that can flexibly model the joint. We then outperform previous methods on a wide range of benchmark datasets with varying data generating assumptions showing the usefulness of our method.

Generalization bounds and algorithms for estimating conditional average treatment effect of dosage

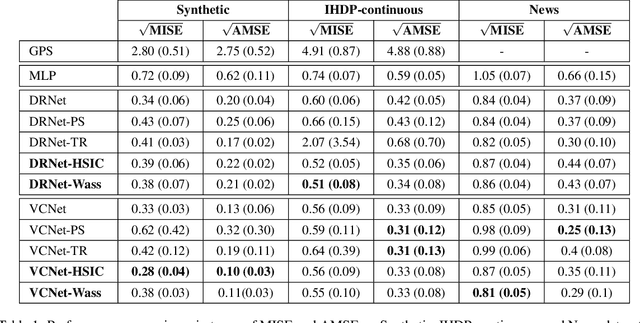
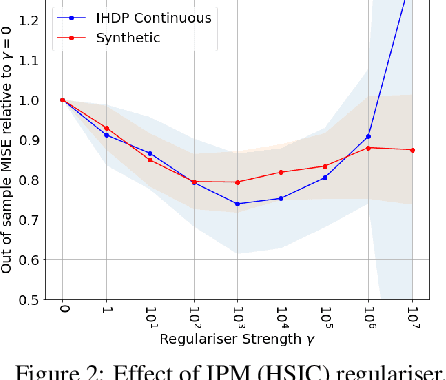
We investigate the task of estimating the conditional average causal effect of treatment-dosage pairs from a combination of observational data and assumptions on the causal relationships in the underlying system. This has been a longstanding challenge for fields of study such as epidemiology or economics that require a treatment-dosage pair to make decisions but may not be able to run randomized trials to precisely quantify their effect and heterogeneity across individuals. In this paper, we extend (Shalit et al, 2017) to give new bounds on the counterfactual generalization error in the context of a continuous dosage parameter which relies on a different approach to defining counterfactuals and assignment bias adjustment. This result then guides the definition of new learning objectives that can be used to train representation learning algorithms for which we show empirically new state-of-the-art performance results across several benchmark datasets for this problem, including in comparison to doubly-robust estimation methods.

Integrating overlapping datasets using bivariate causal discovery

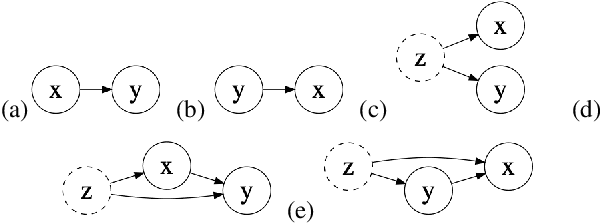
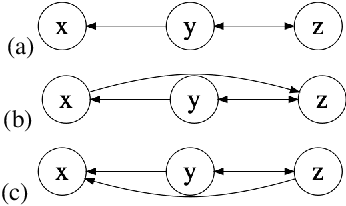
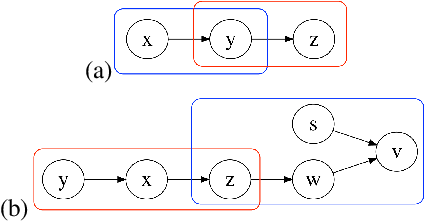
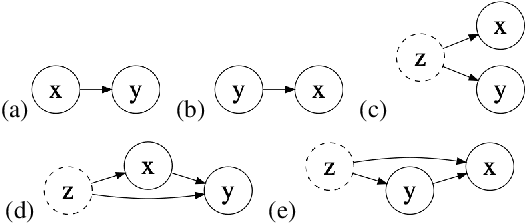
Causal knowledge is vital for effective reasoning in science, as causal relations, unlike correlations, allow one to reason about the outcomes of interventions. Algorithms that can discover causal relations from observational data are based on the assumption that all variables have been jointly measured in a single dataset. In many cases this assumption fails. Previous approaches to overcoming this shortcoming devised algorithms that returned all joint causal structures consistent with the conditional independence information contained in each individual dataset. But, as conditional independence tests only determine causal structure up to Markov equivalence, the number of consistent joint structures returned by these approaches can be quite large. The last decade has seen the development of elegant algorithms for discovering causal relations beyond conditional independence, which can distinguish among Markov equivalent structures. In this work we adapt and extend these so-called bivariate causal discovery algorithms to the problem of learning consistent causal structures from multiple datasets with overlapping variables belonging to the same generating process, providing a sound and complete algorithm that outperforms previous approaches on synthetic and real data.