Alessandro Chiuso
A novel Deep Neural Network architecture for non-linear system identification
Jun 06, 2021
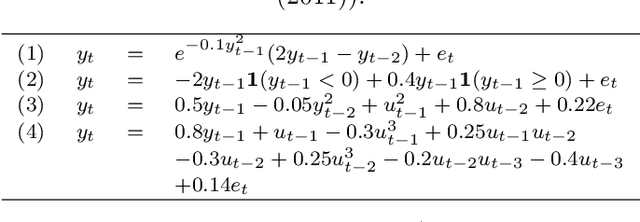
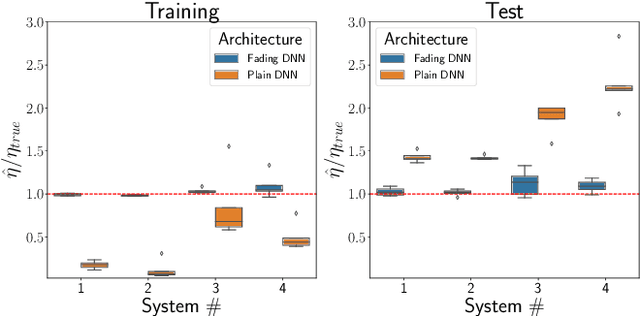
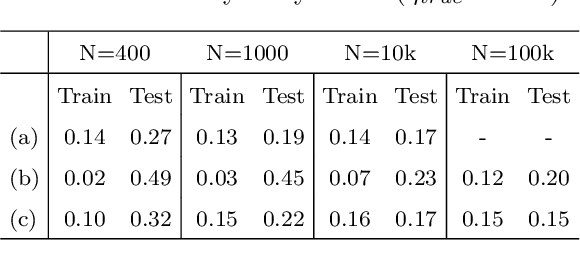
Abstract:We present a novel Deep Neural Network (DNN) architecture for non-linear system identification. We foster generalization by constraining DNN representational power. To do so, inspired by fading memory systems, we introduce inductive bias (on the architecture) and regularization (on the loss function). This architecture allows for automatic complexity selection based solely on available data, in this way the number of hyper-parameters that must be chosen by the user is reduced. Exploiting the highly parallelizable DNN framework (based on Stochastic optimization methods) we successfully apply our method to large scale datasets.
Estimating Koopman operators for nonlinear dynamical systems: a nonparametric approach
Mar 25, 2021

Abstract:The Koopman operator is a mathematical tool that allows for a linear description of non-linear systems, but working in infinite dimensional spaces. Dynamic Mode Decomposition and Extended Dynamic Mode Decomposition are amongst the most popular finite dimensional approximation. In this paper we capture their core essence as a dual version of the same framework, incorporating them into the Kernel framework. To do so, we leverage the RKHS as a suitable space for learning the Koopman dynamics, thanks to its intrinsic finite-dimensional nature, shaped by data. We finally establish a strong link between kernel methods and Koopman operators, leading to the estimation of the latter through Kernel functions. We provide also simulations for comparison with standard procedures.
Derivative-free online learning of inverse dynamics models
Sep 13, 2018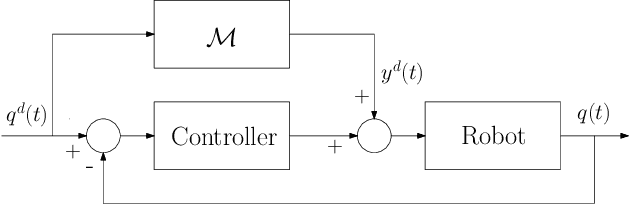
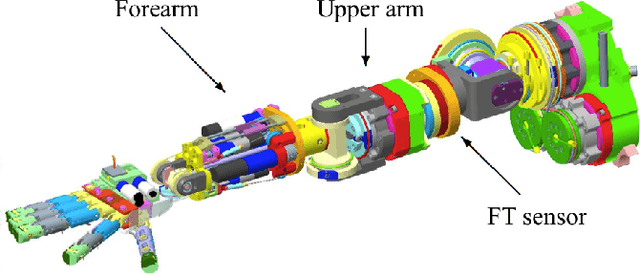
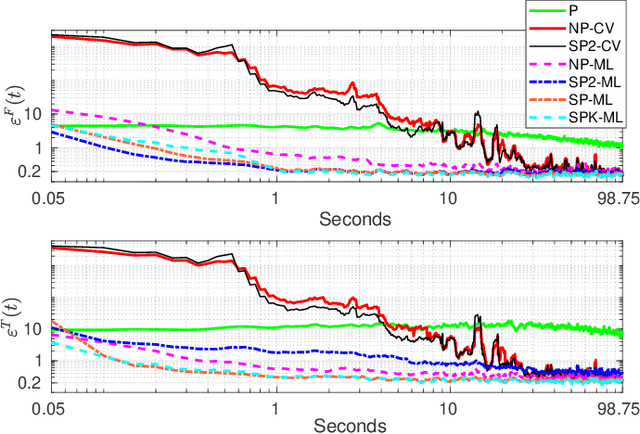
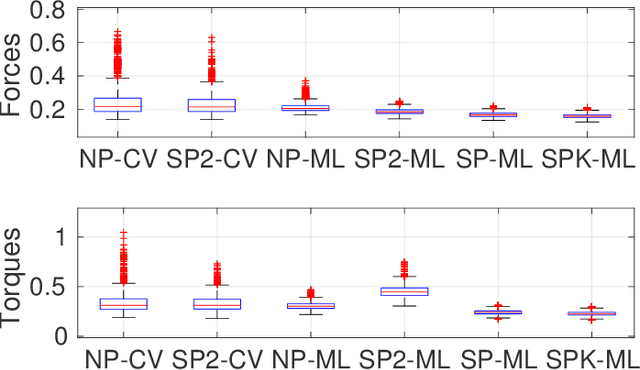
Abstract:This paper discusses online algorithms for inverse dynamics modelling in robotics. Several model classes including rigid body dynamics (RBD) models, data-driven models and semiparametric models (which are a combination of the previous two classes) are placed in a common framework. While model classes used in the literature typically exploit joint velocities and accelerations, which need to be approximated resorting to numerical differentiation schemes, in this paper a new `derivative-free' framework is proposed that does not require this preprocessing step. An extensive experimental study with real data from the right arm of the iCub robot is presented, comparing different model classes and estimation procedures, showing that the proposed `derivative-free' methods outperform existing methodologies.
Online semi-parametric learning for inverse dynamics modeling
Oct 09, 2016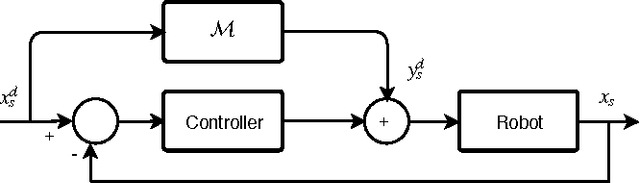



Abstract:This paper presents a semi-parametric algorithm for online learning of a robot inverse dynamics model. It combines the strength of the parametric and non-parametric modeling. The former exploits the rigid body dynamics equa- tion, while the latter exploits a suitable kernel function. We provide an extensive comparison with other methods from the literature using real data from the iCub humanoid robot. In doing so we also compare two different techniques, namely cross validation and marginal likelihood optimization, for estimating the hyperparameters of the kernel function.
Maximum Entropy Vector Kernels for MIMO system identification
Sep 29, 2016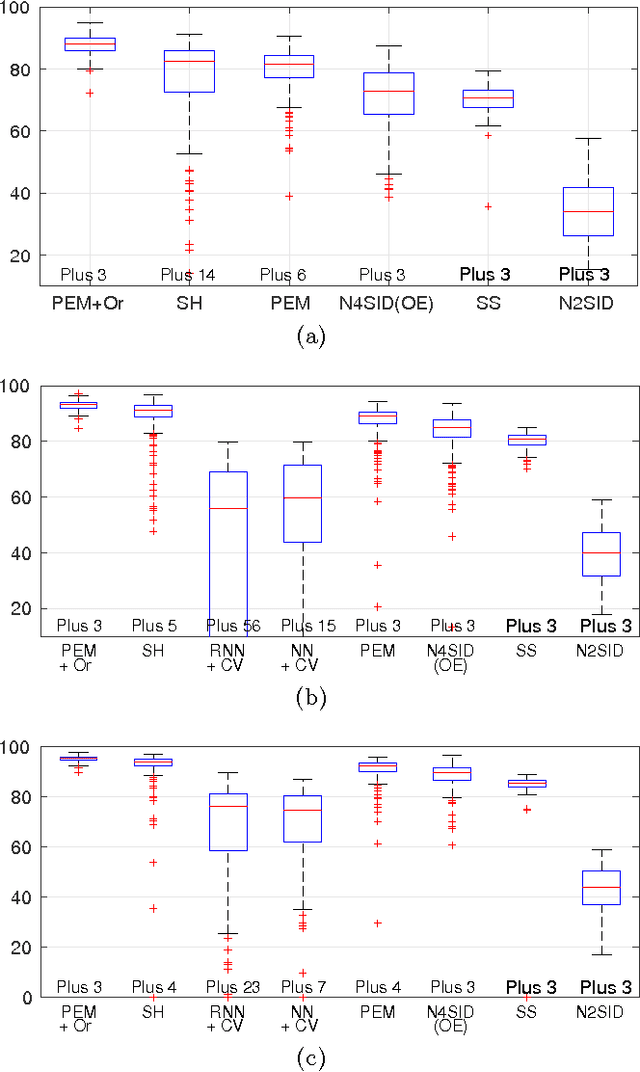
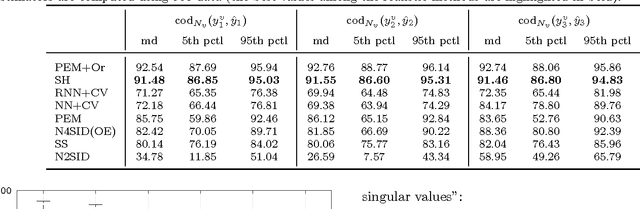
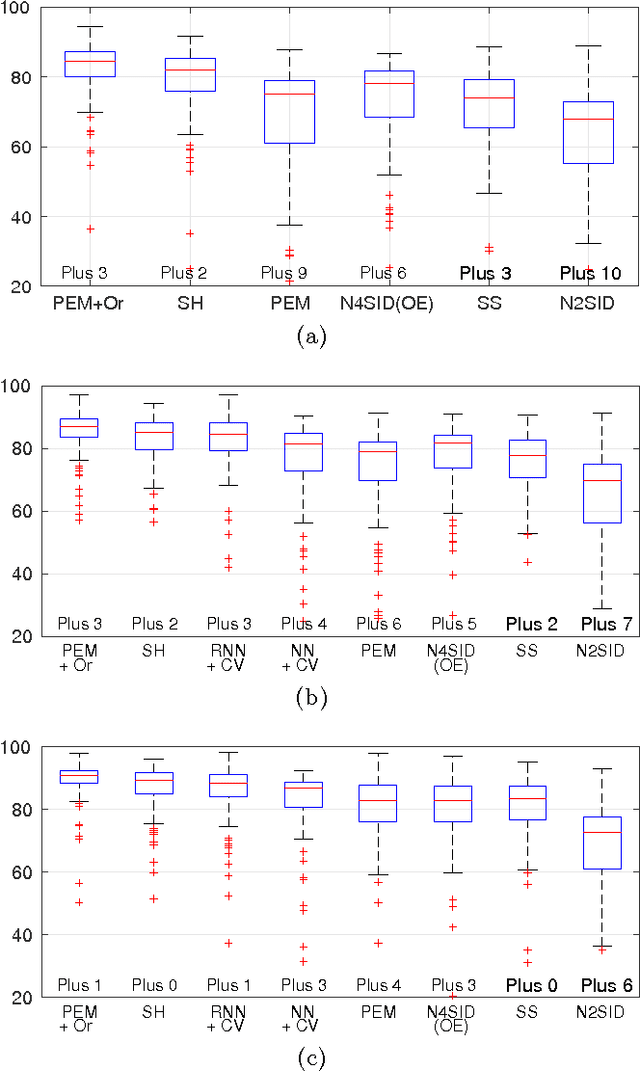
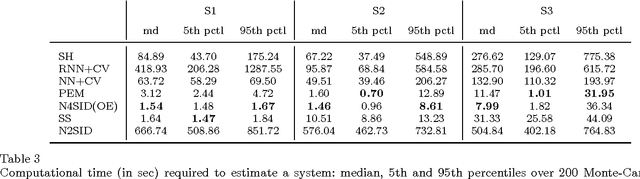
Abstract:Recent contributions have framed linear system identification as a nonparametric regularized inverse problem. Relying on $\ell_2$-type regularization which accounts for the stability and smoothness of the impulse response to be estimated, these approaches have been shown to be competitive w.r.t classical parametric methods. In this paper, adopting Maximum Entropy arguments, we derive a new $\ell_2$ penalty deriving from a vector-valued kernel; to do so we exploit the structure of the Hankel matrix, thus controlling at the same time complexity, measured by the McMillan degree, stability and smoothness of the identified models. As a special case we recover the nuclear norm penalty on the squared block Hankel matrix. In contrast with previous literature on reweighted nuclear norm penalties, our kernel is described by a small number of hyper-parameters, which are iteratively updated through marginal likelihood maximization; constraining the structure of the kernel acts as a (hyper)regularizer which helps controlling the effective degrees of freedom of our estimator. To optimize the marginal likelihood we adapt a Scaled Gradient Projection (SGP) algorithm which is proved to be significantly computationally cheaper than other first and second order off-the-shelf optimization methods. The paper also contains an extensive comparison with many state-of-the-art methods on several Monte-Carlo studies, which confirms the effectiveness of our procedure.
Visual Representations: Defining Properties and Deep Approximations
Feb 29, 2016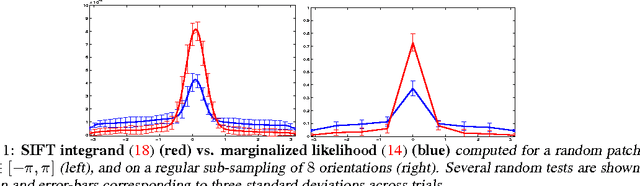

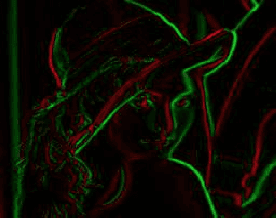

Abstract:Visual representations are defined in terms of minimal sufficient statistics of visual data, for a class of tasks, that are also invariant to nuisance variability. Minimal sufficiency guarantees that we can store a representation in lieu of raw data with smallest complexity and no performance loss on the task at hand. Invariance guarantees that the statistic is constant with respect to uninformative transformations of the data. We derive analytical expressions for such representations and show they are related to feature descriptors commonly used in computer vision, as well as to convolutional neural networks. This link highlights the assumptions and approximations tacitly assumed by these methods and explains empirical practices such as clamping, pooling and joint normalization.
On-line Bayesian System Identification
Jan 17, 2016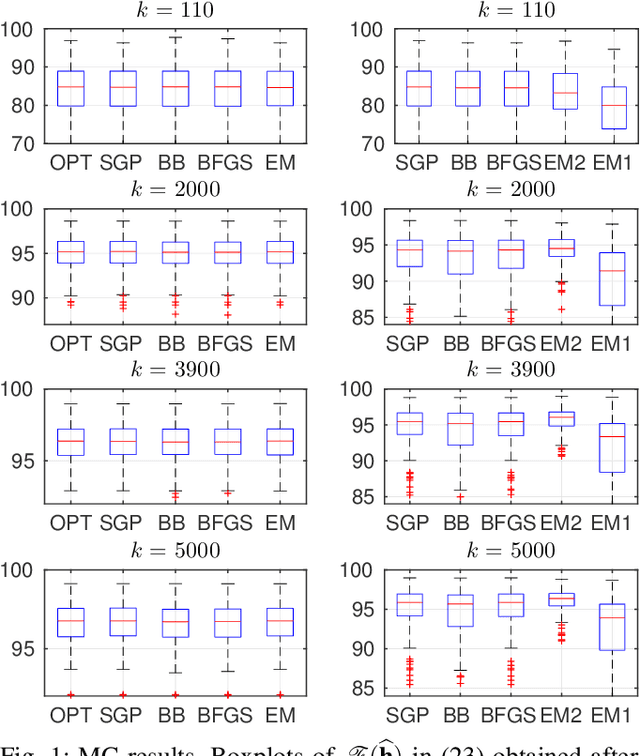
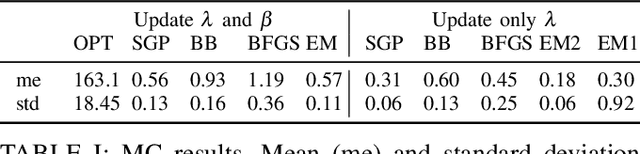
Abstract:We consider an on-line system identification setting, in which new data become available at given time steps. In order to meet real-time estimation requirements, we propose a tailored Bayesian system identification procedure, in which the hyper-parameters are still updated through Marginal Likelihood maximization, but after only one iteration of a suitable iterative optimization algorithm. Both gradient methods and the EM algorithm are considered for the Marginal Likelihood optimization. We compare this "1-step" procedure with the standard one, in which the optimization method is run until convergence to a local minimum. The experiments we perform confirm the effectiveness of the approach we propose.
A Bayesian Approach to Sparse plus Low rank Network Identification
Sep 26, 2015
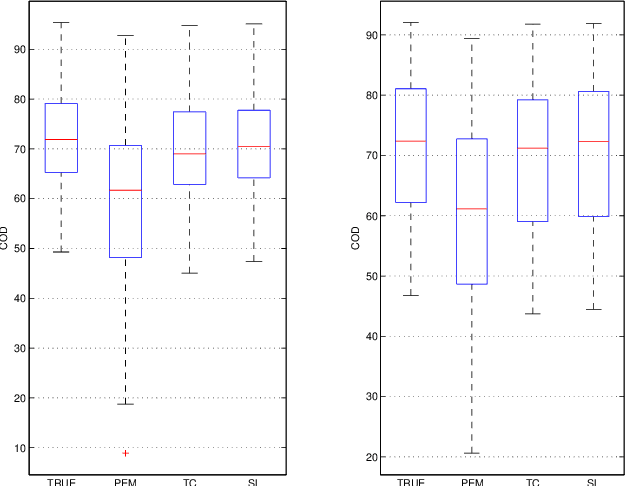


Abstract:We consider the problem of modeling multivariate time series with parsimonious dynamical models which can be represented as sparse dynamic Bayesian networks with few latent nodes. This structure translates into a sparse plus low rank model. In this paper, we propose a Gaussian regression approach to identify such a model.
Regularized linear system identification using atomic, nuclear and kernel-based norms: the role of the stability constraint
Jul 02, 2015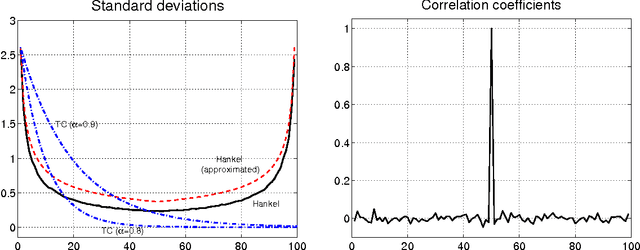
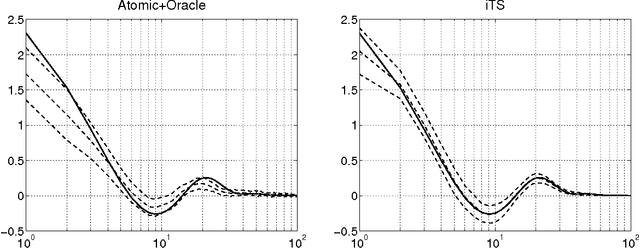


Abstract:Inspired by ideas taken from the machine learning literature, new regularization techniques have been recently introduced in linear system identification. In particular, all the adopted estimators solve a regularized least squares problem, differing in the nature of the penalty term assigned to the impulse response. Popular choices include atomic and nuclear norms (applied to Hankel matrices) as well as norms induced by the so called stable spline kernels. In this paper, a comparative study of estimators based on these different types of regularizers is reported. Our findings reveal that stable spline kernels outperform approaches based on atomic and nuclear norms since they suitably embed information on impulse response stability and smoothness. This point is illustrated using the Bayesian interpretation of regularization. We also design a new class of regularizers defined by "integral" versions of stable spline/TC kernels. Under quite realistic experimental conditions, the new estimators outperform classical prediction error methods also when the latter are equipped with an oracle for model order selection.
Identification of stable models via nonparametric prediction error methods
Jul 02, 2015


Abstract:A new Bayesian approach to linear system identification has been proposed in a series of recent papers. The main idea is to frame linear system identification as predictor estimation in an infinite dimensional space, with the aid of regularization/Bayesian techniques. This approach guarantees the identification of stable predictors based on the prediction error minimization. Unluckily, the stability of the predictors does not guarantee the stability of the impulse response of the system. In this paper we propose and compare various techniques to address this issue. Simulations results comparing these techniques will be provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge