Giuseppe De Nicolao
Regularization methods for the short-term forecasting of the Italian electric load
Dec 08, 2021



Abstract:The problem of forecasting the whole 24 profile of the Italian electric load is addressed as a multitask learning problem, whose complexity is kept under control via alternative regularization methods. In view of the quarter-hourly samplings, 96 predictors are used, each of which linearly depends on 96 regressors. The 96x96 matrix weights form a 96x96 matrix, that can be seen and displayed as a surface sampled on a square domain. Different regularization and sparsity approaches to reduce the degrees of freedom of the surface were explored, comparing the obtained forecasts with those of the Italian Transmission System Operator Terna. Besides outperforming Terna in terms of quarter-hourly mean absolute percentage error and mean absolute error, the prediction residuals turned out to be weakly correlated with Terna, which suggests that further improvement could ensue from forecasts aggregation. In fact, the aggregated forecasts yielded further relevant drops in terms of quarter-hourly and daily mean absolute percentage error, mean absolute error and root mean square error (up to 30%) over the three test years considered.
Identification of AC Networks via Online Learning
Mar 13, 2020



Abstract:The increasing integration of intermittent renewable generation in power networks calls for novel planning and control methodologies, which hinge on detailed knowledge of the grid. However, reliable information concerning the system topology and parameters may be missing or outdated for temporally varying AC networks. This paper proposes an online learning procedure to estimate the admittance matrix of an AC network capturing topological information and line parameters. We start off by providing a recursive identification algorithm that exploits phasor measurements of voltages and currents. With the goal of accelerating convergence, we subsequently complement our base algorithm with a design-of-experiment procedure, which maximizes the information content of data at each step by computing optimal voltage excitations. Our approach improves on existing techniques and its effectiveness is substantiated by numerical studies on a 6-bus AC network.
Short-term forecasting of Italian gas demand
Jan 31, 2019



Abstract:Forecasting natural gas demand is a key problem for energy providers, as it allows for efficient pipe reservation and power plant allocation, and enables effective price forecasting. We propose a study of Italian gas demand, with particular focus on industrial and thermoelectric components. To the best of our knowledge, this is the first work about these topics. After a preliminary discussion on the characteristics of gas demand, we apply several statistical learning models to perform day-ahead forecasting, including regularized linear models, random forest, support vector regression and neural networks. Moreover, we introduce four simple ensemble models and we compare their performance with the one of basic forecasters. The out-of-sample Mean Absolute Error (MAE) achieved on 2017 by our best ensemble model is 5.16 Millions of Standard Cubic Meters (MSCM), lower than 9.57 MSCM obtained by the predictions issued by SNAM, the Italian Transmission System Operator (TSO).
Italian residential gas demand forecasting
Jan 04, 2019



Abstract:Natural gas is one of the most important energy sources in Italy: it fuels thermoelectric power plants, industrial facilities and domestic heating. Forecasting gas demand is a critical process for each energy provider, as it enables pipe reservation and stock planning. In this paper, we address the problem of short-term forecasting of residential gas demand, by comparing several statistical learning models, including Ridge Regression, Gaussian Processes, and Deep Neural Networks. We also present the preliminary steps of preprocessing and feature engineering. To the best of our knowledge, no benchmark is available for the task we performed, thus we derive a theoretical performance limit, based on the inaccuracy of meteorological forecasts. Our best model, a deep neural network, achieves an RMSE which is about double with respect to the performance limit.
Regularized linear system identification using atomic, nuclear and kernel-based norms: the role of the stability constraint
Jul 02, 2015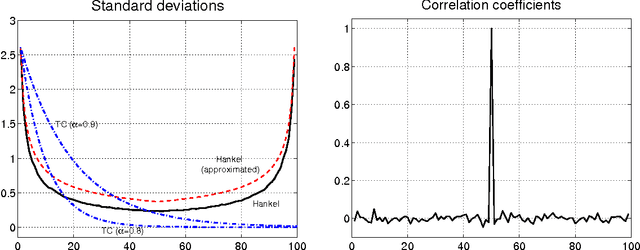
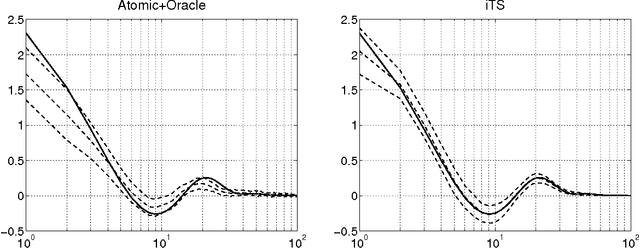


Abstract:Inspired by ideas taken from the machine learning literature, new regularization techniques have been recently introduced in linear system identification. In particular, all the adopted estimators solve a regularized least squares problem, differing in the nature of the penalty term assigned to the impulse response. Popular choices include atomic and nuclear norms (applied to Hankel matrices) as well as norms induced by the so called stable spline kernels. In this paper, a comparative study of estimators based on these different types of regularizers is reported. Our findings reveal that stable spline kernels outperform approaches based on atomic and nuclear norms since they suitably embed information on impulse response stability and smoothness. This point is illustrated using the Bayesian interpretation of regularization. We also design a new class of regularizers defined by "integral" versions of stable spline/TC kernels. Under quite realistic experimental conditions, the new estimators outperform classical prediction error methods also when the latter are equipped with an oracle for model order selection.
Efficient Marginal Likelihood Computation for Gaussian Process Regression
Oct 29, 2011


Abstract:In a Bayesian learning setting, the posterior distribution of a predictive model arises from a trade-off between its prior distribution and the conditional likelihood of observed data. Such distribution functions usually rely on additional hyperparameters which need to be tuned in order to achieve optimum predictive performance; this operation can be efficiently performed in an Empirical Bayes fashion by maximizing the posterior marginal likelihood of the observed data. Since the score function of this optimization problem is in general characterized by the presence of local optima, it is necessary to resort to global optimization strategies, which require a large number of function evaluations. Given that the evaluation is usually computationally intensive and badly scaled with respect to the dataset size, the maximum number of observations that can be treated simultaneously is quite limited. In this paper, we consider the case of hyperparameter tuning in Gaussian process regression. A straightforward implementation of the posterior log-likelihood for this model requires O(N^3) operations for every iteration of the optimization procedure, where N is the number of examples in the input dataset. We derive a novel set of identities that allow, after an initial overhead of O(N^3), the evaluation of the score function, as well as the Jacobian and Hessian matrices, in O(N) operations. We prove how the proposed identities, that follow from the eigendecomposition of the kernel matrix, yield a reduction of several orders of magnitude in the computation time for the hyperparameter optimization problem. Notably, the proposed solution provides computational advantages even with respect to state of the art approximations that rely on sparse kernel matrices.
Client-server multi-task learning from distributed datasets
Jan 11, 2010



Abstract:A client-server architecture to simultaneously solve multiple learning tasks from distributed datasets is described. In such architecture, each client is associated with an individual learning task and the associated dataset of examples. The goal of the architecture is to perform information fusion from multiple datasets while preserving privacy of individual data. The role of the server is to collect data in real-time from the clients and codify the information in a common database. The information coded in this database can be used by all the clients to solve their individual learning task, so that each client can exploit the informative content of all the datasets without actually having access to private data of others. The proposed algorithmic framework, based on regularization theory and kernel methods, uses a suitable class of mixed effect kernels. The new method is illustrated through a simulated music recommendation system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge